回归分析在超精密加工表面粗糙度预测中的应用

杨晓东YANG Xiao-dong

（黑龙江科技大学，哈尔滨 150022）

（Heilongjiang University of Science &Technology，Harbin 150022，China）

0 引言

由于在对KDP 这样的软脆单晶材料进行研磨和抛光的加工过程中能够十分便捷的嵌入晶体，但是却很难采用精密抛光的方法从晶体表面去除杂质，并且亚表层在抛光的过程中很容易造成损伤，这些杂质或缺陷成为零件激光损伤的来源并且这对高功率激光的应用是不能够忍受的，因此，要想采用传统的研磨和抛光方法将KDP 晶体加工出超光滑表面具有一定的难度。目前，对此类零件进行加工的时候，国内外普遍采用单点金刚石切削（SPDT）的方式。由于采用“飞刀”的切削方式容易在加工表面形成刀痕而在晶体透射波前增加小尺度的周期扰动。本次实验将重点研究已加工表面粗糙度受到切削速度（转数）、背吃刀量以及进给量（进刀速度）等切削用量的影响。

1 因素水平编码表的编制

因子xj（j=1，2，3）为坐标轴构成的空间称为因子空间。在因子空间寻找能够使表面粗糙度达到最小值的最优解即寻找最优化切削条件。本文采用了三因素二次回归通用旋转组合设计，表1 为各个因素的水平编码。对独立变量z1、z2、z3进行线性变换后，就建立起了n、f、ap与z1、z2、z3取值的一一对应关系。

表1 因素水平编码表

2 回归系数的计算及回归方程的求解

当有p 个变量时，二次回归方程的一般形式为

首先要确定各个回归系数，回归系数的计算公式如下：

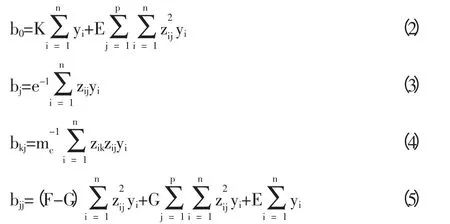
实验采用二次回归通用旋转组合设计，其实测值和预测值见表。当p=3，由表查得K=0.1663402，E=-0.056792，F=0.06939，G=0.00689003，e-1=0.07322，。KDP 晶体加工表面粗糙度预测模型可表示为

n、f、ap与z1、z2、z3值的对应关系可表示为

其约束条件为

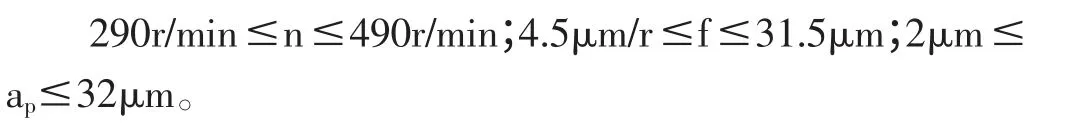
3 切削参数的优选及实验验证

由于采用解析法和通过大量实现来寻找表面粗糙度这一目标函数最小切削参数的最佳组合既麻烦又不现实，因此，我们利用了MATLAB 优化软件这个工具。由于在优化KDP 晶体超细精密加工表面粗糙度预测模型的时候，利用MATLAB 优化软件不需要考虑加工效率，而只需要考虑约束条件，因此能够迅速得到切削参数的最佳组合。经计算优选出的切削参数为：n=390r/min，f=10μm/r，ap=32μm。此时求得的KDP 晶体超精密加工表面粗糙度最优值为Ra=8.5611nm。

在上述条件下进行加工的表面实际测量值Ra=7.37nm。从测量值和预测值的一致性我们可以认为建立的预测模式是可靠有效的。

4 结论

由于本文采用回归分析法建立的预测模型能够通过较少的实验获得大量的信息，因此具有较高的数学模型效率。此外，对于模型的切削参数还可以利用优化软件进行优化。但是，在对加工表面粗糙度进行测量的时候，建立的预测模型受到随机误差的影响也会产生一定的误差，因此，为了解决这个问题，除了在测量表面粗糙度的时候使用分辨率较高的仪器外，还对每个观测值经过多次测量后经平均求得。

[1]杨福兴.激光核聚变光学元件超精密加工技术研究[J].光学技术，2003，29（6）:649-651.

[2]杨福兴.KDP 晶体超精密加工技术的研究[J].制造技术与机床，2003（9）：63-65.

[3]张文生，张飞虎，等.光学脆性材料的金刚石切削加工[J].光学精密工程，2003，11（2）：139-143.

[4]姜启源.数学模型[M].高等教育出版社，2003.