大跨度斜拉桥可靠度评估方法研究*

陈铁冰

（深圳职业技术学院 建筑与环境工程学院，广东 深圳 518055）

大跨度斜拉桥是一种缆索承重桥梁，结构较柔，几何非线性效应比较明显，同时在施工和营运过程中将面临主梁压曲、桥塔稳定和结构整体失稳等安全性问题，其材料、几何尺寸、外部荷载等随机因素对结构安全性影响尤为突出．因此，考虑随机变量的不确定性，进行大跨度斜拉桥可靠度评估具有十分重要的意义．

国内外学者采用各种方法对斜拉桥可靠度评估开展了大量研究工作．一次二阶矩法[1]计算结构可靠度简便、实用性强，但是需要显式表达结构极限状态方程．Monte Carlo法[2-3]进行随机抽样时，需要用结构有限元分析程序进行成千上万次计算，因此，对于大型复杂桥梁结构可靠度评估来说，该法不适用．响应面法[4-5]采用多项式近似地重构极限状态方程，但是其拟合函数是固定不可调的，而且结果受设计点位置的影响，用极限状态方程表达的曲面，对于大型复杂结构来说，非线性程度会很高，因此，在整个随机空间内对非线性极限状态曲面进行有效地模拟是非常困难的．随机有限元法[6]是通过级数展开和矩估计的摄动分析方法，当结构系统的失效曲面与随机参数构成的多维曲面有较大偏离时，计算误差将会显著增大．当极限状态方程可以显式表达时，将遗传算法、神经网络和响应面法[7]结合能够有效地评估斜拉桥可靠度．神经网络与Monte Carlo法[8]结合评估斜拉桥可靠度时，由于设计点位置未知，在随机变量的均值附近进行随机抽样，所训练的神经网络有效地模拟极限状态曲面具有一定的困难．对于斜拉桥结构体系可靠度评估，遗传算法、改进的β约界法能够有效地判别主要失效模式，并评估体系可靠度[9-11]．

本文提出了基于神经网络的大跨度斜拉桥可靠度评估方法．该方法采用Latin hypercube抽样技术[12]在整个定义域内对随机参数进行随机抽样，应用大跨度斜拉桥非线性有限元分析软件进行分析计算．通过对随机抽样的样本数据进行训练，应用神经网络的非线性映射和泛化技术，建立了桥梁结构响应与随机参数之间的非线性映射关系，利用训练好的神经网络模拟斜拉桥极限状态方程．通过极限状态方程对随机变量的偏导数，求解在标准正态空间坐标系中原点到极限状态曲面的最短距离优化问题，计算大跨度斜拉桥的可靠指标．

1 神经网络

1.1 BP神经网络

BP神经网络由2部分构成，正向传播和反向传播[13]，其结构由输入层、隐含层和输出层等三层组成，如图1所示．

各种随机变量作为输入层与隐含层神经元之间的关系[13]为

式中，x表示随机变量向量；θ表示阈值向量；w表示权值向量；y表示隐含层的神经元．

可以采用式（2）表达的对数S型（log-sigmoid）函数[13]作为激活函数，

隐含层神经元与表达极限状态方程值的输出层之间采用线性函数来表达，如式（3）[13]所示，

式中，v表示权值向量；η表示阈值向量；z表示输出层神经元．

通过公式（1）～（3）可以看出，表达随机变量的输入层与隐含层之间的激活函数，以及隐含层与表达极限状态方程值的输出层之间的激活函数都能够用显式的方式进行表达，因此就能够应用上述公式对各种结构随机变量与极限状态方程值之间的函数关系进行显式表达．

1.2 归一化

利用神经网络进行训练时，由于各随机变量的单位和大小可能不同，如果直接进行训练，会造成数据失真，可以采用公式（4）对数据进行归一化处理来避免数据失真，

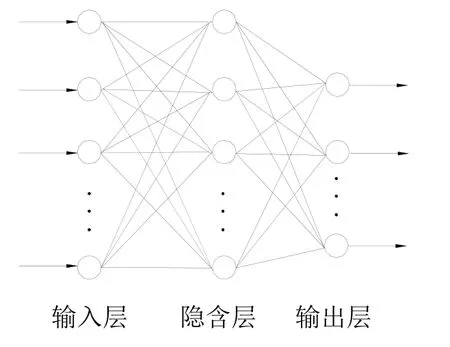
图1 BP神经网络结构

1.3 Latin hypercube抽样

神经网络训练时样本如何抽取是一个重要的问题．目前基于神经网络的结构可靠度评估研究中，通常按照工程 3σ原则在随机变量的限定区域中采用均匀抽样法抽取训练样本[8]．但是，采用上述抽样策略不能保证所抽取的训练样本位于随机变量的整个定义域内．Latin hypercube抽样[12]是一种高效的小样本抽样技术，能给出无偏或偏度很小的随机变量估值，其方差也较简单的随机抽样显著减小．

根据Latin hypercube抽样的基本原理，对于K个随机变量X，具有已知分布函数Fkx，k＝1，2，…，K．将随机变量kx在定义域内划分为N个等概率区域．对于第i个区间（i＝1，2，…，N），随机变量xk的累积概率Pi由公式（5）[12]计算

其中，ru表示0到1区间内的均匀随机数．

随机变量xk的第i个抽样为

2 基于神经网络的大跨度斜拉桥可靠度评估方法

2.1 结构可靠指标计算的优化模型

对于有n个随机变量的结构来说，标准正态空间坐标系中原点到极限状态曲面的最短距离就是结构可靠指标 β[15]．因此，求解结构可靠指标为一个优化问题，可以用式（7）[15]建立结构可靠指标计算的优化模型，

式中，经过标准正态化处理后，正态随机变量 x变为x′．可以采用迭代算法对公式（7）进行求解，如公式（8）[15]所示

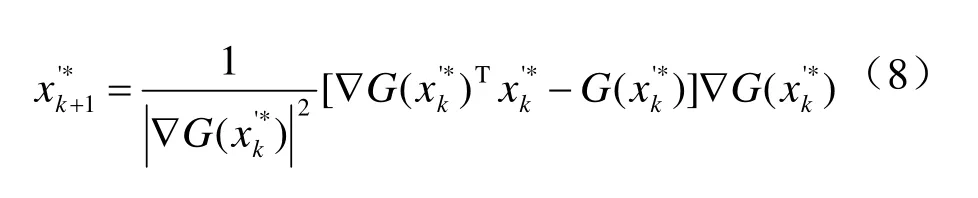
对于大跨度斜拉桥来说，公式（7）中的第二式所表示的极限状态方程一般难以显式表达，同时也无法计算公式（8）中极限状态方程对各随机变量的偏导数，因此难以通过迭代的方法求解设计点，也无法通过公式（7）的第一式计算可靠指标 β．如前所述，基于神经网络技术，应用公式（1）～（3），能够将各随机变量x与极限状态方程值z之间的函数关系显式表达出来，因此，当计算出极限状态方程对各随机变量的偏导数后，就能够通过迭代算法求解公式（7）和（8），从而计算出结构可靠指标值．

2.2 偏导数计算

公式（2）中对数S型函数的导数为

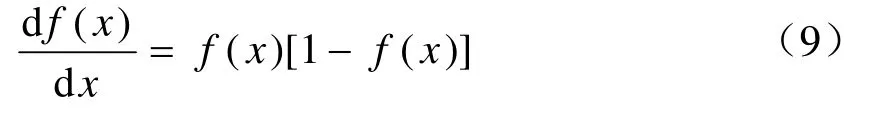
则根据公式（1）～（4）以及（9），按照链式法则，极限状态方程值z对随机变量xi的偏导数为

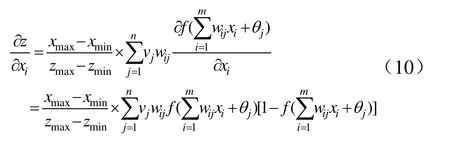
假定初始设计点 xk'*后，就可通过公式（1）～（4）、（7）～（10）计算新的设计点xk'*+1和可靠指标β．

3 计算流程

应用前述的方法，可以采用如下流程计算大跨度斜拉桥可靠指标值：

1）给出迭代计算时的精度，对随机变量x的统计特征和分布类型进行假定，并将各随机变量的均值作为设计点的初值，x*＝x1，x2，…，xn．

2）对非正态分布变量进行当量正态化变换处理．将设计点变换到标准正态分布空间中．

3）应用前述Latin hypercube抽样技术构造随机变量x*训练样本．输入值采用随机变量x*训练样本，输出值为大跨度斜拉桥非线性有限元程序计算的结构响应值．采用归一化技术进行数据处理．对公式（1）和（3）中三层权值和阈值进行初始化处理，应用Lenvenberg－Marquardt算法对神经网络进行训练，能够计算得到三层神经网络的权值和阈值．应用经过训练的神经网络，在设计点处应用公式（10）计算极限状态方程对随机变量的偏导数，并计算极限状态方程值[14]．

5）在原坐标空间内，应用新的设计点来计算极限状态方程值g(x*），同时对迭代前后两次β的差值Δβ进行计算．当g(x*）和Δβ均小于步骤1)指定的迭代精度时，则迭代计算停止，否则，从步骤 2)重新开始计算，当满足收敛条件时，迭代计算停止．

基于Microsoft Fortran Powerstation 4.0平台，应用上述计算流程，编制了Fortran计算程序，可以进行大跨度斜拉桥可靠度评估．

4 实例分析

首先，进行平面框架结构可靠度评估，研究Latin hypercube抽样的性能、计算精度、隐式极限状态方程模拟、计算效率等内容，通过与其它方法对比，考察所建立方法的特点．其次，对南京二桥可靠度评估，考察两种规范布载、车道荷载布载方式、几何非线性效应等内容，研究大跨度斜拉桥可靠度的特性．

4.1 平面框架结构可靠度评估

选取三跨十二层建筑的平面框架进行分析计算，结构计算简图[16]如图2所示．

各个杆件的弹性模量均为E=2.0´107kN·m-2．用表达截面惯性矩和截面面积之间的关系，各杆件截面积及外荷载P的统计特征见表1．

在正常使用极限状态下，极限状态方程[16]为

图2 平面框架结构计算简图（单位：m）

其中：表示uA表示节点A的水平位移，单位m．

采用Latin hypercube抽样进行计算，将计算结果与响应面法和重要抽样法对比见图3．通过图3可以看出，Latin hypercube抽样数目取为10～40，结构失效概率大致在7.309´10-2[16]（响应面法）和7.506´10-2[16]（重要抽样法模拟2000次）之间．说明采用Latin hypercube抽取小样本，应用本文方法计算结构失效概率具有很高的精度．

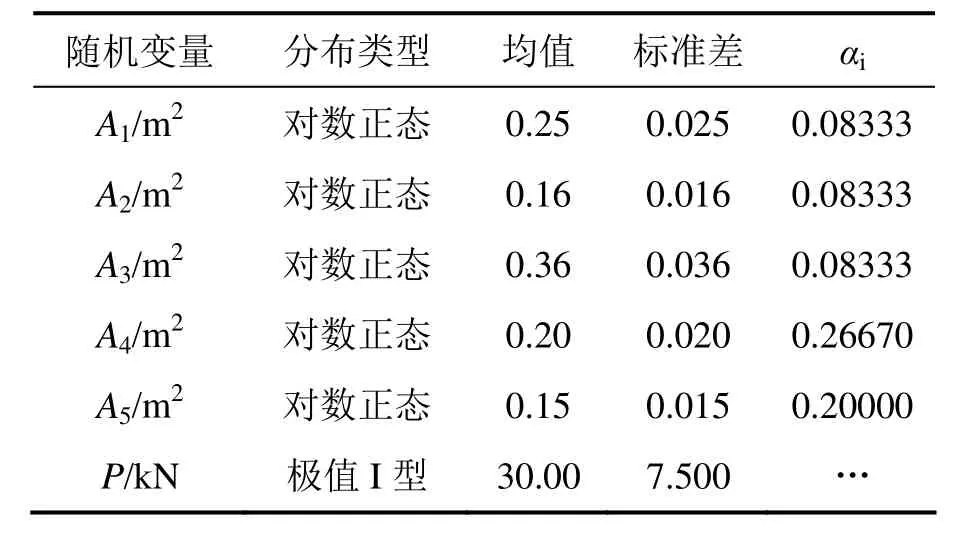
表1 随机变量统计特征

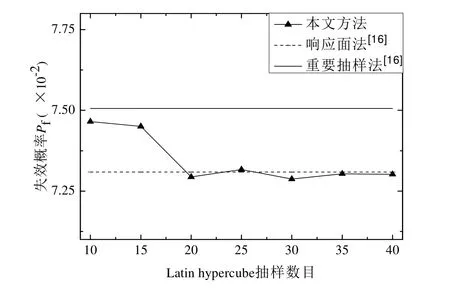
图3 3种方法计算结构失效概率

当Latin hypercube抽样数目分别为10、15和20时，用表2表示本文的计算结果与重要抽样法和响应面法的对比．能够看出，在设计点、可靠指标、失效概率等方面，本文的计算结果与响应面法吻合的很好．通过与响应面法进行对比，可以发现本文是直接利用结构有限元分析程序进行计算，利用神经网络的非线性映射能力对极限状态方程进行模拟，通用性能比较好．与重要抽样法进行对比，在计算精度一定时，结构有限元分析计算的次数减少了很多，计算效率得到提高．

4.2 南京二桥结构可靠度评估

4.2.1 计算模型

南京长江二桥南汊大桥为双塔斜索面钢箱梁斜拉桥．跨度布置为（58.5+246.5+628+246.5+58.5）m．斜拉索采用扇形布置，20对斜拉索组成一个索面，标准索距为15m．桥塔采用混凝土结构，塔高 195m．主梁为带风嘴的闭合钢箱梁，主梁宽度37.2m，梁高3.5m．图4表示计算简图．

大跨度斜拉桥的几何非线性效应非常明显．大跨度斜拉桥包括斜拉索垂度效应、梁柱效应及大位移效应等3个方面的几何非线性效应[4]．考虑斜拉桥几何非线性效应并采用形状迭代确定斜拉桥成桥恒载初始索力，有关方法及结果验证见文献[4]．

假定南京二桥结构随机变量分别为梁﹑塔﹑索的弹性模量Ei﹑截面面积Ai﹑抗弯惯矩Ii﹑材料容重gi、公路－I级车道荷载及汽超-20轴重Pi等，共26个随机变量．统计特征见表3．

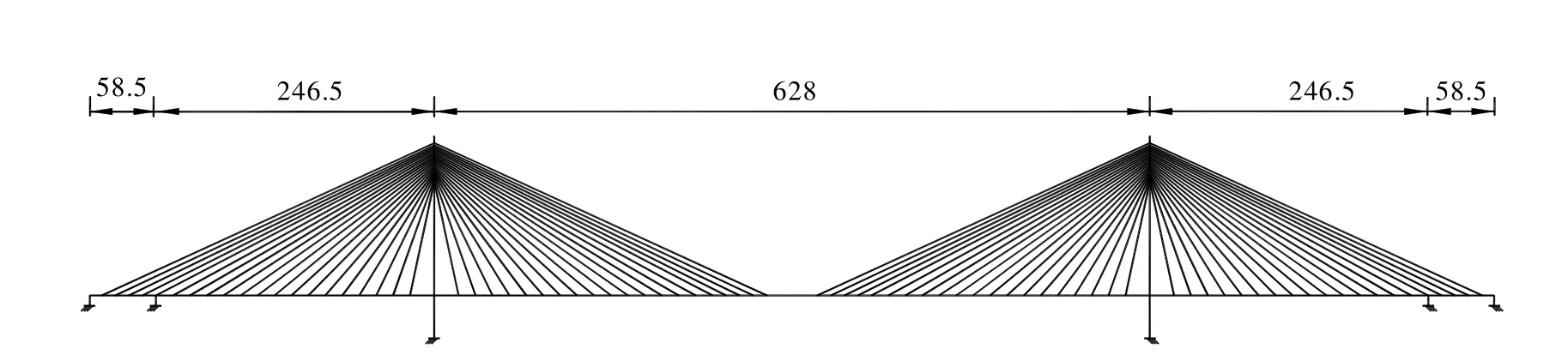
图4 南京二桥南汊大桥主桥结构计算简图（单位：m）

表2 3种方法计算结果对比

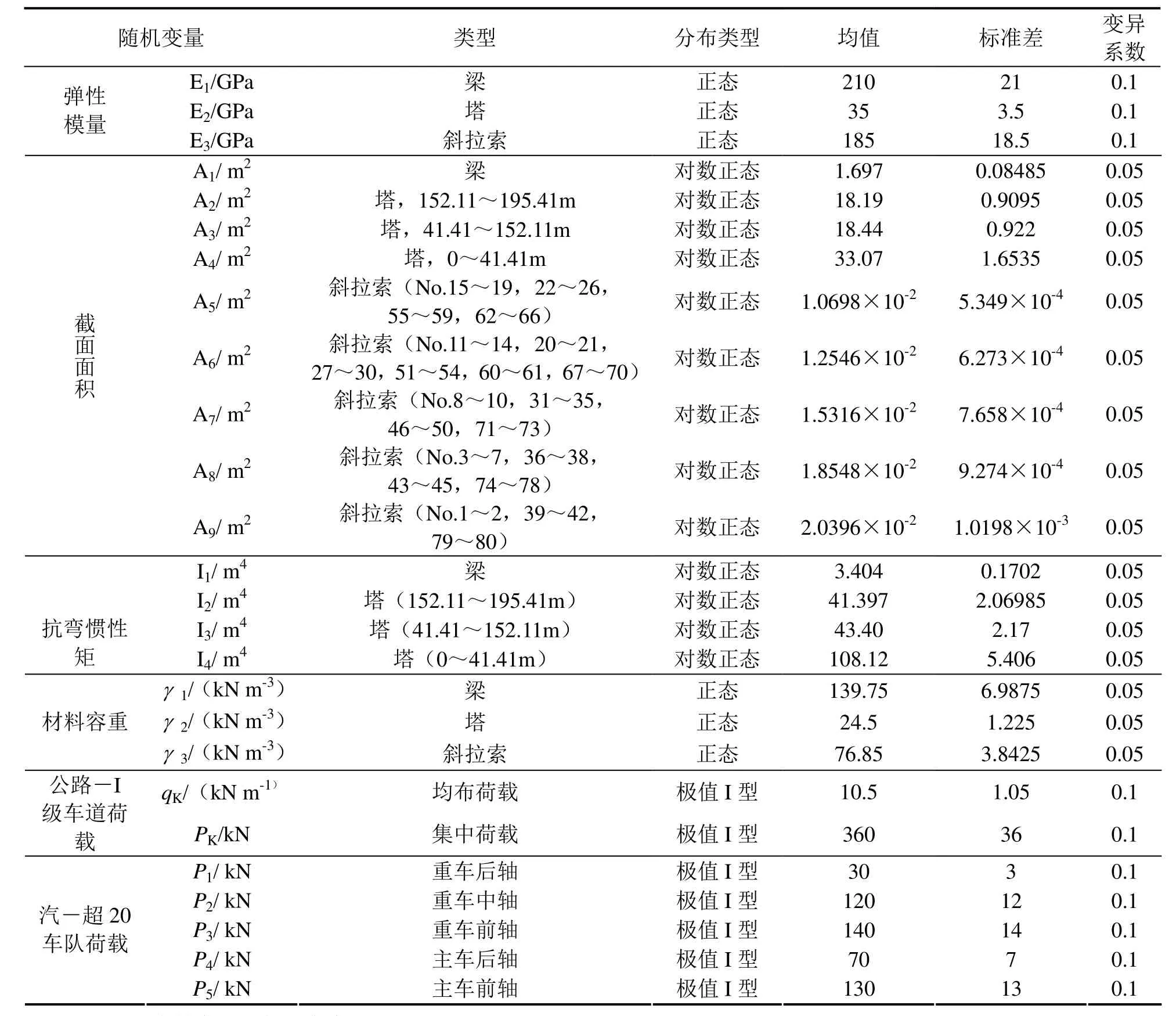
表3 南京二桥随机变量统计特征

4.2.2 采用2种规范布载的斜拉桥可靠度评估

活载按规范 JTG D60－2004[17]的公路－I级车道荷载（以下简称车道荷载）和规范 JTJ 021－89[18]的汽－超 20车队荷载（以下简称车队荷载）2种工况进行考虑，荷载布置方式如图5所示，随机变量统计特征见表3．

根据规范JTJ 027－96[19]，，主梁在正常使用极限状态下时汽车荷载（不计冲击力）作用下的最大竖向挠度为[u]=L/400 =628/400=1.57m（L为中跨跨径），极限状态方程

其中，结构响应uV为中跨跨中竖向挠度．

2组工况的活载横向布置按6车道或车队布载，纵向布置采用中跨布载和全桥布载两种方式，其中车道荷载的集中荷载作用在中跨跨中位置，车队荷载的重车前轴作用在中跨跨中位置，横向折减系数为0.55，纵向折减系数为0.95．将表3中其它随机变量的统计特征保持不变，改变车道和车队荷载的标准差和变异系数，考察斜拉桥可靠指标的变化，Latin hypercube抽样数目取为80．计算结果对比见图6．

由图6可以看出，无论是公路－I级车道荷载还是汽－超20车队荷载，荷载中跨布置时可靠指标均小于全桥布置时可靠指标，说明荷载布置方式对斜拉桥可靠指标有很大影响，与全桥布置荷载相比，中跨布置荷载将显著降低斜拉桥的安全性．当荷载变异系数增大时，车道荷载布载时可靠指标小于车队荷载布载时可靠指标，说明与车队荷载布载相比，车道荷载布载时斜拉桥偏于不安全．当荷载变异系数小于 5%，荷载中跨布置或全桥布置时，车道荷载与车辆荷载的布载相比，可靠指标大致相等．随着荷载变异系数的增大，车道荷载布载时可靠指标逐渐减小．荷载变异系数的变化对车队荷载布载时可靠指标的影响很小．主要原因是车道荷载由均布荷载和一个集中荷载组成，且集中荷载均值较大，集中荷载作用于中跨跨中时对斜拉桥的作用效应较大，因此，当均布荷载和集中荷载变异增大时对斜拉桥可靠度会有显著影响．而车队荷载由重车和主车组成，按车队纵向排列于斜拉桥上，对结构的作用效应比较均匀，因此，对于车队荷载布载来说，当荷载变异系数增大时对斜拉桥可靠度影响较小．

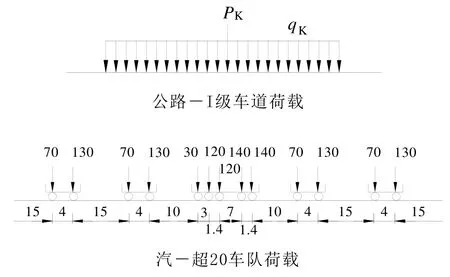
图5 两种规范的活载布置方式

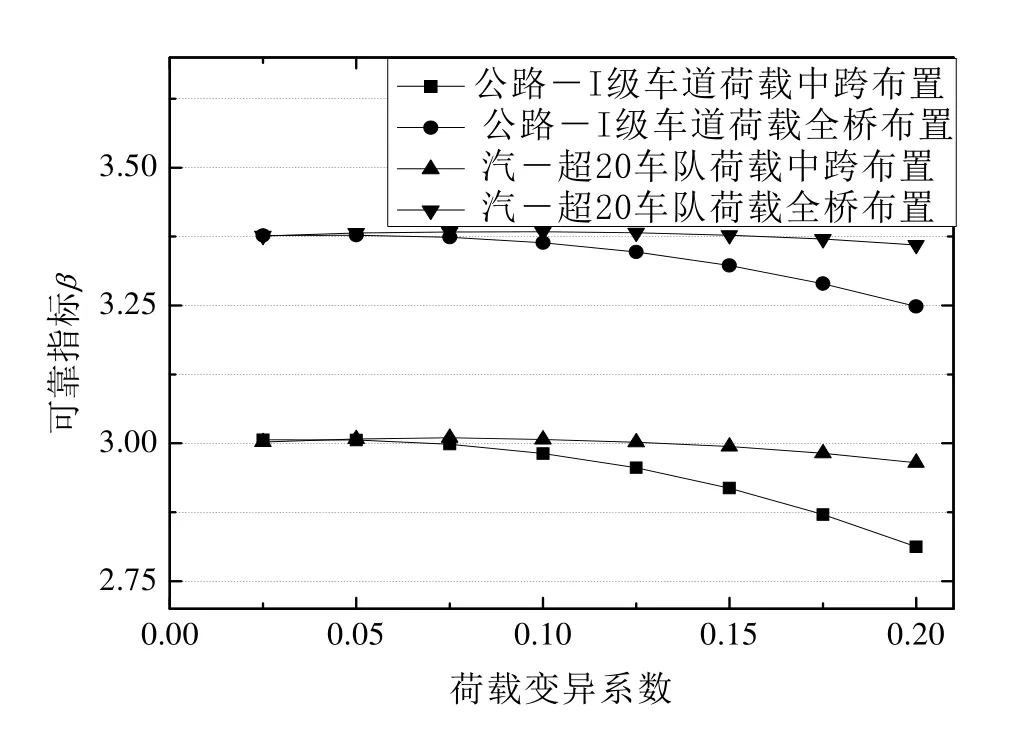
图6 荷载变异时可靠指标的变化

4.2.3 公路－I级车道荷载布载方式对斜拉桥可靠度的影响

公路－I级车道荷载中的均布荷载布置于中跨，集中荷载分别布置于中跨的跨中、3/8、1/4和 1/8跨等点．将公式（12）极限状态方程中的结构响应uV分别取为中跨跨中、3/8、1/4和1/8跨等点的竖向挠度．考察集中荷载位置变化对斜拉桥各点可靠度的影响，计算结果见图7．

通过图7可以看出，公路－I级车道荷载中集中荷载的作用位置对斜拉桥各点可靠指标有很大影响，集中荷载作用于中跨跨中时为全桥最不利位置，此时斜拉桥中跨跨中的可靠指标最小．集中荷载作用于斜拉桥某一点时，对各点的可靠指标影响程度不同，对于该作用点的可靠指标影响最大，对其它点的可靠指标影响较小．随荷载变异系数的增大，斜拉桥可靠指标均减小．

4.2.4 几何非线性效应对斜拉桥可靠度的影响

公路－I级车道荷载中的均布荷载布置于中跨，集中荷载布置于中跨跨中．为了全面考察几何非线性效应对斜拉桥可靠度的影响，采用不计入几何非线性效应、仅考虑斜拉索垂度效应、仅考虑梁柱效应及大位移效应、计入三种几何非线性效应等方式计算斜拉桥可靠指标，结果见表4．

通过表4可以看出，与不计入几何非线性效应相比，计入几何非线性效应后斜拉桥可靠指标大大减小，说明几何非线性效应对大跨度斜拉桥可靠度有显著影响，不计入几何非线性效应，斜拉桥将偏于不安全．在三种几何非线性效应中，斜拉索垂度效应对大跨度斜拉桥可靠度的影响最为显著，梁柱及大位移效应影响很小．

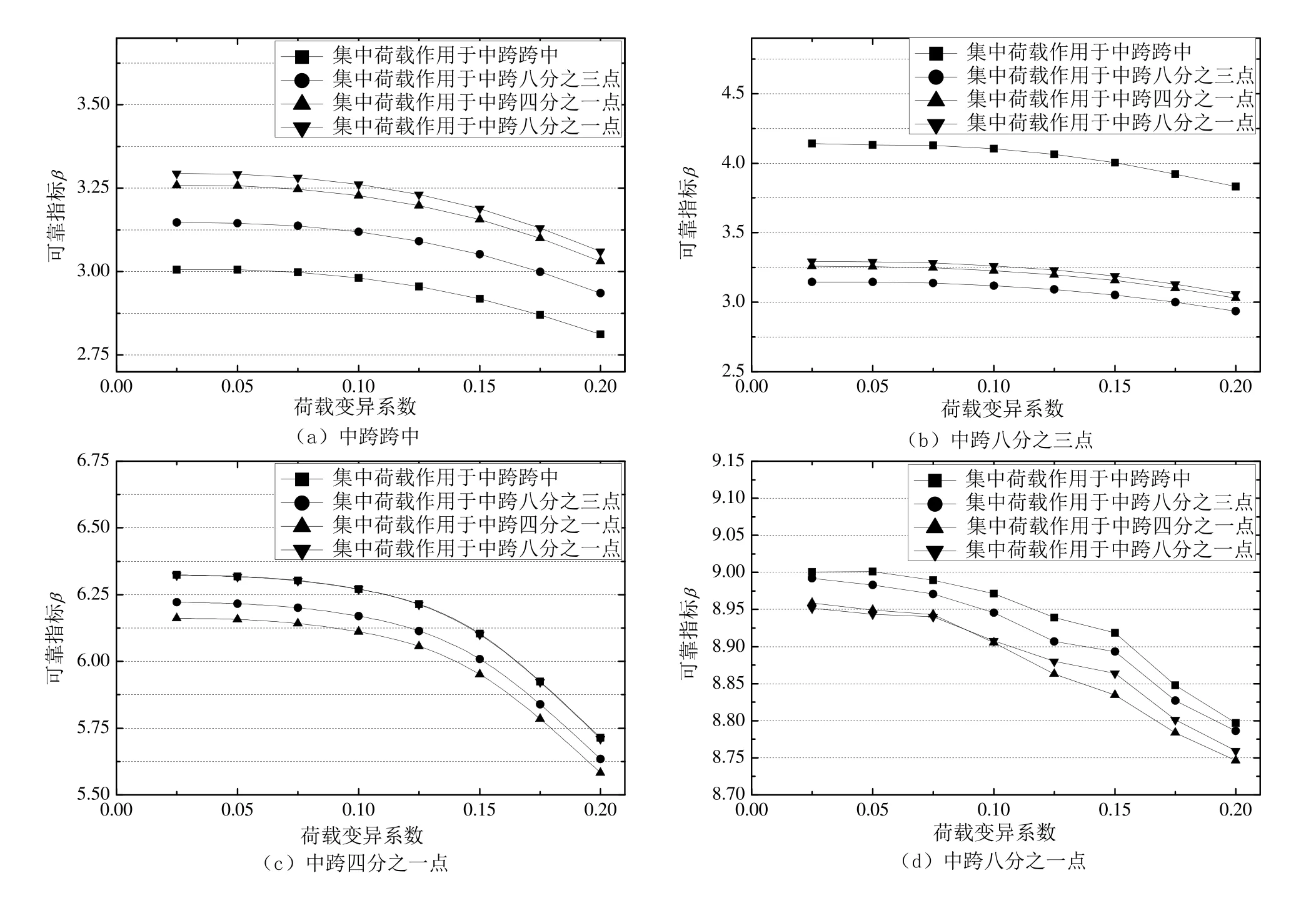
图7 集中荷载位置变化对斜拉桥各点可靠指标的影响

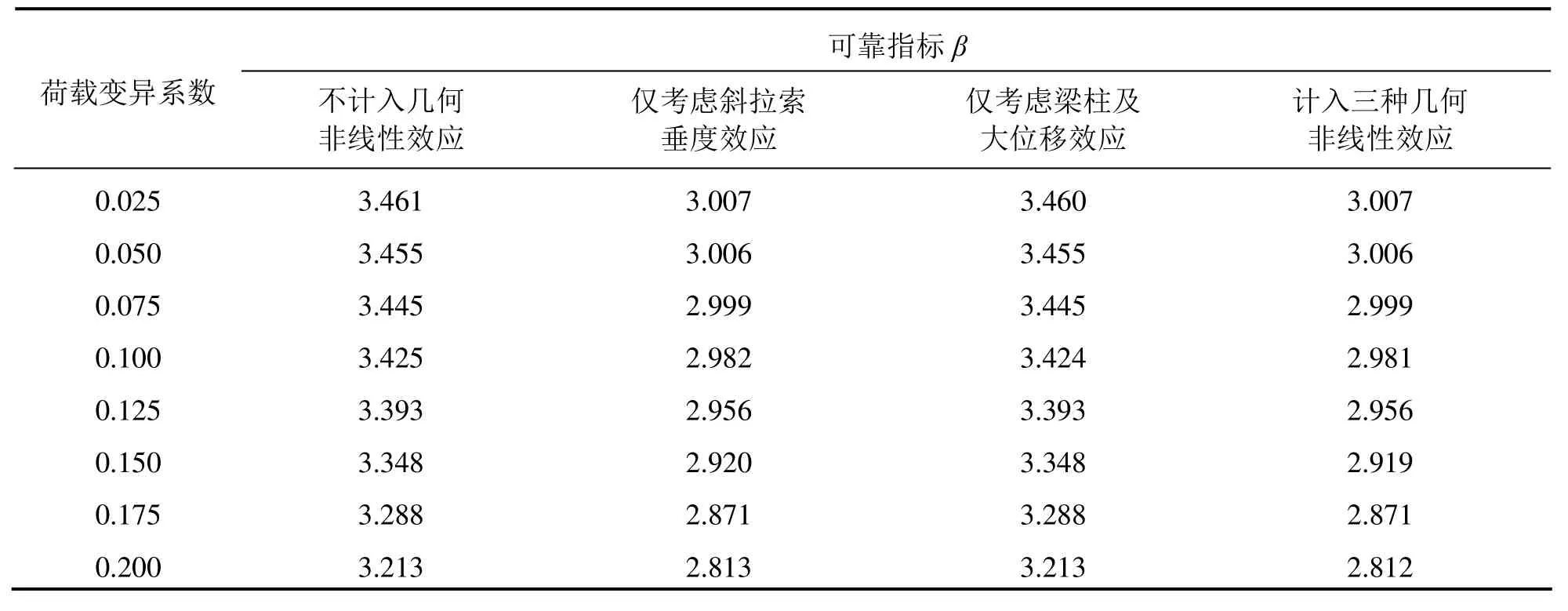
表4 几何非线性效应对斜拉桥可靠指标的影响

5 结 论

1）提出了基于神经网络的大跨度斜拉桥可靠度评估方法．该方法通过Latin hypercube抽样技术对随机参数进行抽样，应用大跨度斜拉桥非线性有限元进行分析．通过对随机抽样的样本数据进行训练，应用神经网络的非线性映射和泛化技术，对大跨度斜拉桥的极限状态方程进行数值模拟．通过极限状态方程对随机变量的偏导数，求解结构可靠指标的优化问题，计算大跨度斜拉桥的可靠指标．

2）研究结果表明，所建立的方法计算结构失效概率具有很高的精度，应用大跨度斜拉桥结构非线性有限元程序进行分析计算，利用神经网络的非线性映射能力对极限状态方程进行模拟，通用性能比较好，调用结构有限元分析计算的次数减少了很多，计算效率得到提高．

3）荷载布置方式对斜拉桥可靠指标有很大影响，与全桥布置荷载相比，中跨布置荷载将显著降低斜拉桥的安全性．与汽－超20车队荷载布载相比，公路－I级车道荷载布载时斜拉桥偏于不安全．

4）公路－I级车道荷载中集中荷载的作用位置对斜拉桥各点可靠指标有很大影响，集中荷载作用于中跨跨中时为全桥最不利位置，斜拉桥中跨跨中的可靠指标最小．随荷载变异系数的增大，斜拉桥可靠指标均减小．

5）计入几何非线性效应后斜拉桥偏于不安全．在三种几何非线性效应中，斜拉索垂度效应对大跨度斜拉桥可靠度的影响最为显著，梁柱及大位移效应影响很小．

[1] BRUNEAU M. Evalution of system - reliability methods for cable -stayed bridge design[J]．Journal of Structure Engineering, 1992，118（4）：1106-1120．

[2] FLORIAN A，NAVRATIL J. Reliability analysis of the cable - stayed bridge in construction and service stages[C]//Proceeding of the 6th ICOSSAR,Rotterdam: Belkema, 1993：869-877．

[3] CHO H N, LIM J K, PARK K H. System reliability and system reliability-based carrying capacity evaluation of cable-stayed bridges[C]// Proceeding of the 7th ICOSSAR, Rotterdam: Belkema, 1997：1927-1934．

[4] 陈铁冰，王书庆，石志源．计入结构几何非线性影响时斜拉桥可靠度分析[J]．同济大学学报，2000，28（4）：407-412．

[5] 程进，肖汝诚．斜拉桥结构静力可靠度分析[J]．同济大学学报，2004，32（12）：1593-1598．

[6] FRANGOPOL D M, IMAI K. Reliability of long span bridges based on design experience with the Honshu-Shikoku bridges[J]．Journal of Construction Steel Research, 2004，60（3-5）：373-392．

[7] 张建仁，刘扬．遗传算法和人工神经网络在斜拉桥可靠度分析中的应用[J]．土木工程学报，2001，34（1）：7-13．

[8] 朱劲松，肖汝诚，何立志．大跨度斜拉桥智能可靠度评估方法研究[J]．土木工程学报，2007，40（5）：41-48．

[9] WANG J, GHOSN M. Hybrid data mining/genetic shredding algorithm for reliability assessment of structural systems[J]．Journal of Structural Engineering,2006，132（9）：1451-1460．

[10] 刘扬，张建仁．混凝土斜拉桥施工阶段的体系可靠度[J]．中国公路学报，2006，19（5）：53-58．

[11] CHOI H, LEE S, CHOI I, CHO H, MAHADEVAN S.Reliability-based failure cause assessment of collapsed bridge during construction[J]．Reliability Engineering and System Safety, 2006，91（6）：674-688．

[12] MCKAY M D, CONOVER W J, BECKMAN R J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]．Technometrics, 1979，21（2）：239-245．

[13] HAGAN M T, DEMUTH H B, BEALE M H. Neural network design[M]．Boston: PWS, 1996．

[14] 陈铁冰．基于神经网络重要抽样法的结构可靠度评估[J]．深圳职业技术学院学报，2009，8（3）：38-41．

[15] HALDAR A, MAHADEVAN S. Reliability assessment using stochastic element analysis[M]．New York: Wiley,2000．

[16] 赵国藩．工程结构可靠性理论与应用[M]．大连：大连理工大学出版社，1996．

[17] JTG D60－2004 公路桥涵设计通用规范[S]．北京：人民交通出版社，2004．

[18] JTJ 021－89 公路桥涵设计通用规范[S]．北京：人民交通出版社，1989．

[19] JTJ 027-96 公路斜拉桥设计规范（试行）[S]．北京：人民交通出版社，1996．