基于改进灰色模型电力负荷预测
刘基群LIU Ji-qun
(四川省内江市供电局,内江 641000)
(Neijiang City Power Supply Bureau of Sichuan,Neijiang 641000,China)
0 引言
负荷预测是电力系统安全、经济和可靠运行的基础,并且对国民经济也有重要的意义,因此,电力负荷预测理论与技术一直是国内外研究的重点[1-2]。目前国内外负荷预测领域中,传统的预测方法主要有:线性回归预测算法[3]、时间序列法[4]、灰色预测法。灰色系统(GS)是由邓聚龙在1982年原先创立的。灰色系统理论经过20 多年的发展,目前已经成为一门新兴的边缘学科,应用日益广泛。灰色系统理论主要解决少数据、小样本、信息不完全和经验缺乏的不确定性问题[5-6]。原始的灰色模型GM(1,1)模型存在许多局限性,因此,从灰色模型提出开始,就有大量学者对灰色模型进行改进。牛东晓等在其文献中介绍了通过改造初始条件对灰色模型进行优化的方法:指数加权法、滑动平均法、缓冲算子处理法等,取得良好的效果[1]。针对灰色模型的局限性,很多学者结合智能算法对其进行了改进,目前有与蚁群、粒子群优化、BP 神经网络、支持向量机等智能仿真算法相结合的灰色预测模型,并且广泛应用到实际负荷预测中[7][8]。基于智能算法对灰色模型的改进虽然取得了很好的效果,但是智能算法也存在着模型复杂度高、寻优不确定等缺点。本文运用指数加权法对初始数据进行处理,结合对初值x(1)(1)的改进,即利用预测值和实际值的欧氏距离最小化的方法来确定连续变化微分方程时间响应式中的参数c 值来代替x(1)(1),通过对多个预测年用电量的预测值与真实值之间的误差的计算,发现新模型的预测误差明显低于传统的GM(1,1)灰色模型,说明新模型对原模型有明显的改进效果。另外,改进后的新模型在算法实现方面并没有明显增加计算的复杂度,这又从另一个方面证实了该改进方案的有效性。
1 灰色系统的基本理论与预测模型
1.1 灰色电力负荷预测概述 电力负荷预测的实质是对电力市场的需求进行预测,它是电力系统规划的基础,作为衡量电力系统管理现代化的重要标志。准确预测未来城市对电力的需求量和未来城市电网的供电容量,对城市供电电源点的确定和发电规划具有重要的指导意义。灰色系统(GS)是由邓聚龙在1982年首先创立的。灰色系统理论经过20 多年的发展,目前已经成为一门新兴的边缘学科,应用日益广泛。灰色系统理论主要解决少数据、小样本、信息不完全和经验缺乏的不确定性问题,将其有用影响因素复杂、不确定性较强的电力负荷预测中有很高的理论和实际意义。
1.2 灰色建模过程
1.2.1 建立原始数列X(0)

1.2.2 建立累加生成数列X(1)
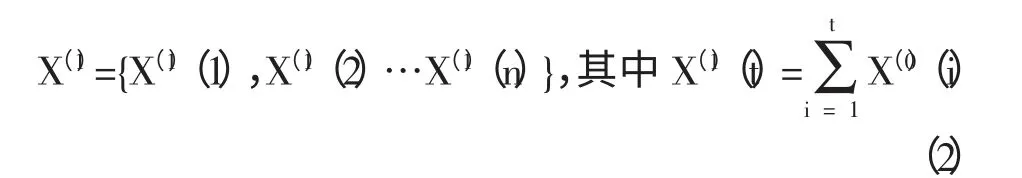
1.2.3 建立GM(1,1)模型的原始形式及微分方程
GM(1,1)模型的原始形式为:

其中a 为发展系数,b 为灰色作用量。
建立其一阶微分方程:


u 为协调系数。
1.2.4 确定方程参数 根据最小二乘原理求参数:

1.2.5 建立时间相应函数 通过上述计算,得到模型的时间响应函数:
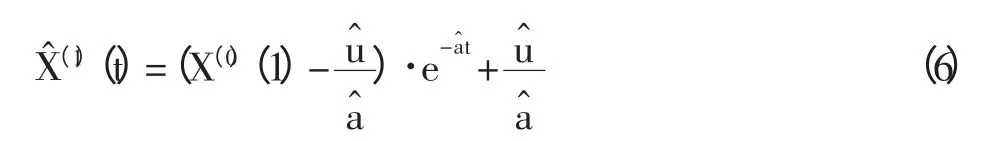
1.2.6 确定原始数值 对X^(1)进行累减生成计算,得到还原值:
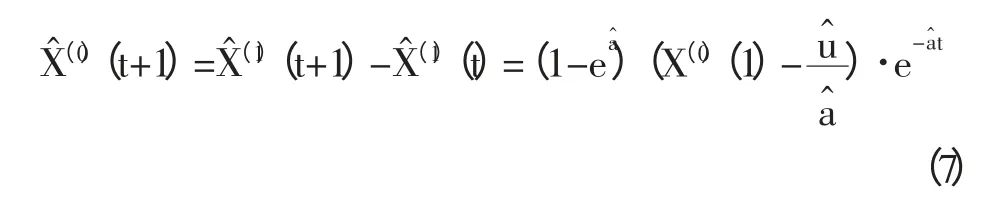
2 改进灰色模型电力负荷预测
2.1 GM(1,1)模型的局限性 GM(1,1)在许多领域尤其是数据缺乏和不确定性显著的状况中得到了广泛应用。但是由于GM(1,1)存在合理选择背景值、从微分离散方程求得参数直接带入到连续方程中的直接跳跃等模型本身存在固有的参数估计缺陷问题,模型预测值和实际值可能会存在较大误差,在进行实际电力负荷预测时具有以下局限性:
①传统GM(1,1)模型对数据要求比较高,当原始数据的离散程度较大时,会使得模型预测的不准确。
②灰色负荷预测适用于有少量历史负荷数据的系统,当原始数据量过大时,传统灰色模型便会表现出不适宜性。
③原始灰色预测模型对中长期的预测不是特别准确,可能出现增长率过快的情形。
④传统GM(1,1)模型仅考虑用电负荷这一单一的因素,而电力负荷往往会受到很多复杂因素的影响,并且该模型也不能在未来任何时刻都能充分反映电力负荷的发展趋势。
传统GM(1,1)模型的局限性导致其不能满足实际电力负荷预测应用的需要,因此需要对GM(1,1)模型进行改进,改善GM(1,1)模型的缺陷,从而提高其预测精度和模型实用性。
2.2 对初始条件的改进 由于电力负荷变化具有波动性,可能受到异常值的影响,对电力负荷原始数据序列进行处理需要强化原始数列的趋势,消弱异常值的影响,从而提高数据的使用效率,得到更精确的结果。指数加权法是负荷预测方法中使用的最普遍的一种方法,在实际中得到了较好的运用。对原始数列{x(0)(t)}按下式(令y(0)(1)=x(0)(1)):
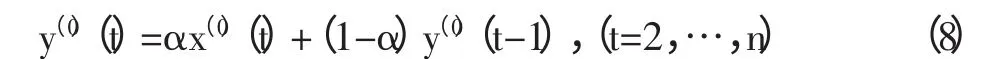
生成新的指数递增序列{y(0)(t)},注意要求{x(0)(t)}都为正。然后对{y(0)(t)}应用GM 方法进行预测,得预测值,再按下式:

将序列还原成{x(0)(t)}。
2.3 对初值选择的改进 在原始灰色模型GM(1,1)中,选取x(1)(1)作为初值,采用曲线拟合,根据初值求解时间响应式。然后x(1)(1)是一个最旧的历史数据,与未来关系并不密切,规律性较弱,这一点使得对初值的选取进行改进成为必要。
为了改进预测模型,提高预测精度,利用预测值和实际值的欧氏距离最小化的方法来确定连续变化微分方程时间响应式中的参数c 值,具体表示公式如下:
设微分方程如下:

则其通解为:

在传统GM(1,1)模型中,通过假使x(1)(1)=x(0)(1),得到

本文通过构造原始数据序列x(0)(k)与预测值x^(0)(k)的欧氏距离构成的函数F(c),求解该函数最小值:
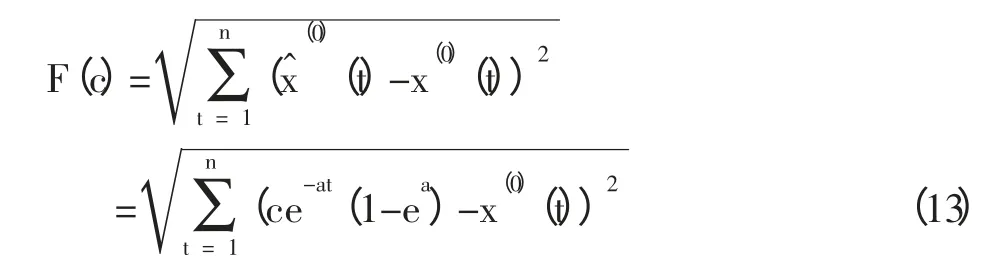
根据极值的一阶条件:令F(c)′=0,从而求得c 值。

将所求c 代入通解公式,便得到改进初值的灰色模型。在本文中,取x(0)(t)为平滑处理后的数据。
3 应用及算例结果分析
笔者通过统计年鉴中1999年到2005年的用电量预测2006年到2010年的用电量。将改进后的预测结果与实际值进行比较,求出绝对误差和相对误差,并且与普通的误差进行比较,用Matlab7.1 编程得到以下结果,如表1 所示。

表1 两种GM(1,1)模型的负荷预测与模拟误差比较
由结果可以看出,改进后的灰色GM(1,1)模型比原始灰色模型的预测准确度有很大提高,特别是对2年后数据的预测,相对误差降低了将近一半;改进前对未来5年负荷预测的平均相对误差为6.94%,改进后模型预测的平均相对误差为3.90%,误差率降低了3.04%;以上数据都表明本文对原始灰色模型的改进是有意义的,能取得比较好的效果。
4 总结与展望
随着电力改革的深入,电网建设的滞后性已成为制约经济社会发展的瓶颈,电网规划和电网建设成为今后电力企业工作的重心,这也决定了电力负荷的中长期预测的重要性。电力负荷的中长期预测是电网运行的经济性、安全性和可靠性的保证。本文主要用指数平均法和对初值的改进对原始灰色GM(1,1)模型进行了改进,通过用1999-2005年的我国年度电力消费量预测2006-2010年的年度电力消费量,并且与实际值进行对比,证明了对模型改进的有效性。
由本文中的预测结果可以看出,在进行电力负荷年度预测是,对前两年的预测精度是很高的,而对三年后的数据的预测就出现了较大的相对误差,而进行电网规划时有时需要对5年,10年后的负荷进行预测,因此本文的模型出现了很大的局限性,还需要对初始序列,初值,以至于模型本身进行进一步的改进才能更好的对长期负荷进行预测,对电力规划提供指导。
[1]牛东晓.电力负荷预测技术及其应用[M].北京:中国电力出版社,1998.
[2]牛东晓.具有二重趋势性的季节型电力负荷预测组合优化灰色神经网络模型[J].中国电机工程学报,2002,22(1):29-32.
[3]黄元生,王玉玮.基于线性回归方法的我国电力市场短期用电需求预测分析[J].价值工程,2011(11):17-18.
[4]Contreras J,Espinola R,Nogales F J,et al.ARIMA models to predict next-day electricity prices[J].IEEE Trans on Power Systems,2003,18(3):1014-1020.
[5]肖新平,宋中民,李峰.灰技术基础及其应用[M].科学出版社,2005.
[6]邓聚龙.灰色系统基本方法(第2 版)[M].华中科技大学出版社,2005:2-12.
[7]Che—Chiang Hsu,Chia -Yon CHEN.Applications of improved grey prediction model for power demand forecasting[J].Energy Conversion and management,2003(44):55-57.
[8]刘洪涛,肖广明,刘俊涛.基于粒子群优化灰色模型的电力系统负荷预测[J].东北电力大学学报,2009(2):69-72.

