不同尺寸混凝土楔入劈拉试件双K断裂韧度试验研究与理论分析

胡少伟，谢建锋

(1.南京水利科学研究院，江苏 南京210024;2.水文水资源与水利工程科学国家重点实验室，江苏 南京210024)

三点弯曲梁法和楔入劈拉法是《水工混凝土断裂试验规程》(DL/T 5332—2005)［1］(以下简记为《规程》)推荐的两种混凝土断裂韧度测定标准方法.为满足不具有尺寸效应的最小尺寸的要求，《规程》对试件的标准尺寸进行了规定，如楔入劈拉试件推荐尺寸为200 mm ×200 mm ×200 mm. 在荷载作用下，混凝土结构的承载能力大都具有较明显的尺寸效应，但其尺寸效应的大小难以定量描述，不利于正确评判结构的性能. 许多学者对混凝土断裂韧度等参数的尺寸效应问题进行了研究，试图建立尺寸与断裂参数的关系.Bazant Z P 等通过量纲分析，采用线性拟合来表述混凝土、岩石等准脆性材料的尺寸效应［2－4］. HU Xiao-zhi 等基于局部断裂能，利用双线性边界效应模型解释了尺寸效应是裂缝长度、试件尺寸和边界三者相互作用的结果［5］. 在经典的理论基础上，有学者采用试验方法对混凝土断裂参数的尺寸效应问题进一步开展了研究. 较多的试验结果证明［6－7］，断裂韧度测定在采用三点弯曲梁试验的结果中一般不具有尺寸效应，而在采用楔入劈拉法的结果中则具有尺寸效应. 因而有必要对楔入劈拉试件断裂韧度的尺寸效应问题进行进一步试验研究.

目前，楔入劈拉试件断裂韧度的计算主要采用有限元法、权函数法及其他的近似方法，并没有统一的计算公式［8－10］.《规程》给出的标准楔入劈拉试件近似采用了紧凑拉伸试件的断裂韧度计算公式，忽略了竖向力作用的影响.实际上，荷载和自重产生的竖向力与支座反力并不完全共线，尤其是非标准试件所产生的偏差更大，因而计算结果的粗略会对尺寸效应的研究产生一定影响. 要解决楔入劈拉试件断裂韧度计算不准确的问题，笔者认为主要有两种途径:①调整夹具以消除竖向力对裂缝尖端断裂韧度的影响，进而套用紧凑拉伸试件计算公式进行计算;②推导出适应于楔入劈拉试件断裂韧度计算的准确公式.基于以上思路，在对楔入劈拉试件加载装置进行调整以满足途径①的基础上，采用叠加原理推导了适应于不同尺寸楔入劈拉试件断裂计算的公式，研究尺寸变化对混凝土楔入劈拉试件双K 断裂韧度的影响规律.

1 断裂参数的计算

非标准楔入劈拉试件断裂韧度并没有统一的计算公式，可利用Tada H 等［11］推荐的单边开口受轴拉作用和纯弯矩作用计算公式叠加而得其计算式.图1为楔入劈拉试件整体受力图，外荷载加载中心和支座均位于试件四分点处，故外荷载产生的竖向力Pv和试件自身重力mg 均可由支座反力抵消，从而可简化为试件只受外荷载产生水平力Ph的作用，进一步可以等效为试件受轴拉和纯扭叠加作用，如图2所示.

图1 楔入劈拉试件受力图

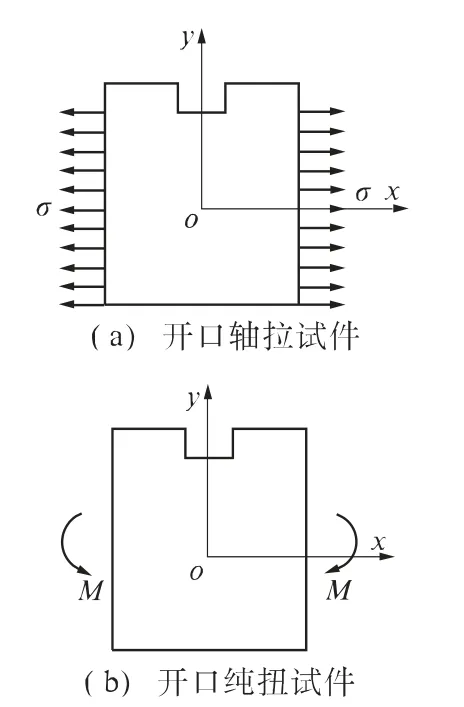
图2 楔入劈拉试件等效受力图

图2(a)开口轴拉试件荷载－裂缝张口位移关系为［11］

式中:CMODP为由轴拉力产生的裂缝张口位移;E为试件的计算弹性模量;a 为初始缝长;α 为试件的缝高比，α=a/D;σ 为由轴拉力产生的截面正应力，σ=P/(tD);t 为试件的厚度.

图2(b)开口纯扭试件荷载－裂缝张口位移关系为［11］

式中:CMODM为由纯弯矩产生的裂缝张口位移;M试件水平力对中心轴的弯矩，

根据叠加原理，裂缝张口位移为

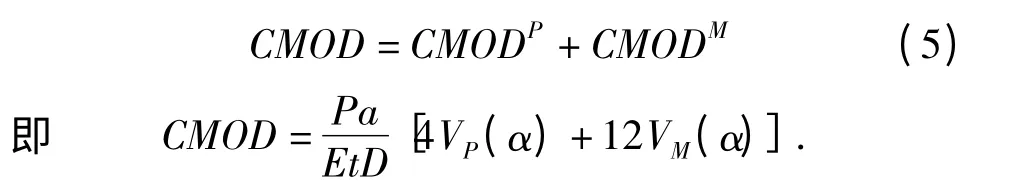
裂缝起裂前，a=a0，材料处于线弹性阶段，根据试验曲线得到的初始柔度，结合式(1)—(5)，就可以得到弹性模量的计算公式，

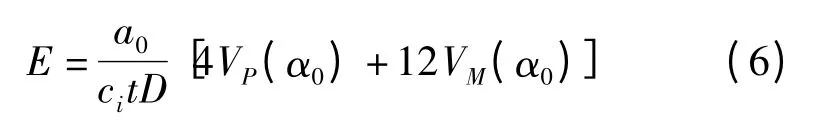
式中:α0=a0/D;ci=CMODi/Pi，通过对P-CMOD 直线上升段线性回归得到.

根据线弹性渐进叠加假定，当达到最大荷载Pmax，裂缝张口位移达到临界值CMODc且裂缝长度也发展到临界有效裂缝长度ac. 因此，把试验测得的最大荷载Pmax及对应的CMODc和由式(6)计算得到的弹性模量E 代入式(5)，再用数学软件Mathmatic 编程计算得到各个试件的临界有效裂缝长度ac.

对于图1所示的楔入劈拉试件，其受力状况可由图2等效替代，其裂缝尖端应力强度因子可由两种受力状况作用下的应力强度因子叠加而得，即

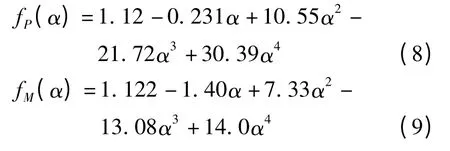
2 试验概况

2.1 试件设计

试验设计5 组共20 个不同尺寸的楔入劈拉试件，其缝高比均为0.4，截面高度分别为200，400，500，600，700 mm.试件具体参数见表1.混凝土设计强度等级为C25，采用木模浇筑，室内养护成型.

表1 试件尺寸及参数

2.2 加载及测试

试验加载及测试装置如图3所示.所有试验均在500 t 压力机上进行，严格控制加荷速率均匀连续至试件开裂破坏，最大荷载加载速率不超过10 N/s，整个过程历时约30 min.在《规程》推荐的加载装置基础上设计了一套适应于不同尺寸的楔入劈拉加载装置，将加载滑轮中心控制在试件四分点竖向平面内，以抵消荷载竖向力和试件自重的作用.所有试件均呈劈拉破坏，且断裂面大都在竖向平面内，加载装置满足要求.典型试件破坏形态如图4所示.

荷载采用0 ～50 kN 的拉压式传感器记录，裂缝张开口位移由－1 ～4 mm 的夹式引伸仪测量，裂缝尖端及韧带方向的应变采用40 mm 电阻应变片量测，最后用静动态应变采集仪对上述参数进行实时采集记录.

图3 试验加载及测试装置

图4 典型试件破坏形态

3 试验结果分析

按式(6)求得每个试件的弹性模量E，再将E，Pmax，CMODc及尺寸参数代入式(5)，通过数值计算易得ac，并通过Δac=ac－a0可得裂缝亚临界扩展量Δac，最后将起裂状态和失稳状态对应的参数代入式(7)，即可求得各个试件的起裂断裂韧度KiniIC 和失稳断裂韧度KunIC.具体计算结果见表2.

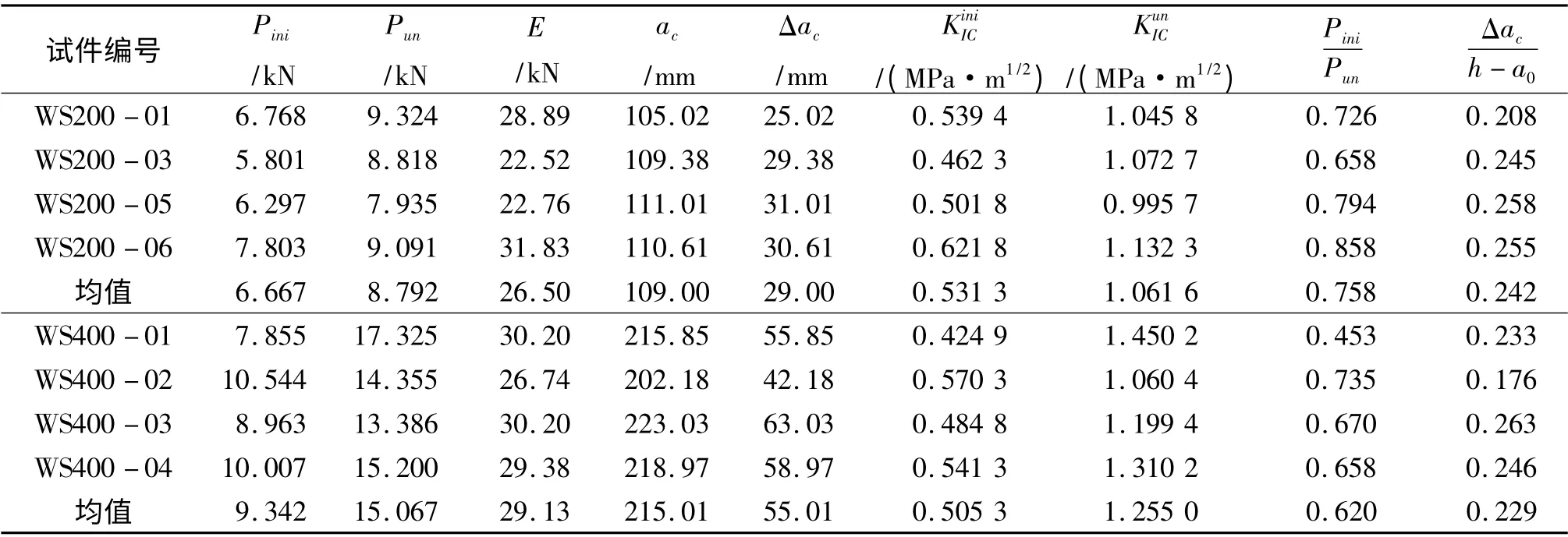
表2 混凝土断裂参数计算结果

续表

3.1 起裂荷载和失稳荷载

布置在裂缝尖端的电阻应变片用于监测起裂.混凝土试件起裂以前，裂缝尖端的拉应变随荷载增加而不断增大.当混凝土起裂时，混凝土释放能量，初始裂缝尖端拉应变开始变小. 故裂缝尖端荷载－应变关系曲线上拉应变开始回缩的转折点对应的荷载即为试件的起裂荷载Pini. 加载过程中对应的最大荷载即为试件的失稳荷载Pun.

由表2的计算结果可知，随着试件截面高度的增加，Pini与Pun均逐渐增大，起裂荷载与失稳荷载比值的平均值约为0.620，且各组相近. 这表明，虽然起裂荷载与失稳荷载均随试件截面高度的增大而增大，但两者比值趋于稳定.

3.2 临界有效裂缝长度与裂缝亚临界扩展量

裂缝亚临界扩展量为试件从起裂到失稳后裂缝的扩展长度，即Δac=ac－a0. 临界有效裂缝长度与裂缝亚临界扩展量两者能表征试件的韧性水平，临界有效裂缝或裂缝亚临界扩展越长，试件从起裂到失稳所经历的扩展距离越长，韧性越大.图5为临界有效裂缝长度ac与裂缝亚临界扩展量Δac随试件高度的变化曲线.

图5 ac 与Δac 随试件截面高度的变化曲线

由图5可知，ac随试件高度的增加而逐渐增大，且基本呈线性增长趋势.Δac随试件高度的增加而增大，但趋势变缓. Δac与韧带高度(h－a0)之比能表征试件的扩展程度，由表2可知，各试件比值的均值为0.188 ～0.242，表明随着试件高度的增大，裂缝扩展程度变化不大.

3.3 起裂韧度与失稳韧度

图6 与随试件截面高度的变化曲线

分析其原因，主要是受边界效应的影响.当截面高度较小时，试件下边界对裂缝起裂和亚临界扩展有着较大的约束作用.当试件高度低于500 mm 时，裂缝断裂过程区距离下边界较近，裂缝扩展受到限制作用较大，因而低于真实值. 当试件高度大于500 mm 时，裂缝断裂过程区扩展受下边界影响较小，甚至可以忽略，因而趋于稳定.因裂缝尖端距下边界较远而受影响较小，因而其值亦趋于稳定.

4 结 语

在完成不同尺寸楔入劈拉试件试验的基础上，利用应力强度因子的叠加原理计算不同截面高度的试件的起裂断裂韧度和失稳断裂韧度，得到以下结论.

1)起裂荷载Pini、失稳荷载Pun随试件截面高度的增大而线性增长，且两者的比值趋于稳定.

2)临界有效裂缝长度ac随试件截面高度的增大而线性增大，但裂缝扩展程度受试件高度的影响不大.

［1］河海大学，大连理工大学，中国水电顾问集团贵阳勘测设计研究院，等. DL/T 5332—2005 水工混凝土断裂试验规程［S］.北京:中国电力出版社，2006.

［2］Bazant Z P. Size effect in blunt fracture:concrete，rock，metal［J］. Journal of Engineering Mechanics，1983，110(4):519－535.

［3］Bazant Z P，Kazemi M T.Determination of fracture energy，process zone length and britleness number from size effect，with application to rock and concrete［J］. International Journal of Fracture，1990，44:111－131.

［4］Shah S P.Size-effect method for determining fracture energy and process zone size of concrete［J］. Materials and Stuctures，1990，23(6):461－465.

［5］HU Xiao-zhi，Wittmann F H. Fracture energy and fracture process zone［J］. Materials and Structures，1992，25(6):319－326.

［6］范向前，胡少伟，陆俊. 非标准混凝土三点弯曲梁双K断裂韧度试验研究［J］. 建筑结构学报，2012，33(10):152－157.

［7］张秀芳，徐世烺，高洪波.混凝土楔入劈拉试件双K 断裂参数叠加计算及其边界效应［J］. 大连理工大学学报，2006，46(6):868－874.

［8］Guinea G V，Elices M，Planas J.Stress intensity factors for wedge-splitting geometry［J］.International Journal of Fracture，1996，81:113－124.

［9］Shailendra Kumar，Barai S V. Determining double-K fracture parameters of concrete for compact tension and wedge splitting tests using weight function［J］. Engineering Fracture Mechanics，2009，76:935－948.

［10］徐世烺.混凝土断裂试验与断裂韧度测试标准［M］.北京:机械工业出版社，2010.

［11］Tada H，Paris P C，Irwin G R. The Stress Analysis of Cracks Handbook［M］.New York:ASME Press，2000.