基于脉冲宽度预测的速度反馈机制研究
张永康 张勇军 王 京 李华德
(1.北京科技大学冶金工程研究院 北京 100083 2.北京科技大学自动化学院 北京 100083)
1 引言
随着电力电子技术的飞速发展,交流电机变频调速系统得到了广泛应用,而速度传感器在高性能交流电机变频调速控制系统中具有举足轻重的作用,同时由于工业环境的特殊性也使得速度传感器成为控制系统的薄弱环节。首先,工业现场机械设备的振动和传感器安装的不规范使速度传感器出现偏心现象,从而使反馈速度在每一转的全局范围内出现低频振荡,更甚者易使传感器发生本体故障。其次,工业粉尘、气体、油污以及接线不规范也会造成速度传感器线路发生短路和断路故障。另外,各类感性[1]、容性设备[2]和其他开关型设备[3]大量应用所带来的电磁干扰,使速度传感器信号的精度受到影响。因此,如何有效提高速度传感器的可靠性和检测精度已成为调速控制系统研究中的重要内容[4]。
由于速度传感器安装位置的偏心问题易引起反馈速度在每一转的全局范围内出现低频振荡,该类问题所引起的速度误差需要经过特征提取和判断过程,属于信号辨识的范畴,无法从脉冲特征中解决,因此本文仅就速度传感器的故障和干扰问题进行研究。国内外学者为解决速度传感器故障和干扰问题所做的研究主要分为两类,一类是无速度传感器控制技术[5-8]。无速度传感器控制技术虽然具有降低编码器安装复杂性和成本等优点,但在实际应用中还存在一些难以解决的问题。首先,电压与电流信号检测过程中引入的噪声以及参数变化等使得无速度传感器技术在低速运行时的控制相当困难[9]。其次,无速度传感器技术在电机具有较高初速度情况下不具备快速启动的能力,会引起系统速降与系统振荡[10]。因此无速度传感器技术无法完全满足高性能调速系统的精度要求。另一类方法是对速度传感器信号进行滤波的方法[11-14]。现有的硬件滤波方法主要是针对脉冲信号采用RC 低通滤波器实现特定频率的干扰抑制,不具有普遍适用性。工程应用中的软件滤波方法有低通滤波器、自适应滤波器、扩展卡尔曼滤波器、FIR 滤波器等,然而此类滤波器仅作用于经计数器转换后的转速信号,无法对原始脉冲信号进行干扰辨识和抑制。
为提高速度传感器的可靠性和检测精度,本文提出采用脉冲宽度预测方法解决传感器故障和干扰问题。首先,从速度传感器的原始脉冲信号入手,通过对速度检测环节建立数学模型,推导出调速系统所能承受最大加速度情况下的速度传感器信号占空比公式。其次,通过定义占空比失真度,得出不同转动位置下的占空比变化规律,据此预测下一时刻传感器脉冲宽度范围,根据下一时刻计算所得的占空比失真度就可以辨识系统故障和干扰。为防止系统出现对传感器偶发性故障和微小干扰过度敏感所引起的振荡,选择合适的故障容忍度和干扰容忍度来辅助故障和干扰的辨识。最后,建立基于扩张状态观测器的感应电机速度观测环节,将故障、干扰辨识结果和扩张状态观测器观测的速度相结合,建立相应的速度反馈机制。在实验平台上的测试结果证明了本文所述速度反馈机制的有效性。
2 速度传感器脉冲宽度预测
2.1 速度检测环节建模
实际工业应用中,速度传感器以增量式编码器为主。增量式编码器输出信号为脉冲信号,由于任何脉冲均具有上升沿和下降沿,为保证正常使用,速度传感器均会有适用转速范围。在适用范围内,传感器送出的脉冲信号上升沿时间和下降沿时间对于整个脉冲周期来说可以忽略不计。因此,本文对传感器信号的研究均在传感器的适用转速范围内,忽略脉冲上升沿和下降沿时间的影响。系统稳态运行时该类型编码器的理想信号波形为周期不变、占空比恒为50%的标准方波。受电磁干扰后的编码器信号不但周期与占空比均发生了变化,而且信号中含有一些尖脉冲,增大了单位时间内的脉冲数,引入较大的转速测量误差。图1 所示为增量式编码器的原理图。由于信号A、B仅相位不同,其他参数均相同,因此本文仅就A相信号进行分析。
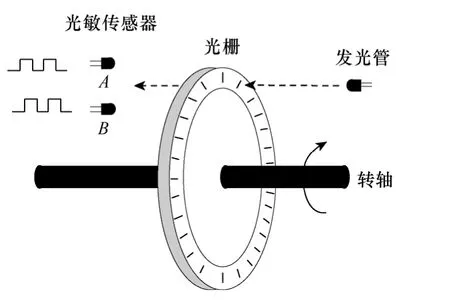
图1 增量式编码器原理图Fig.1 Schematic of incremental encoder
编码器光源扫过光栅的一个透光区和一个不透光区即送出一个周期的脉冲信号。设光源扫过光栅某个透光区域Sk所用时间为tk,扫过下一个相邻不透光区域Sk+1所用时间为tk+1,则占空比表达式为

令k∈{1…N},则从零速开始扫过前k个光栅区域的时间与扫过的角度关系为

由式(3)得

则光源扫过第k个区域所用的时间为
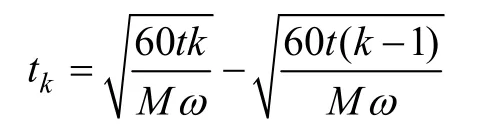
同理扫过第k和k+1 区域的总时间为

将tk和tk+tk+1代入式(1)得占空比为

由于电机以最大匀减速度进行的减速过程是匀加速过程的反过程,故可以仅就加速过程分析编码器信号。由式(4)可见,在最大匀加速过程中,编码器信号的占空比与电机加速时间t、角加速度a、编码器线数M以及电机额定转速ω无关,仅与电机加速过程中光栅转动的数量k有关,同样也可以证明在以其他加速度下进行的速度变化过程也遵循此规律。由于电机在任意稳定转速上进行的加减速均可以等效为最大加速度过程中某一阶段的加减速过程,因此式(4)具有通用性。
2.2 脉冲宽度预测
为评判占空比失真的大小,定义单个脉冲的占空比失真度为

式中,d表示单个脉冲的占空比,0.5 表示标准方波脉冲的占空比(即50%)。由于式(4)具有通用性,而式(5)是式(4)的线性变换,因此式(5)在电机的加减速过程中也具有通用性。表1 所示为无电磁干扰情况下电机匀加速过程中编码器光栅转过的区域数目k、占空比d以及占空比失真度D关系。图2 显示了表1 中各个变量的变化趋势。

图2 占空比和占空比失真度趋势图Fig.2 Trend chart of the duty cycle and duty cycle distortion

表1 电机加速过程中编码器信号关系Tab.1 The relationship between k,d and D
由表1和图2 可见,在电机最大匀加速过程中,编码器信号占空比d按式(4)进行变化。从零速开始在光源转过前25 个光栅区域的过程中,编码器信号占空比具有较大变化,此后的区域中占空比d快速趋近于0.5。相应的占空比失真度D也具有相同的趋势。由于式(4)和式(5)在电机加减速过程中具有通用性,因此在已知当前信号脉冲宽度的基础上可以利用式(4)和式(5)预测下一脉冲的宽度,即编码器信号脉冲宽度预测,以此实现对编码器故障和干扰进行在线计算和判断。
考虑到式(4)复杂的计算过程难于在普通DSP等数字处理芯片中完成,为提高故障和干扰的辨识速度和精度,节省计算资源,利用表1和图2 的分析结果,设定合适的干扰容忍度D'(0<D'<1)将实际脉冲占空比失真度限定在一定的范围内,以此实现简化式(4)和式(5)的复杂计算过程。例如,检测到当前时刻编码器内部光源扫过光栅某一区域所用时间为tk,则预测光源扫过光栅下一区域所用时间tk+1满足

式(6)分解得tk+1的范围为

若检测到编码器内部光源扫过光栅下一区域所用时间落在式(7)所示的范围内,则表示脉冲信号正常,否则可以判定为干扰脉冲。
速度传感器发生本体故障、线路短路或断路故障易引起速度反馈丢失,此时应送出故障信息并采取相应措施。但是工业现场也可能发生由不可知因素引起的速度信号脉冲偶发性丢失,且信号连续丢失的个数较少,若将此类状况归入传感器故障则会引起系统故障复位,降低了系统的鲁棒性。为防止系统对传感器偶发性故障过于敏感而引起系统复位,定义故障容忍度K。即从当前脉冲开始,预测下一脉冲的宽度tk+1,若连续Ktk+1个时间内没有返回脉冲,则认为编码器已经损坏,或者线路发生断路或者短路。一旦K确认,则判定故障的时间仅与tk+1成正比,因此故障判定时间为可测值。另外,由于当转速ω越快时,故障判定时间Ktk+1越短,更有利于系统的安全运行。
3 基于扩张状态观测器的速度观测
根据感应电机数学模型选择定子电流和转子磁链作为状态变量,在两相静止坐标系下建立的感应电机状态方程如式(8)所示[15]。


式中isα,isβ——定子电流;
usα,usβ——定子电压;
ψsα,ψsβ——定子磁链;
ωr——转子速度;
Rs——定子电阻;
Rr——转子电阻;
Ls——定子电感;
Lr——转子电感;
Lm——互感;
Lσ——漏感,
为解决观测器开环结构下不能解决直流偏置和对扰动缺乏自适应调节能力的问题,考虑将观测到的磁链作为已知量代入到上述模型中,形成闭环结构的扩张状态观测器,增强模型的确定程度,减轻观测负担。闭环磁链观测模型如式(9)所示。

其中扩张的状态如式(10)所示。

由Popov 稳定性理论从磁链观测值中可得出转速估计表达式为[16]

4 速度反馈机制设计
本文根据所提出的脉冲宽度预测方法建立了感应电机调速系统中的新型速度反馈机制,用于解决工程应用中速度传感器本体故障、线路异常或信号受到电磁干扰等问题。
转速测量方法是将编码器信号直接进行计数处理。本文采用测量多个脉冲总时间的方法,即M/T法来计算电机转速。若m1个脉冲的总时间为m2个系统采样时间,容易推导出M/T 法的速度实测值计算式为

式中,fc为系统采样频率;P为增量式编码器线数。低速时,编码器单个脉冲持续时间较长,若继续按照式(12)计算转速,将大大增加系统的等待时间,为此增加以下前提条件:设定脉冲宽度上限Tk,若编码器脉冲时间tk>Tk则ωMT=0,否则按照式(12)计算转速。
若根据式(7)判定m1个脉冲中受干扰的脉冲个数为m3,可定义速度误差率为DMT

DMT的值用于对编码器信号干扰的补偿。
速度反馈机制流程如图3 所示。

图3 速度反馈流程图Fig.3 Flowchart of speed feedback
该机制主要实现如下功能:
(1)系统上电后对故障容忍度和干扰容忍度等参数进行初始化。
(2)采集并计算当前编码器信号的脉冲宽度tk,根据设定的干扰容忍度D'和式(7)预测下一脉冲的宽度范围tk1+。
(3)采集下一脉冲的宽度tk'1+,判断该宽度是满足式(7)。若满足则按照式(12)所表示的M/T法计算电机速度,以此结果作为速度反馈参加闭环控制。否则判定该脉冲为干扰脉冲,并对式(12)所表示的电机转速进行干扰补偿。将定义的速度误差率为DMT作为补偿的量度,采用线性加权式(14)将状态观测器观测到的转速补偿到式(12)所表示的电机转速中,补偿后的转速作为速度反馈参加闭环控制。

式(14)中右侧第一项ωMT(1-DMT)表示速度传感器实测值中不含干扰部分的速度反馈,第二项表示使用扩张状态观测器得到的速度观测值补偿掉速度传感器实测值中的干扰。
(4)判断当前脉冲宽度tk1+是否大于。若,则判定速度传感器发生本体或线路故障,送出故障信号,并将状态观测器观测到的电机转速作为反馈速度参与闭环计算。若,继续使用第(3)步中干扰补偿后的转速作为速度反馈参加闭环控制。
改进后的速度反馈结构如图4 所示。其中ESO为式(9)和式(11)表示的基于扩张状态观测器的速度观测模块。M/T 算法为式(12)所表示的基于速度传感器信号的速度计算模块。速度误差率计算为式(13)所表示的速度传感器信号速度误差率。

图4 改进后的反馈通道框图Fig.4 System diagram of improved speed feedback channel
5 实验验证
为验证以上方法的有效性,本文在以TMS320-F2812 为算法运算核心、EP2C5T144 为逻辑运算核心的异步电动机变频调速实验平台上进行系统实验,实验平台结构如图5 所示。其中感应电动机(IM)型号为西门子1LA7096—4AA,电机参数见表2;编码器型号为西门子1XP8001—1/1024,每圈1 024线;示波器主要用于编码器脉冲信号的测量与存储;PC 的主要作用是调试程序和运行监控软件,实时显示和存储电机运行中的参数。

图5 实验系统构成Fig.5 Schematics of the experimental setup

表2 感应电机参数Tab.2 Parameters of the induction motor
5.1 速度检测环节模型验证
实验中系统的最大加速过程定义如下:电机转速从零开始,经1.5s 达到额定转速1 420r/min。加速过程中编码器信号A 通道的波形如图6 所示。将示波器波形数据存储为.csv 文件,使用 Microsoft Excel 软件对波形数据进行处理,得出编码器光栅转过的区域数目k、占空比d以及占空比失真度D关系见表3 所示,表中的占空比和占空比失真度与表1 相应数据仅有微小误差,该误差可归为测量误差。由对比结果可以证明式(4)所表示的速度检测环节模型的正确性。

图6 加速过程中的编码器信号Fig.6 The encoder signal in the acceleration process

表3 实际电机加速过程中编码器信号关系Tab.3 The relationship between k,d and D during the actual experiment
5.2 干扰容忍度和故障容忍度验证
根据宽度预测方法,在FPGA 中使用Verilog HDL 语言实现对干扰容忍度和故障容忍度的检测,实验结果如图7 所示。实验中,设定干扰容忍度为D'=0.1,故障容忍度K=2,即连续丢失两个以上脉冲宽度则认为编码器出现线路故障。实验中设定一个干扰指示IO 端口,当检测到干扰脉冲时IO 端口电平进行一次翻转;设定一个故障指示IO 端口,当判断编码器发生异常时输出高电平。图7a 所示为干扰容忍度的实验波形,由图可见当编码器脉冲含有干扰脉冲时,通过相应的干扰容忍度判断,可以准确地检测到干扰脉冲。图7b 所示为故障容忍度的实验波形,由图可见,由于故障容忍度设定为K=2,当连续丢失两个脉冲宽度时,不认为发生故障,而判定为偶发性故障,但此时相应的干扰容忍度将该脉冲判定为干扰脉冲。当连续丢失三个脉冲宽度时,则判断传感器发生故障,送出故障指示信号,相应的干扰指示也进行翻转。

图7 编码器干扰和故障判定波形Fig.7 The encoder signal when interference and fault
5.3 扩张状态速度观测器实验验证
为验证本文使用的扩张状态观测器的有效性,本文将无干扰情况下有速度传感器矢量控制下的实际转速与扩张状态观测器的速度观测值进行对比,对比结果如图8 所示,中间所示为匀速过程中的示波器放大图。由图可见,该观测器仅在系统启动初期具有较大观测误差,在系统加减速阶段均能很好地观测实际速度。由此证明扩张状态观测器在感应电机转速观测上的有效性。

图8 系统加减速过程的速度观测曲线Fig.8 Waveforms of peed estimation between acceleration and deceleration
5.4 新型速度反馈机制下的干扰补偿实验验证
图9 所示为速度传感器信号受较强电磁干扰时,按照式(14)进行干扰补偿前后的速度变化曲线。实验中设定转速为1 000r/min,并采用FPGA将随机干扰脉冲叠加到速度传感器脉冲信号中,以此模拟工业现场的电磁干扰情况。由图9 可见在3.6s时加入本文所述干扰补偿方法后,速度振荡有明显的降低,显著抑制了电磁干扰的影响,验证了新型速度反馈机制下干扰补偿的有效性。

图9 加入干扰补偿方法前后的速度曲线Fig.9 Speed waveforms before and after disturbance-compensation
5.5 新型速度反馈机制下的故障辨识实验验证
图10 显示了无干扰情况下速度传感器发生故障前后的速度变化情况。实验中设定转速为900r/min,在FPGA 中设定3.3s 时切断编码器的脉冲信号。由图可见,在故障瞬间实际速度仅有2%的跌落,并在0.3s 内恢复到额定值,虽然速度有波动,但是仍能保证系统正常运行,由此可验证新型速度反馈机制下故障诊断的有效性。

图10 速度传感器发生故障后的系统反应曲线Fig.10 System waveforms when speed sensor failures
6 结论
本文针对交流调速系统中速度传感器易发生故障和受干扰的问题,推导并建立了传感器数学模型,首次提出脉冲宽度预测的方法,通过预测下一时刻传感器脉冲宽度范围,可有效辨识传感器故障和信号干扰。通过引入干扰容忍度和故障容忍度的概念,提高了辨识速度,并将辨识结果、转速实测值以及基于扩张状态观测器的感应电机速度观测值进行有效的整合,建立一套新型的交流调速系统速度反馈机制。实验结果验证了传感器信号模型、脉冲宽度预测和所提出的新型速度反馈机制的有效性,并表明该反馈机制能够有效防止速度传感器故障及电磁干扰对系统造成的冲击,提高了高性能交流调速控制系统的抗干扰能力,具有较高的工程实用性。
[1]李晓明,梁军,王葵,等.开关特性饱和电抗器原理及其实验[J].电力系统保护与控制,2012,40(23):132-137.Li Xiaoming,Liang Jun,Wang Kui,et al.Principle and testing of a saturable reactor with switch characteristic[J].Power System Protection and Control,2012,40(23):132-137.
[2]吴勇海,蔡金锭.中压配电网串联电容补偿调压技术研究及应用[J].电力系统保护与控制,2012,40(13):140-143.Wu Yonghai,Cai Jinding.Study and application of voltage regulation technology by series capacitance compensation in medium voltage distribution network.[J].Power System Protection and Control,2012,40(13):140-143.
[3]吕学志,康忠健,梅永超.基于无源性理论的电压不平衡条件下 PWM 整流器非线性控制策略[J].电力系统保护与控制,2013,41(6):71-76.Lü Xuezhi,Kang Zhongjian,Mei Yongchao.Nonlinear control of PWM rectifier based on passivity theory under unbalanced grid voltage[J].Power System Protection and Control,2013,41(6):71-76.
[4]周东华,胡艳艳.动态系统的故障诊断技术[J].自动化学报,2009,35(6):748-758.Zhou Donghua,Hu Yanyan.Fault diagnosis techniquesfor dynamic systems[J].Acta Automatica Sinica,2009,35(6):748-758.
[5]张永昌,赵争鸣.基于自适应观测器的异步电机无速度传感器模糊矢量控制[J].电工技术学报,2010,25(3):40-47.Zhong Yongchang,Zhao Zhengming.Speed sensorless fuzzy vector control of induction motor using an adaptive observer[J].Transactions of China Electrotechnical Society,2010,25(3):40-47.
[6]Holtz J.Sensorless control of induction machines–with or without signal injection? [J].IEEE Transactions on Industrial Electronics,2006,53(1):7-30.
[7]王高林,杨荣峰,于泳,等.无速度传感器异步电机转子磁场定向自适应鲁棒控制[J].电工技术学报,2010,25(10):73-80.Wang Gaolin,Yang Rongfeng,Yu Yong,et al.Adaptive robust control for speed sensorless fieldoriented controlled induction motor drives[J].Transactions of China Electrotechnical Society,2010,25(10):73-80.
[8]李珍国,李彩红,阚志忠,等.基于改进型简化磁链法的开关磁阻电机无位置传感器速度控制[J].电工技术学报,2010,26(6):62-66.Li Zhenguo,Li Caihong,Kan Zhizhong,et al.Switched reluctance motor sens orless speed control based on the improved simplified flux method[J].Transactions of China Electrotechnical Society,2010,26(6):62-66.
[9]邓歆,赵金.异步电机无速度传感器控制系统中磁场跟踪控制器设计[J].电工技术学报,2010,25(5):82-87.Deng Xin,Zhao Jin.Magnetic field tracking controller in speed sensorless induction motor drive[J].Transactions of China Electrotechnical Society,2010,25(5):82-87.
[10]尚敬,刘可安,冯江华.牵引电动机无速度传感器及带速度重投控制[J].中国电机工程学报,2006,26(15):118-123.Shang Jing,Liu Kean,Feng Jianghua.Speed sensorless control and restarting at unknown speed of traction motor[J].Proceedings of the CSEE,2006,26(15):118-123.
[11]程远楚,徐德鸿,刘燕.基于瞬时无功理论的 SVC低通滤波器设计与应用[J].电工技术学报,2008,23(9):138-143.Cheng Yuanchu,Xu Dehong,Liu Yan.Design and Application of low-pass filter based on instantaneous reactive theory[J].Transactions of China Electrotechnical Society,2008,23(9):138-143.
[12]王新.自适应滤波器的新型变步长算法及其应用[J].电机与控制学报,2011,15(4):23-27.Wang Xin.Novel variable step size algorithm of adaptive filter and its application[J].Electric Machines and Control,2011,15(4):23-27.
[13]李剑飞,尹泉,万淑芸.基于扩展卡尔曼滤波器的异步电机转速辨识[J].电工技术学报,2002,17(5):40-44.Li Jianfei,Yin Quan,Wan Shuyun.Identify the rotor speed of an asynchronous motor by using the extended Kalman filter[J].Transactions on China Electrotechnical Society,2002,17(5):40-44.
[14]蒋立平,谭雪琴,王建新.一种基于 FPGA 的高效FIR 滤波器的设计与实现[J].南京理工大学学报,2007,31(1):125-128.Jiang Liping,Tan Xueqin,Wang Jianxin.Design and implementation of efficient FIR filter based on FPGA[J].Journal of Nanjing University of Science and Technology,2007,31(1):125-128.
[15]苏位峰,孙旭东,李发海.基于ESO 的异步电机无速度传感器矢量控制[J].清华大学学报,2005,45(4):565-566.Su Weifeng,Sun Xudong,Li Fahai.ESO-based sensorless vector control of induction motors[J].Journal of Tsinghua University,2005,45(4):565-566.
[16]李永东.交流电机数字控制系统[M].北京:机械工业出版社,2012.

