双向LLC 谐振型直流变压器的软启动及功率换向控制

陈启超 王建赜 纪延超

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

1 引言

随着电力电子器件的不断发展和电力电子变换技术的不断进步，具备电压变换、能量传递及电能质量调节功能的新型变压器——电力电子变压器得到了越来越多的关注[1-3]。作为电力电子变压器的一种类型或是其结构中一级的直流变压器，尤其是双向隔离型DCT，已经逐渐成为国内外学者的研究热点。DCT 可以实现两个不同直流电压等级系统的连接，广泛地应用于直流输配电系统、分布式并网发电和电动汽车等领域[4,5]。

如今，许多具备软开关能力的直流变换器拓扑被应用到DCT 的研究中，以减少开关损耗、降低电磁干扰，从而提高功率器件的开关频率，在提升功率密度的同时减小隔离变压器的体积和重量。LLC谐振变换器因其具有自然软开关特性，也被作为DCT 的拓扑结构进行了分析与设计[6,7]。

然而LLC 谐振型DCT 在实际应用时也存在一定问题:一方面，在对LLC 谐振变换器进行分析时，均假设了输出滤波电容足够大以致在二极管导通时能将变压器二次电压钳位。这使得变压器在启动时需要对大容量的输出滤波电容进行充电（假设启动时电容已经放电完全），此时产生很大的冲击电流，不仅会造成功率器件的击穿，同时还会引起谐振电容的过电压而烧毁。因此，软启动控制对LLC 谐振型DCT 的启动运行尤为必要。但是DCT 的增益特性决定了传统的降频软启动方式并不适用。文献[8,9]提出的LLC 谐振变换器软启动控制策略，也都是对降频控制的改进，不能有效改善DCT 的启动状况。另一方面，LLC 谐振变换器只能工作在单向功率传递状态。尽管文献[4,10]对双向LLC 变换器进行了分析和设计，但是没有对其功率方向变换的运行状态进行研究，并未实现真正意义的双向运行。

本文研究的双向LLC 谐振型DCT 如图1 所示。首先分析了DCT 在变频控制和移相控制下工作原理和增益特性。然后根据移相控制时变换器增益随占空比单调递增的特性，提出了一种基于移相控制的软启动控制策略。根据功率方向变换会迅速体现在输出电容电压变化上的特性，采用了一种输出电压滞环控制的功率换向控制策略，对DCT 功率的流动方向加以判断，从而转换工作模式。最后，通过一台1kW 的实验样机验证了所提控制方法的正确性和有效性。

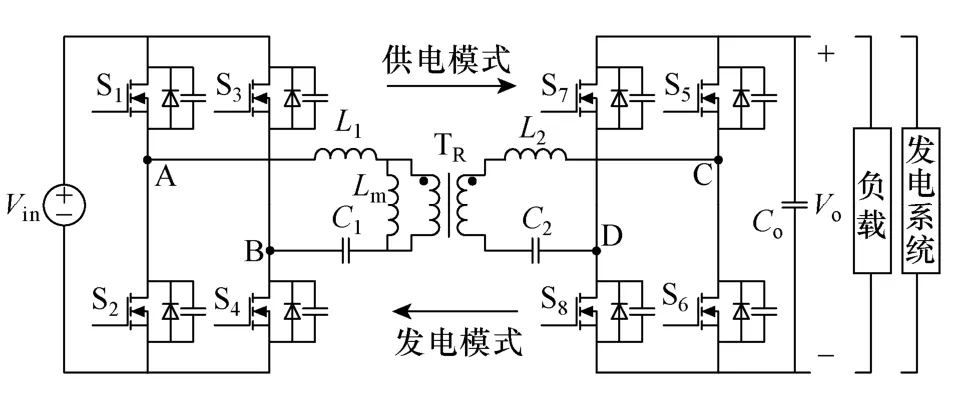
图1 双向LLC 谐振型DCT 结构Fig.1 Bidirectional LLC resonant DCT topology

2 双向LLC 谐振型直流变压器的工作原理

双向LLC 谐振型DCT 的拓扑结构如图1 所示。其中，功率器件S1～S4与S5～S8分别构成了两个全桥变换器。Lm为高频变压器TR的励磁电感，L1和L2为谐振电感，分别包含了变压器一次侧和二次侧的漏感，C1和C2为谐振电容，同时具有隔直作用。图1 中S1～S8并联的二极管和电容分别为VDS1～VDS8与CS1～CS8。变压器TR的电压比为n。为了保持双向工作特性的一致，谐振网络设计为:Lr=L1=n2L2，Cr=C1=C2/n2。

DCT 输入侧为直流母线电源，输出侧可以为负载供电，也可接纳直流并网发电系统。图1 给出了功率的流动方向，把功率由变压器一次侧传递至二次侧定义为供电模式，由二次侧传递至一次侧定义为发电模式。DCT 工作在供电模式时，S1～S4加驱动信号，实现逆变功能，而S5～S8不加驱动信号，采用开关管反并联的二极管进行整流；工作在发电模式时，对应的S5～S8加驱动信号实现逆变，S1～S4不加驱动信号实现二极管整流，此时可将励磁电感等效到变压器二次侧，则结构与正向工作时完全相同。

图1 所示的DCT 可实现双向传输功率，且无论工作在供电模式还是发电模式，都具备LLC 变换器的软开关特性，不需要额外的缓冲电路。LLC 谐振变换器的控制方式可分为变频控制和移相控制，下面以供电模式为例，对两种控制方式进行分析。

2.1 采用频率调制的变频控制

LLC 谐振变换器采用变频控制时主要的理论工作波形如图2 所示，其一个开关周期可分为8个工作阶段，前半周期和后半周期的工作原理相同。为了使工作原理的细节更清晰明了，图2 和图5 的死区时间都被放大。实际的死区时间相对于开关周期来说非常短，在下文的分析中可以忽略。

图2 变频控制时的主要工作波形Fig.2 Operation waveforms under variable frequency control

当LLC 变换器工作在谐振频率点附近时，电流波形近似正弦，可用基波分量法进行分析，从而将谐振变换器等效为一个线性网络。双向LLC 谐振变换器的基波等效电路如图3 所示。vAB1、vCD1分别为AB 和CD 两点电压的基波分量。Req为耦合到一次侧的交流等效负载，Req=8n2Ro/π2，其中，Ro为输出侧负载[11]。

图3 双向LLC 变换器的基波等效模型Fig.3 Fundamental wave equivalent model of bidirectional LLC converter

由图3 求得双向LLC 谐振变换器的传递函数为

式中，ωs为开关角频率，经过推导化简进而可以得到变换器增益M的表达式为

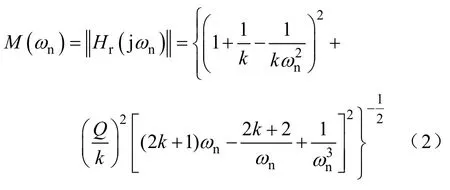
根据式（2）可以得到当k=10 时，不同Q值下的双向LLC 谐振变换器的增益曲线，如图4 所示。

图4 变频控制时的增益曲线Fig.4 Gain curves under variable frequency control

2.2 采用脉宽调制的移相控制

LLC 谐振变换器采用移相控制时主要的理论工作波形如图5 所示，其一个开关周期可分为10个工作阶段，前半周期和后半周期的工作原理相同。开关频率等于谐振频率。定义驱动信号的占空比D=2Ton/Ts，其中，Ts为开关周期，Ton为t0到t1的时间。

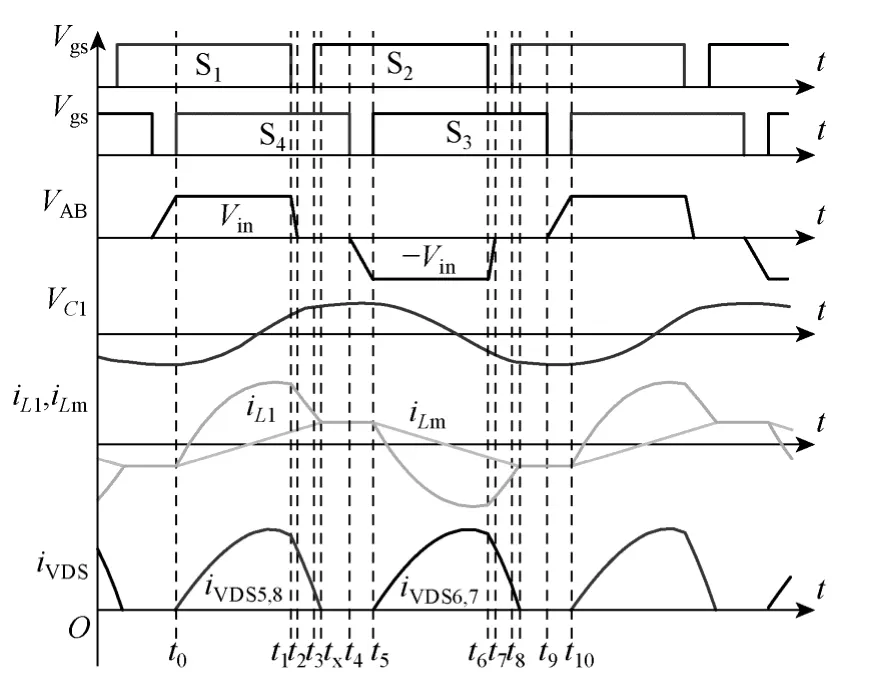
图5 定频控制时的主要工作波形图Fig.5 Operation waveforms under fixed frequency control

采用移相控制时，谐振电流的谐波分量增多，用传统的基波分析法来分析会造成较大误差，此时可采用时域分析法。文献[12]根据谐振电流iL1的变化将半个周期分为三部分，分别对应图5 中t0～t1，t1～tx，tx～t5三个时间段，然后列写了每个时间段内关于谐振电感电流iL1、谐振电感电压VC1和励磁电流iLm的暂态方程组，最后通过边界条件得到方程组

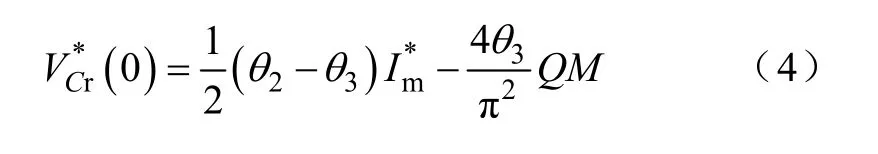
图6 定频控制时的增益曲线Fig.6 Gain curves under fixed frequency control

LLC 谐振型DCT 稳态运行时处在上述两种控制方法的交汇处，即开关频率等于谐振频率且驱动信号占空比为1。因为DCT 工作在不调压状态，这有别于输出稳压的直流变换器，后者需要根据输入电压的变化调整开关频率或是移相角，从而获得一定的增益来保持输出电压稳定。LLC 谐振型DCT工作在谐振点，此时的效率最高，增益稳定为1 且与负载无关。

3 双向LLC 谐振型DCT 的软启动控制策略

LLC 谐振变换器传统的软启动方式采用降频控制，即启动时功率器件工作在最大开关频率，逐步降至额定开关频率，利用增益曲线在最大开关频率至额定频率间递增的特性来逐渐升压，但是此方法并不适用于DCT。LLC 谐振型DCT 设计时考虑到元器件误差的影响，应尽量增大k值，使谐振点附近的增益平稳为1[6]，从而保持输出稳定。

本文根据移相控制时增益M随占空比D单调递增的特性，提出了基于移相控制的软启动控制策略。具体过程为:启动时，D和M都为0，输出电压uo为0；逐渐增加D，M也随之增加，uo上升；当D=1时，M=1，uo升压至额定电压，软启动过程完毕。

采用移相控制的软启动控制策略可有效消除启动冲击电流，同时D关于时间t的曲线也会影响软启动的效果。以图6 中Q=0.05 时的增益曲线为例，启动初期，曲线的斜率很大（空载时Q趋近于0，斜率变得更大），M随着D的增加上升非常快，此时如果D线性增加冲击电流仍然较大。将D线性上升的斜率变小会缓解电流冲击，但也延长了软启动的时间。为此对所提软启动控制策略进行改进。假设图6 中Q=0.05 的曲线函数为M=f(D)。理想的软启动状况为增益随时间线性增加，即增益关于时间的曲线为M=ht，其中h为时间系数。要获得理想的增益曲线，D关于时间的曲线应为f(D)=ht，取反函数得D=f-1(ht)。函数y=f(x)与其反函数y=f-1(x)的图像是关于y=x对称的，为此将占空比D的变化曲线设计为

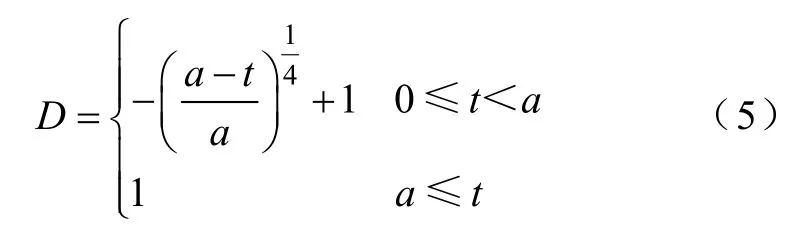
启动时M相对于D斜率较大，D上升得较平缓；随着斜率变小，D也相应地快速增加。可通过改变系数a来调整软启动过程的时间，从而使输出电压可以平稳快速的建立。

图7～图9 给出了LLC 谐振型DCT 三种启动方式的仿真波形:①无软启动情况；②软启动方式为移相角D直线上升；③软启动方式为移相角D沿式（5）曲线变化。DCT 在0.1s 时启动，两种软启动方式②和③的软启动时间为0.4s。仿真时开关信号的死区时间设定为tdead，tdead=Ts/100。尽管此时占空比D的最大值为0.98，但增益M趋近于1，死区并未对软启动过程产生影响。由图8 可知，满载启动时，采用移相控制软启动方式可使输出电压平稳快速建立，消除了冲击电流。由图9 可知，空载启动时，改进的软启动方法③可近一步降低启动电流，减小开关器件的应力。

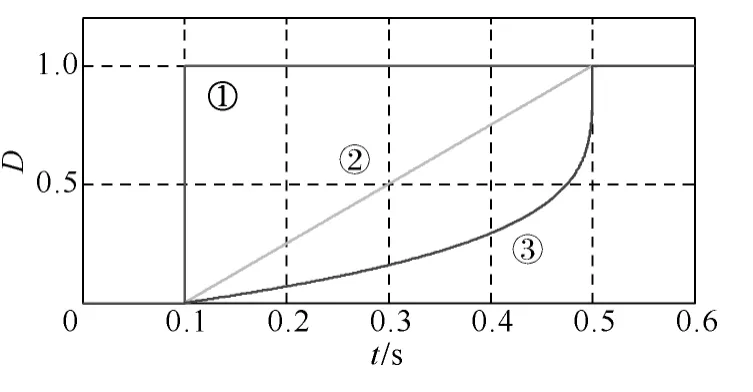
图7 三种启动方式下D 的变化曲线Fig.7 Changing curves of D under three conditions

4 双向LLC 谐振型DCT 的换向控制策略

本文所研究DCT 的输入端是直流母线，输出端可接负载或是发电系统，如图1 所示。因此可通过检测输出电容与负载或发电系统之间的电流io，来判断功率流动的方向，从而确定DCT 的工作模式。电流io为正时，DCT 工作在供电模式；电流io为负时，DCT 工作在发电模式。但是，电流检测模块应当根据满载时的电流值设计，并留有一定的裕量，因此检测较小的电流时会产生较大误差。这意味着当DCT 工作在轻载或低能量回馈时，通过检测电流来决定DCT 的工作模式可能会发生误判。

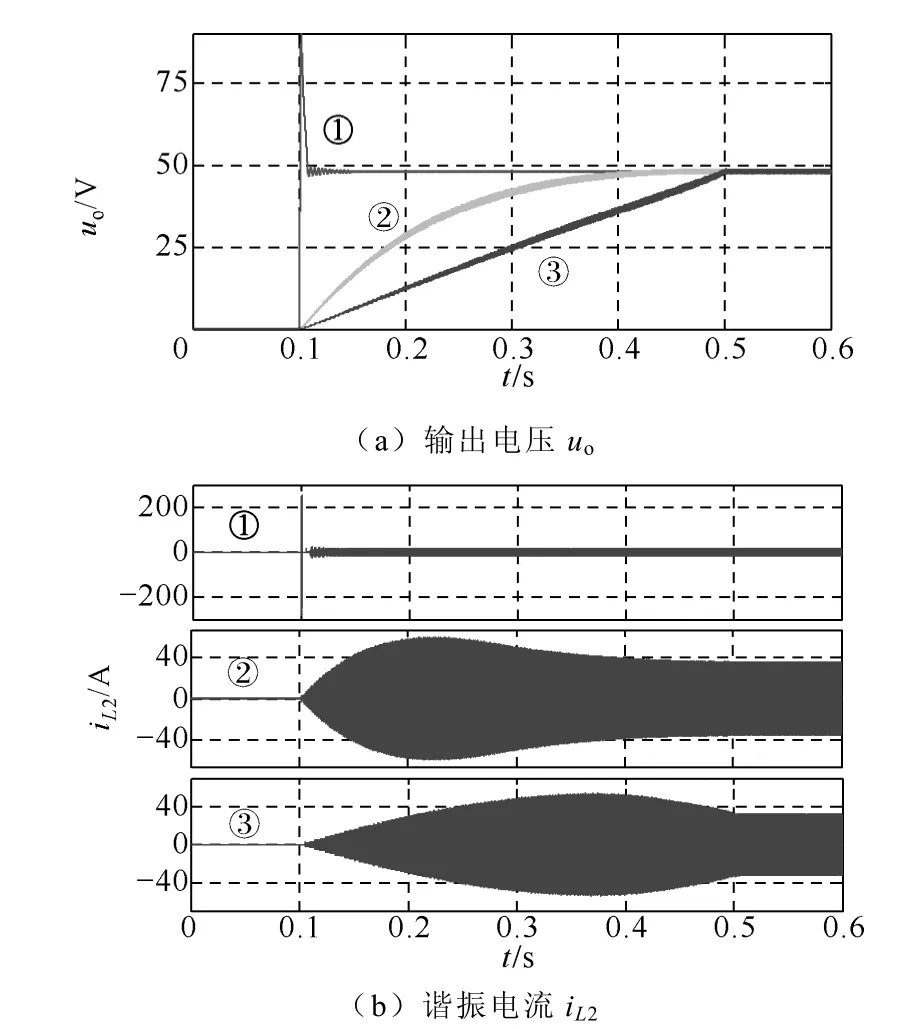
图8 满载启动时三种情况的仿真波形Fig.8 Starting simulation waveforms under three conditions at full load

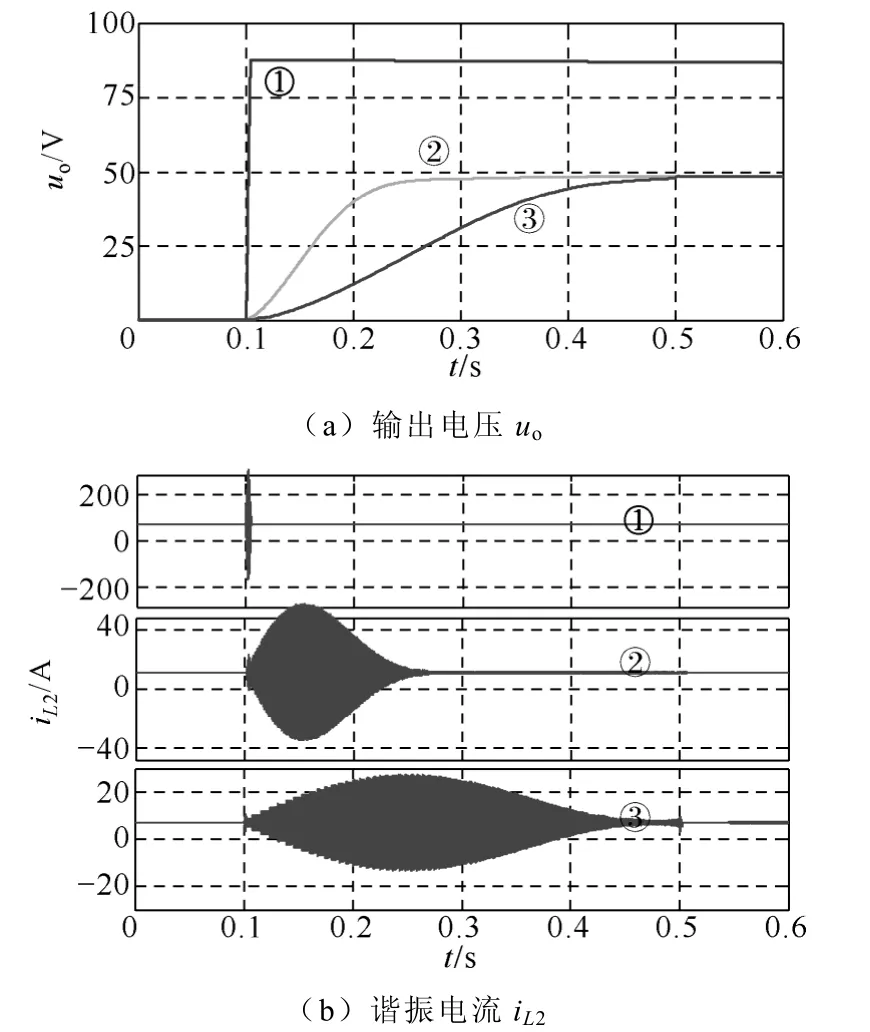
图9 空载启动时三种情况的仿真波形Fig.9 Starting simulation waveforms under three conditions at no load

本文采取一种输出电容电压滞环控制的功率换向控制策略，来调整DCT 传递功率的方向。当DCT的工作模式与实际需要的传递功率方向相反时，电容电压uo会发生变化。相反的情况有两种:①DCT工作在供电模式，而输出侧向系统回馈能量，此时电容两侧都为电容Co充电，uo快速上升。②DCT工作在发电模式，而输出侧为负载供电，此时两侧都从电容Co提取能量，uo快速下降。因此可以根据电容电压uo的变化来确定DCT 的工作模式。

假设uo变化的带宽为±r，设定模式切换的阈值为uomax=(1+r)unom，uomin=(1-r)unom。当uo＞uomax，切换为发电模式；当uo＜uomin，切换为供电模式。滞环控制的带宽r应折中选取:首先应避免由uo合理波动产生的误判，uo合理波动包括满载时±1%的纹波，负载突变引起的uo变化等；其次，应避免带宽过大导致的切换时间过长，从而引起变换器运行不稳定。综合考虑r的合理范围应为5%～8%，本文选取r为6%。

功率换向控制的仿真波形如图10 所示，图中给出了两种功率变化情况。第一种情况开始时为供电模式满载运行，0.2s 时变为轻载，0.3s 后转换为低能量回馈运行，如图10a 所示；第二种情况为供电模式与发电模式在 60%额定功率的条件下互相切换，如图10b 所示。由图可知，采用输出电容电压滞环控制的换向控制策略可以快速准确地判断出功率流动的方向，从而进行有效的模式切换。电压uo在触及阈值后，也会迅速恢复为额定电压。

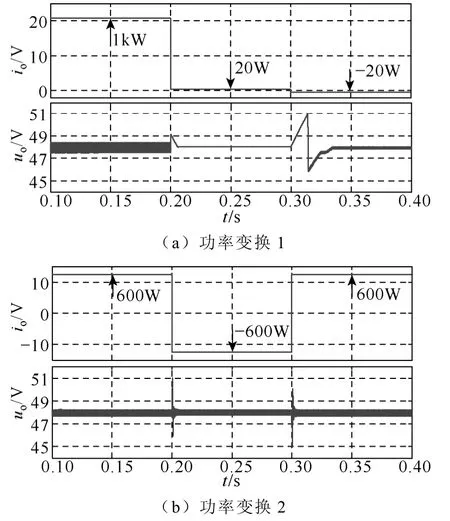
图10 功率方向转换的仿真波形Fig.10 Simulation waveforms of bidirectional power conversion

5 实验与分析

本文所提的软启动及功率换向控制策略在一台400V～48V、1kW 的双向全桥LLC 谐振型DCT 样机上得到了验证。样机选用的元件有:控制芯片，TMS320F2812（TI）；高频变压器磁心，EE42（PC40）；高压侧开关管，IPW65R310CFD；低压侧开关管，IPP070N08N3。主要的实验参数见下表。

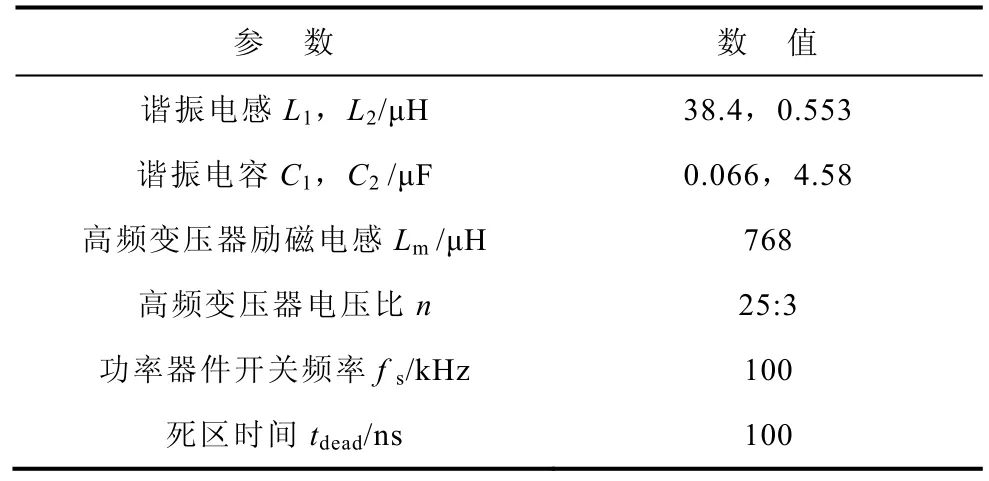
表 主要实验参数Tab. Principal experiment parameters

实验结果如图11～图15 所示，与上文的仿真结果完全一致。其中，图12、图14 分别给出了样机在满载和空载时的软启动实验波形，并与图 11和图13 所示的无软启动时的实验波形进行了对比，可见采用改进型移相控制的软启动方法可有效减小冲击电流，使输出电压快速平稳地建立起来。实验中设定的软启动时间为400ms。将图12a 中谐振电流的示意部分展开，可分别得到软启动过程和稳态运行时谐振电流iL2的波形，如图12b 和图12c 所示，与理论分析的电流波形相同。

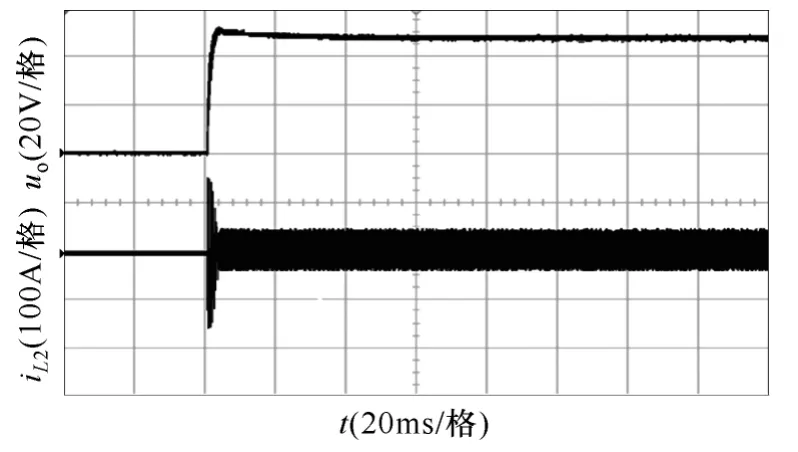
图11 满载启动的实验波形Fig.11 Starting experimental waveforms at full load

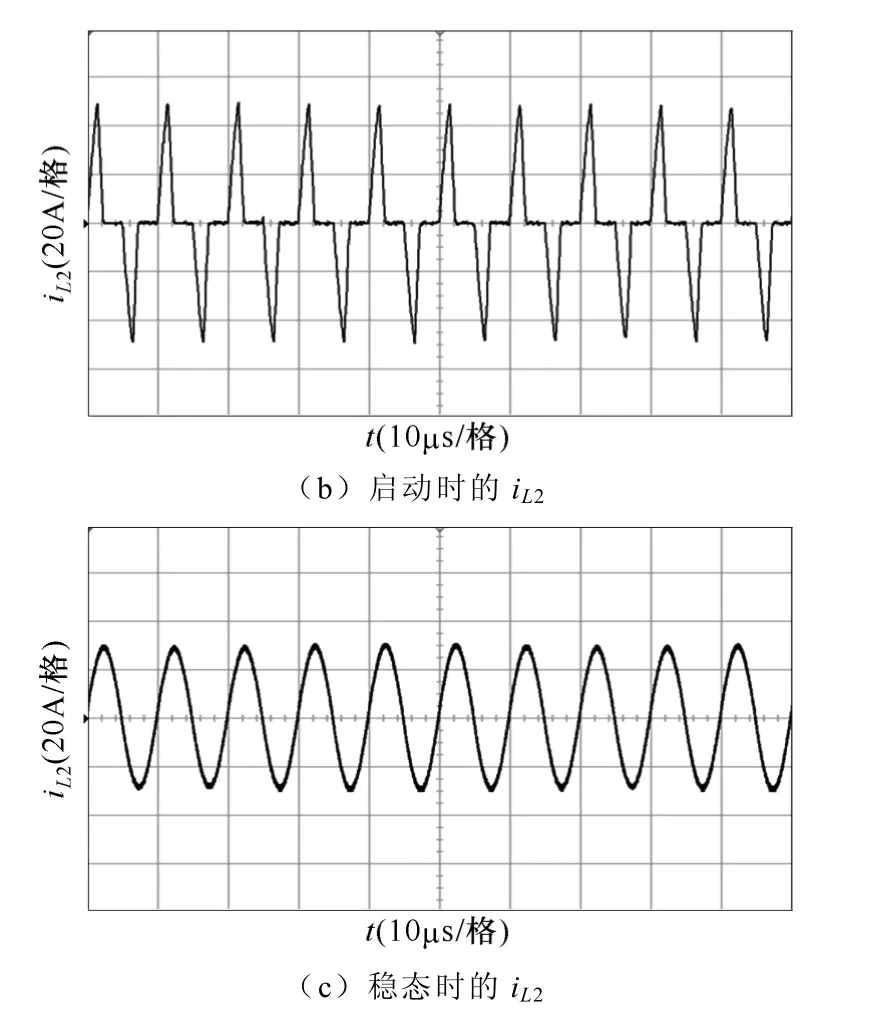
图12 满载软启动的实验波形Fig.12 Soft start experimental waveforms at full load

图13 空载启动的实验波形Fig.13 Starting experimental waveforms at no load

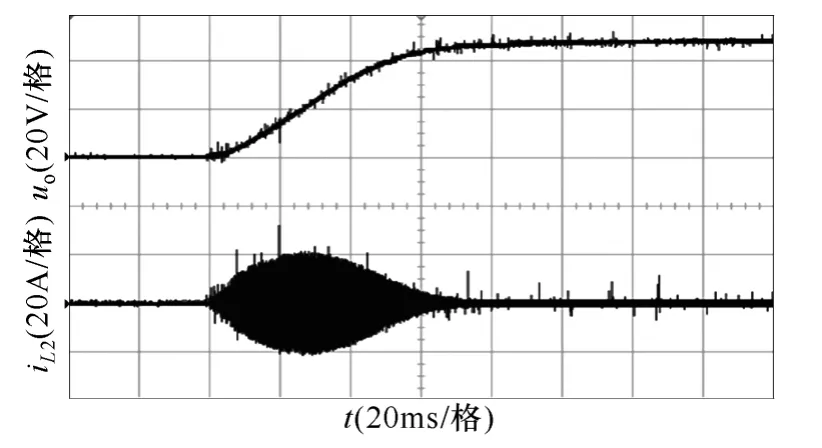
图14 空载软启动的实验波形Fig.14 Soft start experimental waveforms at no load

图15 DCT 的阶跃负荷相应Fig.15 Step load response of prototype DCT

图15 给出了样机在功率流动方向变换时，采用换向控制得到的输出电压波形。DCT 开始工作在供电模式，负载功率800W；ta时刻转换为向直流母线回馈500W 的功率，uo开始上升，因为负载较大uo上升很快，至51V 时启动换向，DCT 转换为发电模式；tb时刻DCT 又回到为功率50W 的负载供电的模式，此刻为轻载，uo下降相对缓慢，至45V 时启动换向，uo短时间内恢复为额定电压。换向控制的实验波形与仿真波形完全相符，其快速性和有效性得到了验证。

6 结论

本文对双向LLC 谐振型DCT 的控制策略进行了研究。针对LLC 谐振变换器传统的降频软启动方式不适用于DCT 的情况，提出了一种基于移相控制的软启动控制策略，有效消除了DCT 启动时的电流冲击；针对输出电流检测换向控制可能会产生误判的状况，采用了一种输出电容电压滞环控制的功率换向控制策略，可准确灵敏地判断功率方向的改变，从而转换DCT 的工作模式。通过仿真和实验，验证了所提软启动及换向控制策略的可行性和高效性。

[1]凌晨,葛宝明,毕大强.配电网中的电力电子变压器研究[J].电力系统保护与控制,2012,40(2):34-39.Ling Chen,Ge Baoming,Bi Daqiang.A power electronic transformer applied to distribution system [J].Power System Protection and Control,2012,40(2):34-39.

[2]张明锐,林承鑫,徐瑞新.一种基于固态变压器的光伏发电并网技术[J].电力系统保护与控制,2012,40(19):133-138.Zhang Mingrui,Lin Chengxin,Xu Ruixin.Gridconnected photovoltaic power generation technology based on SST[J].Power System Protection and Control,2012,40(19):133-138.

[3]刘海波,毛称雄,陆继明,等.电子电力变压器储能系统及其最优控制[J].电工技术学报,2010,25(3):54-60.Liu Haibo,Mao Chengxiong,Lu Jiming,et al.Energy storage system of electronic power transformer and its optimal control[J].Transactions of China Electrotechnical Society,2010,25(3):54-60.

[4]Chen W,Rong P,Lü Z Y.Snubberless bidirectional DC-DC converter with new CLLC resonant tank featuring minimized switching loss[J].IEEE Transactions on Industrial Electronics,2010,57(9):3075-3086.

[5]Jung J H,Kim H S,Ryu M H,et al.Design methodology of bidirectional CLLC resonant converter for high-frequency isolation of DC distribution systems[J].IEEE Transactions on Power Electronics,2013,28(4):1741-1755.

[6]陈申,吕征宇,姚玮.LLC 谐振型软开关直流变压器的研究与实现[J].电工技术学报,2012,27(10):163-169.Chen Shen,Lü Zhengyu,Yao Wei.Research and verification on LLC resonant soft switching DC-DC transformer[J].Transactions of China Electrotechnical Society,2012,27(10):163-169.

[7]Feng W Y,Mattavelli P,Lee F C.Pulse width locked loop(PWLL) for automatic resonant frequency tracking in LLC DC-DC transformer (LLC-DCX)[J].IEEE Transactions on Power Electronics,2013,28(4):1862-1869.

[8]Guo W,Bai K,Allan T,et al.A novel soft starting strategy of an LLC resonant DC/DC converter for plug-in hybrid electric vehicles[C].Proceedings of Applied Power Electronics Conference and Exposition(APEC),CA,2013:2012-2015.

[9]Feng W Y,Lee F C.Optimal trajectory control of LLC resonant converters for soft start-up[J].IEEE Transactions on Power Electronics,2014,29(3):1461-1468.

[10]Dujic D,Steinke G K,Bellini M,et al.Characterization of 6.5kV IGBTs for high-power medium-frequency soft-switched applications[J].IEEE Transactions on Power Electronics,2014,29(2):906-919.

[11]王镇道,赵亚魁,章兢,等.LLC 半桥式谐振变换器参数模型与设计[J].电工技术学报,2012,27(12):51-55.Wang Zhendao,Zhao Yakui,Zhang Jing,et al.Parameter model and design for LLC resonant halfbridge converter[J].Transactions of China Electrotechnical Society,2012,27(12):51-55.

[12]李菊,阮新波.全桥LLC 谐振变换器的混合式控制策略[J].电工技术学报,2013,28(4):72-79.Li Ju,Ruan Xinbo.Hybrid control strategy of full bridge LLC converters[J].Transactions of China Electrotechnical Society,2013,28(4):72-79.