电动汽车分散充电设施配比度分析与计算方法

陶 顺 肖湘宁 温剑锋 陈 征 章家义

（华北电力大学新能源电力系统国家重点实验室 北京 102206）

1 引言

随着能源危机和环境污染问题日益严重，电动汽车迎来了自身发展的重大契机[1-3]。充电基础设施的建设是电动汽车产业推广的前提和基石，如何合理地配置充电设施以适应电动汽车的推广应用将是急需解决的关键问题。现阶段对于充电基础设施规划配置的研究主要围绕集中式充（换）电站的站址选择与容量确定进行[4-8]，对于分散充电设施，由于其依各功能区的停车场而建，在选址方面较为简单经济，因此更应合理确定各类分散充电设施之间以及充电设施与电动汽车之间的配比度，而目前这方面的研究较少。

分散充电设施根据充电方式的不同可分为交流充电桩和直流充电设施。交流充电桩输出为交流电，需通过车载充电机为电动汽车充电，充电电流较小，充电时间一般在3～8h；直流充电设施则直接为电动汽车动力电池提供直流电源，充电电流大，一般可在半小时将电池电量充至80%以上。因此，本文分析中，慢充代表交流充电，快充代表直流充电，两类充电方式所需接口不同。美国SAEJ1772[9]以及中国2011 年颁布的GB/T 20234[10-12]一系列标准都对两类接口做了规定，目前新生产的电动乘用车基本都同时配有标准化的直流快充和交流慢充两个充电接口。充电电流过大将缩短电池寿命、降低电池效率[13-15]，且会对电网造成冲击。基于以上因素，并考虑进行有序充电的充裕度，应把慢充充电作为当前技术水平下动力电池的主要充电手段，而将快充充电作为一种辅助的应急手段。

现阶段在分散充电设施实际规划建设过程中，其配比度仍然依靠主观确定，无科学的分析方法。本文从满足电动汽车用户不同充电需求的目标出发，基于对私家车运行规律的统计分析，提出了电动汽车与慢充桩配比度和快、慢充电设施配比度的概率分析方法，为合理确定分散充电设施的配置比例提供依据。除私家车外的其余类型电动汽车（如出租车，公交车）一般都有固定的集中式充电场所，且私家车的比重将达到70%～80%，是未来电动汽车推广的主体，面向私家车的充电设施配置是否完善，将直接影响到电动汽车的发展速度，因此，本文针对电动私家车进行充电设施配比度分析，且假设未来电动汽车行驶规律与燃油车相似。

2 慢充桩与电动汽车配比度计算方法

分散慢充桩应成为满足电动汽车日常充电需求的主要设施类型，而充电需求则由多方面因素决定，包括用户的用车行为习惯、电动汽车的续航能力以及用户对电动汽车行驶性能的信心等因素，后两者决定了在分析用户充电行为时，需考虑用户心理因素。

私家车夜间一般停泊在居住区停车场，停靠时间较长。从充电的便利程度和可支配充电的时间充裕性来看，居住地是最主要的电动汽车能量补集地点，应最大程度地满足用户的充电需求，从而首先适合在居民区电动汽车用户的停车位建设分散充电桩，其数量应与该小区电动汽车数量相等，车、桩、位之比适宜为1∶1∶1，以保证为每辆电动汽车提供专有的充电服务。但是只在住宅区配置充电设施不足以完全保证用户外出行驶需求，也不利于增强用户对电动汽车的使用信心，因此，有必要在私家车用户频繁停车的其他场所配置相应的充电设施，其配比度如何确定，是本文所要分析的问题。

2.1 电动汽车用户心理接受能力分析

据文献[16]发布的2012 年上海电动汽车示范运行一周年的《数据采集报告》，大约90%的电动汽车用户会在出行前将电池荷电状态（State of Charge,SOC）充至60%以上，且大部分用户（77%）在电池剩余SOC下降到一半之前就开始充电，几乎没有人会在电量耗尽时再去充电。统计结果体现了用户对电池剩余SOC不足以维持电动汽车完成一次行驶的心理担忧。

充电桩建设数量越多，越容易满足用户的充电需求，但也意味着造成设施闲置以及投资浪费的可能性越大，因为每个用户对剩余SOC程度的承受心理不尽相同，这将直接影响其充电意愿，并非所有用户均会在停车地点充电，因此，在配置充电设施时，必须计及用户对不同剩余SOC的接受心理，从而综合考虑对充电的心理迫切性和发生充电行为的便利性，确定一个相对合理的充电桩建设比例。

2.2 桩车配比度计算方法

单个用户的充电行为具有较大的随机性，但是当样本数量足够大时，总体用户的充电行为会呈现出一定的规律，即随着样本数量的增加，对电动汽车具有相近使用心理的用户中，产生充电需求的频率将会逐渐稳定在一个值附近，即单个用户的充电概率。

本文计及不同用户对剩余SOC的接受心理，分析不同接受水平下的充电需求概率，并为其设置权重，进而综合考虑不同用户的充电需求，按适当的配比度配置交流慢充桩。

本文在分析时做如下假设:

（1）所有电动汽车均以满电状态从家出发。

（2）用户会优先考虑住宅区充电。仅当在返回住宅区之前，电动汽车能量状态可能不满足用户心理可接受水平时才在住宅区以外的场所进行充电。

（3）除居住地以外，每个用户只有一个外出目的地，且往返里程相同。

（4）行驶里程与电量消耗呈线性关系，且不考虑电池自放电。

（5）由于慢充充电时间较长，一般为3～8h，因此，假设在不同功能区的一个停车周期内（功能区车辆的平均停车时长），单个充电桩仅为一辆有充电需求的车辆服务，即不出现排队情况。

（6）对剩余SOC具有相同接受心理的用户具有相同的充电需求概率。

用户行驶及充电过程可描述如下:

根据假设（1）和（2），用户满电状态从家出发，当其到达户外目的地，可选择充电与否。这由用户对电动汽车剩余电量能否支撑其返回居住地的信心决定。后者又受以下两方面因素影响:

（1）住宅区与目的地之间的往返行程所消耗的总电量，表示为SOC的形式为SOCt。

（2）用户到家之前可接受的最低剩余SOC（用x表示）。

如果1-SOCt≤x，则用户在除家以外的目的地有充电需求，否则，回家充电。

根据假设条件（3），若用户不在除家以外的区域充电，则用户返回住宅区时的剩余SOC可表示为

式中，E为行驶所耗电量；S为电池额定容量；dt为回到住宅区前的总行驶里程；D为电动汽车续驶里程水平；dh-d为用户在家与目的地之间单次行驶里程，根据假设条件（2），dh-d为dt的1/2。

2.2.1 充电需求概率函数

不同用户对电动汽车的使用心理不同，可接受的最低剩余SOC不同，直接影响其充电意愿，因此，用户在住宅区以外地点的充电需求概率可以表示为用户心理可接受最低剩余SOC（用x表示）的函数

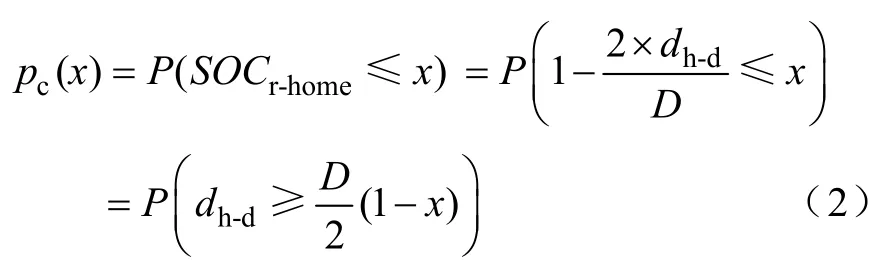
式（2）说明对用户接受心理x下的充电需求概率计算可以转化为计算单次行驶里程的概率。后文算例通过对大量数据的分析，统计满足条件的事件发生的频率来逼近相应可接受最小剩余SOC（即x）及续驶里程水平D下的充电需求概率。

2.2.2 可接受剩余SOC的权重

在不同功能区的一个停车周期内，式（2）的充电需求概率表现该时间段内所停靠的电动汽车有充电桩需求的比例，藉此可按充电需求概率去配置相应比例的充电设施。但是，从前文可以看出，充电需求概率为用户可接受SOC的函数，不同用户可接受SOC不同，在配置过程中仅考虑某一类用户的需求显然是不合适的，必须对不同用户的充电需求进行综合考虑，因此，需引入一个较为合理的权重，来反映按不同接受心理所配置的充电桩对用户需求的满足程度，从而确定一个较为合理的桩车配比度。

值得注意的是，若按用户最低心理可接受剩余SOC为x时的充电需求进行桩车比配置，则可接受最低SOC小于x的用户的充电需求也会被同时满足。从此角度考虑，引进可接受SOC的累积概率分布函数（Cumulative Distribution Function,CDF），并通过归一化来构建权重，如式（3）所示。

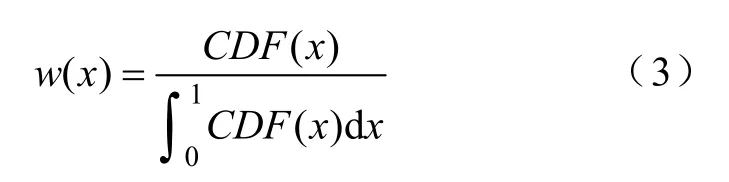
式中，x∈[0,1]为用户可接受最低剩余SOC，CDF(x)为累积分布函数，且

由于CDF(x)是一个单调不减函数，因此，w(x)也为单调不减，也就是说，从满足需求的角度来讲，按照越高的可接受剩余SOC下的充电需求概率进行充电桩配置，能满足越多用户的充电需求。值得注意的是，一部分累积概率分布并无具体的解析表达式，此种情况下，可按一定间隔分别计算各离散点xi处的权重值w(xi)，即

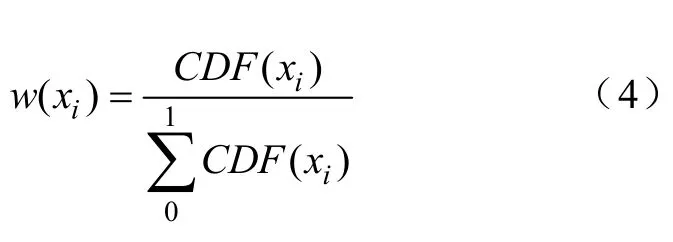
随后对各离散点w(xi)用适当的函数形式进行拟合得到w(x)的具体解析表达式。

2.2.3 车桩比计算

由上两步分别可以得到用户可接受剩余SOC为x时的充电需求概率pc(x)以及对应的权重w(x)，以w(x)为权重，对pc(x)在SOC定义域[0,1]上进行积分，可得到所有心理接受能力下用户的电动汽车与慢充桩配比度结果Rp/v

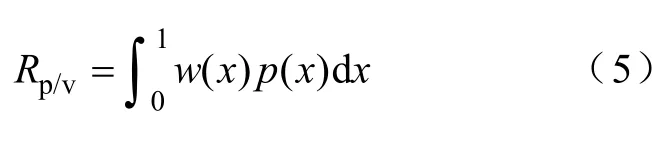
2.3 算例分析

根据以上分析可知，计算桩车比需要以下数据:

（1）为得到w(x)需要用户心理可接受最低剩余SOC 的统计数据。

（2）为得到pc(x)需要住宅区与其以外的目的地之间的单程行驶里程数据。

下文结合以上两类数据，分析续驶里程为150km（现阶段主流配置）的电动汽车所需的充电桩与车辆的配置比例。

2.3.1 充电需求概率pc(x)计算

本文使用美国家庭出行调查NHTS2009（National Household Travel Survey 2009）中的单次行驶里程数据计算城市中不同区域（工作区、商业区、休闲娱乐区）的充电需求概率pc(x)，由于统计数据是离散数据，因此，对于pc(x)的计算，本文首先针对一定间隔的xi分别按式（2）计算pc(xi)，即统计满足条件的事件发生的频率来逼近概率，之后对计算结果进行拟合得到连续函数pc(x)。根据计算结果的分布形式，本文选择式（6）所示的指数函数形式进行拟合:

图1 及式（7）～式（9）所示为各区域pc(x)计算结果。

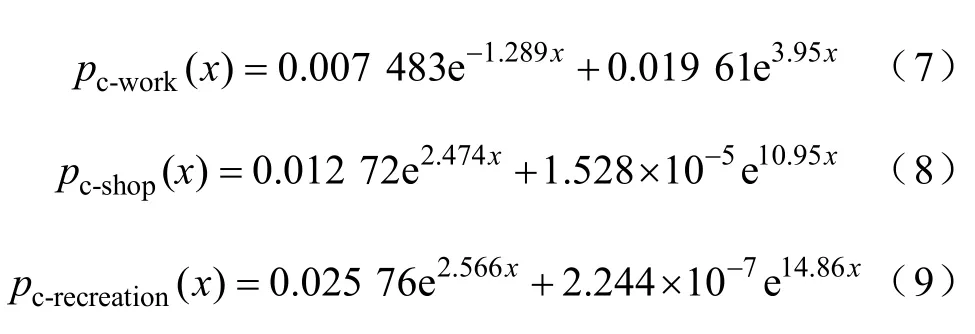
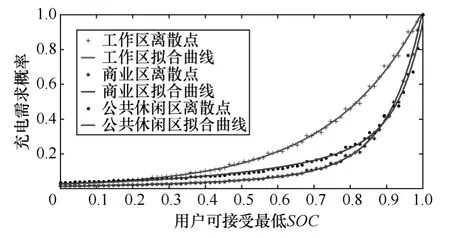
图1 各区域pc(x)曲线Fig.1 Curves of pc(x)of in different areas

从图1 可看出，用户可接受最低SOC在[0.5,1]时，工作区充电需求概率明显高于其他区域，三个区域pc(x) 拟合方均根误差（Root-Mean-Square Error，RMSE）最大为0.013，说明拟合结果相对精确。

2.3.2 权重函数w(x)计算

由于用户可接受的最低剩余SOC是一个较为主观的概念，在现阶段电动汽车尚未大量普及之前，大部分用户对此并无直观概念，难以直接获得，因此，本文使用充电起始SOC统计数据代替可接受最低SOC数据，因为充电起始SOC在很大程度上反映了用户充电心理以及其他一些与充电行为习惯相关的不可测量因素，或者可以说，充电起始SOC数据可以更好反应用户实际充电心理和行为的。

文献[17]对美国能源部发起的EV Project 项目中纯电动汽车的行驶和充电规律做了统计，其中充电起始SOC的统计结果如图2 所示，其近似服从正态分布。

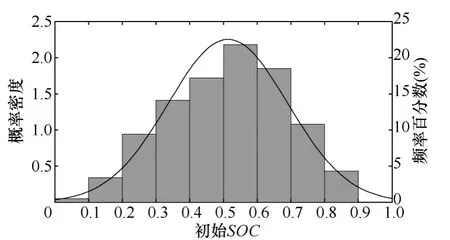
图2 充电初始SOC 频率直方图及概率密度Fig.2 Frequency chart and probability density of initial SOC

根据拟合结果可得充电起始SOC的概率密度函数:

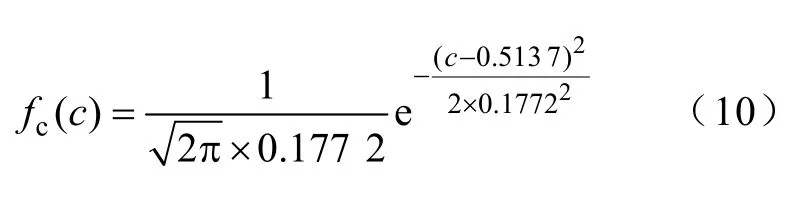
由于正态分布的累计分布函数没有解析表达形式，因此，本文使用式（4）对w(x)进行离散计算后，根据其分布形式，用5 次多项式对离散点进行拟合，拟合结果如图3 及式（11）所示。

图3 w(x)曲线Fig.3 Curve of w(x)

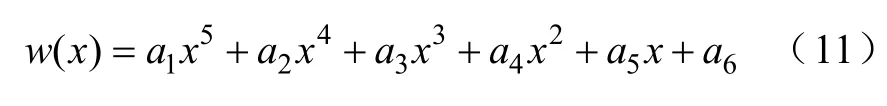
式中，a1～a6为拟合参数，见表1。

表1 拟合参数信息Tab.1 Information of the parameters

拟合的方均根误差为0.009 39，表明拟合结果较为精确。

2.3.3 慢充桩与电动汽车配比度计算结果

得到pc(x)和w(x)后，可通过式（5）确定住宅区以外的其他区域的桩车配比度Rp/v。表2 所示为各区域桩车配比度计算结果。

表2 各区域桩车比配置结果Tab.2 Configuration ratio of charging piles and EVs

前述分析以150km 续驶里程为例，表2 中同时给出了100km 续驶里程下配比度的计算结果。由式（2）可知，随着电动汽车续驶里程的不断增加，充电需求概率进而住宅区以外区域的配置桩车比会发生变化，在假设充电初始SOC不会随着电动汽车续驶里程水平改变而改变的前提下，图4 给出了桩车比随电动汽车续驶里程的变化趋势。

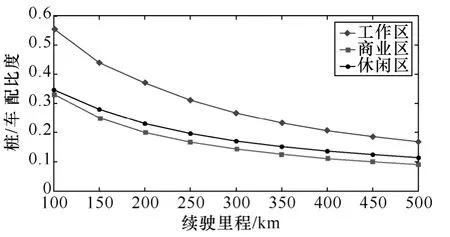
图4 Rp/v随续驶里程变化趋势Fig.4 Variation tendency of Rp/vwith driving range

可以看出，随着电动汽车续驶里程水平的提高，桩车配比度会逐步下降，且有趋近于饱和的趋势，当续驶里程达到目前燃油汽车的水平500km 时，住宅区以外各区域的桩车配比度之和只有0.4 左右，这也意味着随着续驶里程的提高，住宅区充电所扮演的角色越来越重要。实际上，随着续驶里程的增加用户对电动汽车的使用信心将会越来越大，会接受更小的剩余SOC，使得本文中权重函数也相应发生变化，从而使得桩车配比度下降较图4 更为迅速。

值得注意的是，桩车配比度的下降不等同于充电桩绝对建设数量的下降，随着电动汽车保有量的增加，仍需继续新建充电设施，但是新建慢充桩与新增电动汽车之间的比例将会同比逐渐下降。

3 快、慢充设施配比度计算方法

快速充电设施的定位是为有紧急需求的用户提供短时间、大电流的电能补给，是慢速充电桩的有益补充。规划分散充电设施时，应根据快、慢充电设施的不同定位，合理进行比例配置，以满足用户不同的充电需求。

3.1 快、慢充电设施配比度数学模型

本文以慢充的方式充电后电动汽车的能量状态能否满足用户下一次行驶的能量需求作为判断是否需要快充的条件，通过计算用户有快充需求的概率，来确定快、慢充电设施的配比度。

用户采用慢充方式充电结束时电动汽车的能量状态主要由以下两部分构成:

（1）充电开始时刻能量状态:由充电起始SOC和电池额定容量决定。

（2）慢充充电过程中所能补充的能量:由慢充充电功率与用户停车时间（反映了可用来进行充电的时间）决定。

用户为完成下一次行驶所需能量则主要由以下两部分构成:

（1）行驶所耗电量:由用户单次行驶的里程数和车辆能耗性能决定。

（2）电池允许最小剩余电量:主要由用户对最小剩余电量的接受心理以及电池安全、寿命影响等因素决定。

以上各因素中，充电起始SOC、用户停车时间及行驶里程均与用户行为习惯相关，具有一定的随机性，而电池容量、慢充功率和车辆耗电性能则主要由电动汽车具体参数决定。

因此，慢充方式不满足用户行驶需求，即用户有快充需求的条件可表示为

式中，以大写字母表示各随机变量，以小写字母表示各常量:T为停车持续时间（min）；C为初始SOC；L为单次行驶里程（km）；p为慢充方式的充电功率（kW）；s为电池的容量（kW·h）；d为电动汽车行驶每公里耗电度数（kW·h）；k为考虑用户心理以及电池安全因素所设置的电池允许最小剩余SOC。

计算（12）所发生的概率Pf，即为快充需求概率。

假设T、C、L三个随机变量相互独立，则根据三维随机变量的概率公式，可将式（13）转化为

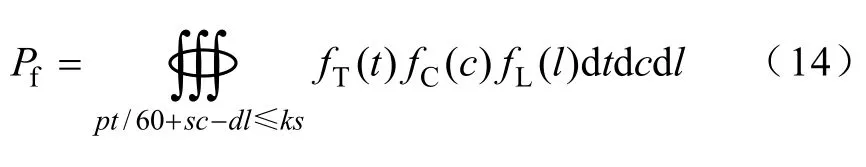
式中，fT(t)为停车持续时间概率密度函数；fC(c) 为充电起始SOC概率密度函数；fL(l) 为单次行驶里程概率密度函数。

因此，根据快、慢充需求的大小，可确定区域内所配快充和慢充设施的配比度Rf/s:

城市中不同功能区域内车辆的行驶和泊车规律不尽相同，下文以商业区为例，对快、慢速充电设施的配比度进行实例计算分析。

3.2 用户行驶及充电规律分析

准确描述电动汽车的行驶及充电规律是合理配置快、慢速充电设施的前提，由式（14）可知，计算快、慢充设施配比度需要先得到单次行驶里程、充电起始SOC以及停车持续时间三个随机变量的概率密度函数，其中充电起始SOC前文已进行分析，下文将分别对剩余两者进行分析。

3.2.1 停车持续时间

本文对NHTS 中商业区的停车时间数据进行统计，其近似服从对数正态分布，如图5 所示。

图5 商业区停车持续时间频率直方图及概率密度Fig.5 Frequency chart and probability density of parking time in shopping center

根据拟合结果可得商业中心停车持续时间概率密度函数为

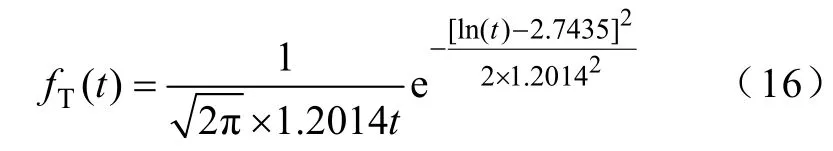
3.2.2 单次行驶里程

此处仅对NHTS 中起点或终点为商业中心的单次行驶里程数据进行统计分析。使用对数正态分布对数据进行拟合，得到图6 所示的概率密度曲线。

图6 单次行驶里程频率直方图及概率密度Fig.6 Frequency chart and probability density of trip distance

由拟合结果可得单次行驶里程概率密度函数

3.3 现有电动车型快、慢充设施配比度计算

确定式（14）中三个随机变量的概率密度函数后，本文参照现有部分电动乘用车参数（见表6）进行快慢充设施配比度的计算，对于参数k，考虑电池寿命及安全，认为动力电池最大放电深度（DOD）不宜超过80%，即最小剩余电量不应低于电池配置容量的20%，同时考虑用户的使用心理（用户不会在电量耗尽后才去充电），可设k为0.2，由于式（14）中部分被积函数的原函数没有解析表达式，因此本文通过Matlab 中的三重数值积分函数triplequa 对式（14）进行数值计算。商业区各车型参数及快慢充设施配比度计算结果见表3。

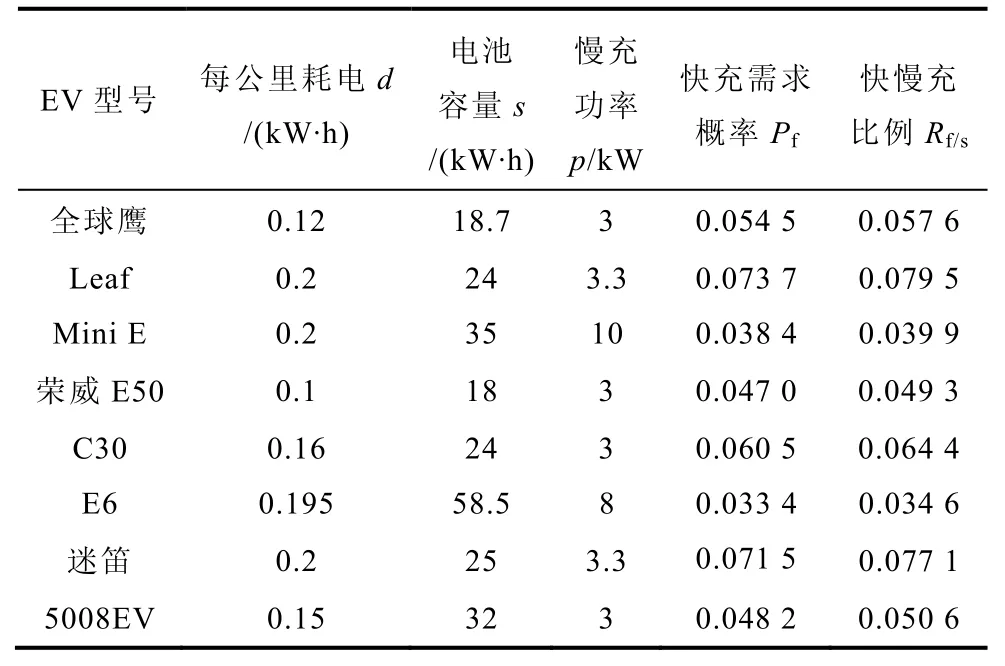
表3 各车型参数及快慢充配比计算结果Tab.3 Vehicle parameters and ratio of fast charger and slow charger

结果显示，在快、慢充配比度方面，所选车型中最大比例为0.079 5，最小为0.034 6，可知，在商业中心，快充桩可按慢充桩的4%～8%进行配置。

从分析结果可以看出，不同参数的电动汽车对快速充电的需求不同，电池容量越小、充电功率越小、而百公里耗电越大的车辆，其快充需求越大。因此，在具体配置过程中，应考虑在目标区域内进行充电的电动汽车具体参数进行配置。

4 模拟验证

针对算例所得配比度结果，本文采用NHTS 中相关行驶数据，模拟各区域用户充电行为进行验证。

为了衡量配比度是否满足实际充电需求，可定义如下参量:

（1）日需求满足率Rm:一日内可满足即到即充需求车辆数nm与总的有充电需求车辆数nd的比值，反映了所建充电桩对一日内充电需求总量的满足程度，表示为

（2）峰值需求适应度Rp:一日内有充电需求车量数的峰值nmax与充电桩配置数量Nz的比值，反映了充电桩对日最大需求的适应能力，表示为

模拟验证首先依据配比度计算充电桩配置数量。配置车桩比的基数为各区域车辆平均停车时长T内的平均停车数量NT，即

式中，n为一日内在该区域停车的总量，设各区域均为10 000 辆。根据NHTS 中各区域内乘用车的平均停车时间统计结果见表4，对式（20）中平均停车时长做如下合理假设:工作区为300min，商业区为30min，休闲区为100min。

表4 NHTS 平均停车时间统计Tab.4 Average parking duration in NHTS

根据计算得到的NT以及表2 中配比度计算结果（以150km 续驶里程下的结果为例），可确定各区域慢充桩建设数量见表5 第2 列所示。

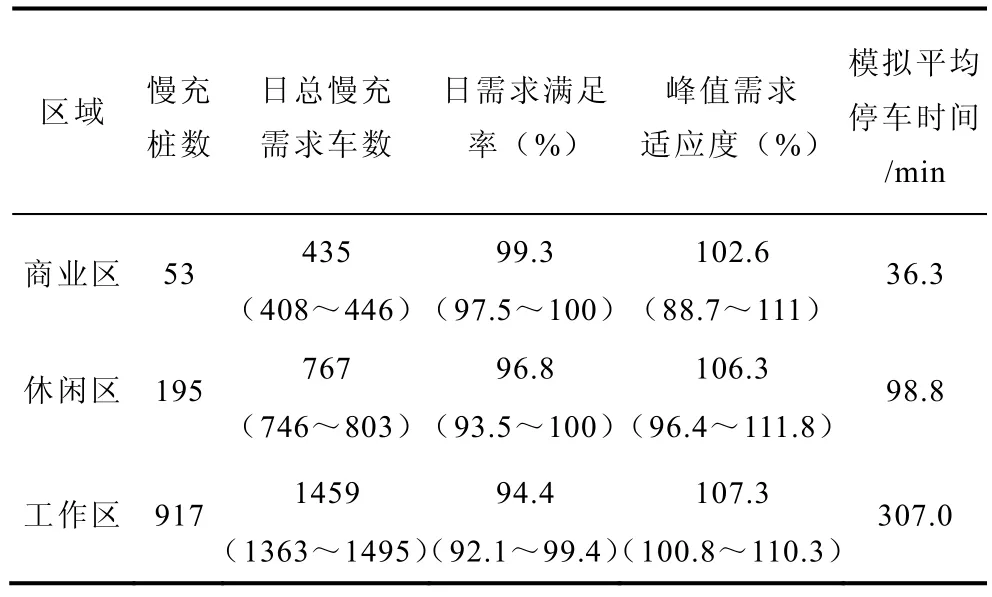
表5 慢充需求验证结果Tab.5 Results of verification for slow charging

随后模拟各区域充电行为:根据目的地区域对NHTS 数据进行分类，每次模拟从每类数据（包含到达时刻、停车时间、行驶里程）中各随机抽取10 000 组，结合前述配比度计算时的行驶规律假设条件及快、慢充判断条件，得到每个区域各时刻有充电需求的车辆数（包括该时刻正在充电车辆与新到达有充电需求的车辆）。

本文以表3 中车型C30（续驶里程150km）为例进行分析，快充功率取30kW，连续模拟10 天，结果如图7 和图8 及表5 和表6 所示。各图反映了充电需求量（有充电需求车辆数）与充电桩数量的比值随时间的变化关系，比例小于1（虚线下方区域）表示所建充电桩可完全满足该时刻用户即到即充，大于1 表示该时刻充电需求用户数量大于充电桩数量，其中灰色实细线代表每个模拟日的变化情况，黑色线为10 日内的最大、最小值包络线，灰色粗线为10 日内的平均值；各表中每栏括号外为对应指标的10 日平均值，括号内为最小值与最大值。由于本文快慢充配比度仅给出商业区算例，因此，仅验证商业区快充需求的满足程度。

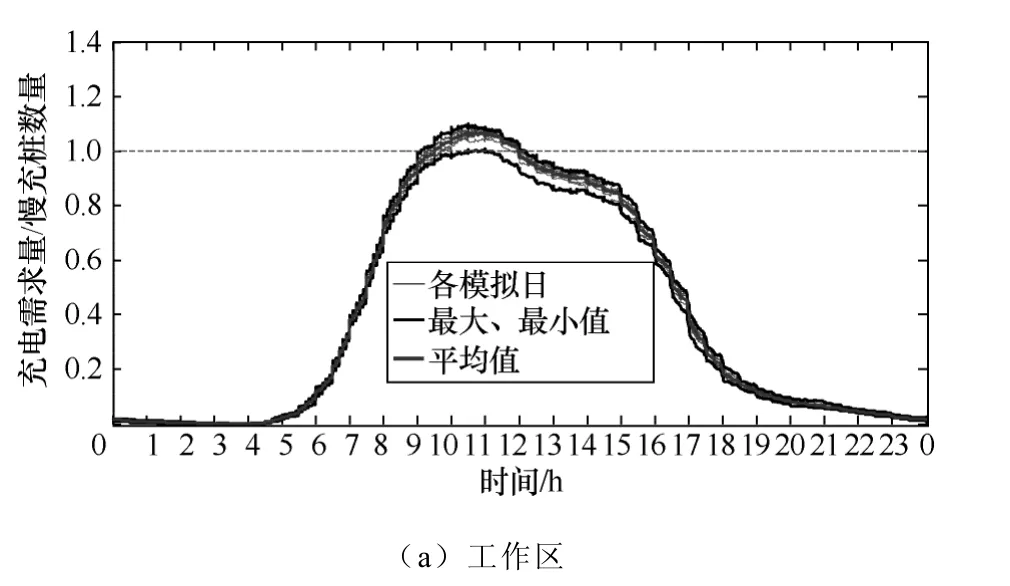
图7 各区域慢充需求与充电桩数量比值曲线Fig.7 Curves of ratio of charging demand and quantity of slow charging piles in different areas

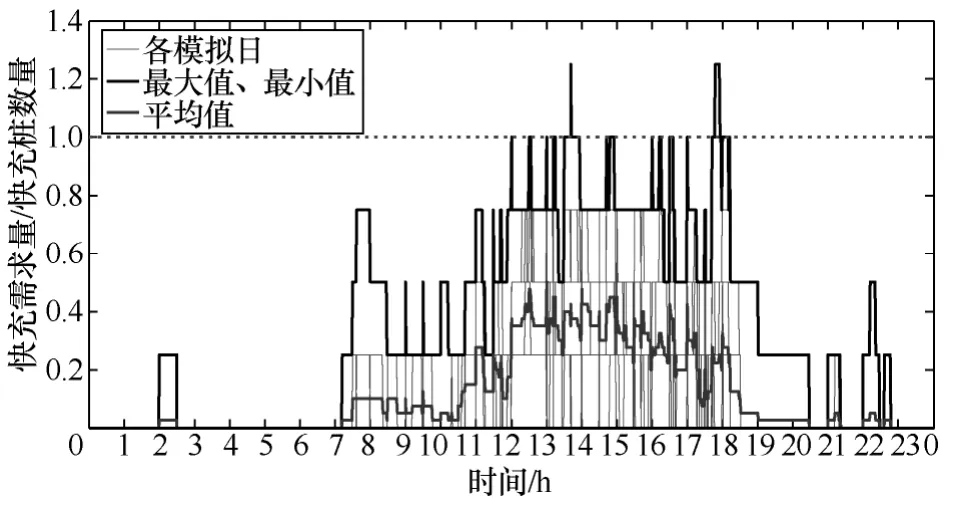
图8 商业区快充需求与快充设施数量比值曲线Fig.8 curves of ratio of charging demand and quantity of fast charging piles in shopping center

表6 商业区快充需求满足情况Tab.6 Results of verification for fast charging

从以上验证分析结果可以看出，在10个模拟天数内，商业区和休闲区的平均日需求满足率达到95%以上，部分模拟日达到100%，表示所建充电桩数量可以满足一日内绝大部分车辆即到即充的需求，工作区相对其他区域满足率较低，但均值也达到94.4%，最高一日达到99.4%，接近100%。

在峰值需求适应力方面，商业区和休闲区部分模拟日可完全满足日峰值需求，部分模拟日会有少量车无法即到即充，工作日充电桩对峰值需求的满足程度相对其他区域较差，这是由于工作区停车时刻相对集中，而本文车桩比计算是以区域平均停车时长内停车数量为基数。

商业区快充需求可以得到较好满足，日均需求满足度接近99%，10 日内仅2 日快充需求不能得到完全满足，且均只有1 辆车不能及时得到快充补充。

从验证结果可以看出，本文所提充电设施配比度方法可以较好满足用户充电需求。值得注意的是，本文模拟验证的是充电桩配置对用户即到即充需求的满足情况，并未考虑用户对充电时间的自主调控。实际上，用户可通过合理安排充电时间，避开充电最高峰阶段，在充电桩空余期为电动汽车补充电能，形成有序充电，从而降低峰值需求，提升充电桩的利用率。这对于停车周期较长的工作区、休闲区而言是非常可取的。

5 结论

本文基于对用户行驶规律统计数据的分析，提出了电动汽车分散充电设施配比度计算方法:以用户对剩余SOC 的不同心理承受能力为条件，对各个功能区充电需求概率进行了统计分析，从而确定电动汽车与慢充桩的配比度；以用户慢充充电单次补充的电能能否满足下一次行驶需求作为是否有快充需求的判断条件，计算得到快充需求概率，从而确定待研区域内快慢充配比度。最后提出了考量配比度满足充电需求程度的指标，并通过模拟电动汽车的充电行为对本文配比度进行了验证。结果表明，对于待研区域内一定数量的电动汽车，根据本文所提方法可确定两类分散充电设施的相对合理配置数量，对充电设施的规划布局的研究具有指导意义。

不同城市或区域内的电动汽车在行驶及充电行为方面规律不尽相同，因此，在使用本文方法确定分散充电设施建设数量时，应在目标区域进行实地调研和数据采集，使规划方案更加符合该地区的实际情况。

[1]吴憩棠.我国“十城千辆”计划的进展[J].新能源汽车,2009,1(24):15-19.Wu Qitang.Progresses in“Ten cities &thousand units”plan[J].New Energy Vehicles,2009,1(24):15-19.

[2]关于继续开展新能源汽车推广应用工作的通知[EB/OL].[2013-9-17].http://www.miit.gov.cn/n11293472/n11293832/n12843926/n13917042/15629217.html.

[3]四部委确定第一批新能源汽车推广应用城市或区域名单[EB/OL].[2013-11-26].http://gs.mof.gov.cn/lanmudaohang/zhengcefagui/201311/t20131126_1016 791.html.

[4]李菱,李燕青,姚玉海,等.基于遗传算法的电动汽车充电站的布局规划[J].华东电力,2011,39(6):1004-1006.Li Ling,Li Yanqing,Yao Yuhai,et al.Layout planning of electric vehicle charging stations based on genetic algorithm[J].China Electric Power,2011,39(6):1004-1006.

[5]唐现刚,刘俊勇,刘友波,等.基于计算几何方法的电动汽车充电站规划[J].电力系统自动化,2012,36(8):24-30.Tang Xiangang,Liu Junyong,Liu Youbo,et al.Electric vehicle charging station planning based on computational geometry method[J].Automation of Electric Power Systems,2012,36(8):24-30.

[6]刘志鹏,文福拴,薛禹胜,等.电动汽车充电站的最优选址和定容[J].电力系统自动化,2012,36(3):54-59.Liu Zhipeng,Wen Fushuan,Xue Yusheng,et al.Optimal siting and sizing of electric vehicle charging stations[J].Automation of Electric Power Systems,2012,36(3):54-59.

[7]高赐威,张亮,薛飞,等.集中型充电站容量规划模型研究[J]中国电机工程学报.2012.32(31):27-34.Gao Ciwei,Zhang Liang,Xue Fei,et al.Study on capacity and site planning of large-scale centralized charging stations[J].Proceedings of the CSEE,2012,32(31):27-34.

[8]李国,张智晟,温令云.换电模式下电动汽车充换电网络的规划[J].电力系统保护与控制,2013,41(20):93-98.Li Guo,Zhang Zhisheng,Wen Lingyun.Planning of battery-switching and vehicle-charging network based on battery switching mode[J].Power System Protection and Control,2013,41(20):93-98.

[9]SAE.SAE J1772 SAE Electric Vehicle and Plug in Hybrid Electric Vehicle Conductive Charge Coupler[S].SAE,2012.

[10]全国汽车标准化技术委员会.GB/T 20234.1－2011电动汽车传导充电用连接装置 第 1 部分:通用要求[S].北京:中国标准出版社,2011.

[11]全国汽车标准化技术委员会.GB/T 20234.2－2011电动汽车传导充电用连接装置 第 2 部分:交流充电接口[S].北京:中国标准出版社,2011.

[12]全国汽车标准化技术委员会.GB/T 20234.3－2011电动汽车传导充电用连接装置 第 3 部分:直流充电接口[S].北京:中国标准出版社,2011.

[13]尹政,张鹏波,杨永广,等.车用锂电池充电技术综述[J].内燃机与动力装置,2010,3:1-6.Yin Zheng,Zhang Pengbo,Yang Yongguang,et al.Charging technique of vehicle’s Li-ion battery[J].Journal of Power Sources,2010,3:1-6.

[14]王雪非.基于工况仿真的锂动力电池寿命研究[D].哈尔滨:哈尔滨理工大学,2011.

[15]张佩.车用动力电池组效率特性研究[D].武汉:武汉理工大学,2012.

[16]上海电动汽车示范运行一周年数据分析[EB/OL].[2012-7-27].http://www.evdays.com/html/201207/37589.html.

[17]John Smart,Stephen Schey.Battery electric vehicle driving and charging behavior observed early in the EV project[J].SAE International Journal of Alternative Powertrains,2012,1(1):27-33.