应用多重分形奇异值分解 (MSVD)技术提取钦杭成矿带南段文地地区Cu-Pb-Zn矿致地球化学弱异常*

吕文超，周永章，朱本铎

(1.国土资源部海底矿产资源重点实验室//广州海洋地质调查局，广东广州 510075;2.中山大学地球科学系，广东广州 510275）

钦杭成矿带位于杨子板块与华夏古板块的结合带，南自钦州湾，北至杭州湾，全长2000 km，宽100 ～150 km，总体呈反 S 状弧型分布［1－2］。它是极富特色的成矿域，拥有巨大的多金属找矿潜力。

本研究区为钦杭成矿带南段文地幅地区，有重要的成矿潜力，已发现多个金属矿床，包括金山银金矿、廉江银金矿、澳通铅锌矿、君山铅锌矿、禾寮锌矿等［3－5］，是重要的Cu-Pb-Zn多金属成矿区。尽管前人做过一定程度的地质勘查研究［6－8］，但由于该区第四纪沉积物覆盖较厚，隐伏矿体的Cu-Pb-Zn引起的地球化学异常十分微弱，阻碍了应用地球化学异常对该区Cu-Pb-Zn矿床的寻找。

多重分形是研究具有空间统计自相似性及分形结构在空间上的一种多重镶嵌的一种结构，成矿过程产生的地球化学异常就具有这种多重分形分布的特征［9－10］。奇异性过程指在相对较短的时间或者空间内产生物质的超常富集、堆积或者巨量能量释放的一种过程，这种过程在自然界中普遍存在，比如火山喷发、暴风雨、滑坡、森林大火、洪水等［11－13］。成矿过程也是一种奇异性过程，在其过程中所产生的矿床、矿致异常可以用幂率函数来度量，具有分形和多重分形的规律［9－10，14－16］。奇异性分析的目的就是在多次叠加、共同作用的复杂地质过程中，深层次挖掘出与成矿过程有关的信息。

前人研究显示［17－19］，奇异值分解 (SVD)可以应用在垂直地震剖面中上行波、下行波和噪声的分离，计算探地雷达图像波反射总量，对噪声和信号进行分离等。它是作为线性代数中用于矩阵分解中的一项重要方法，可以将数据集分解成一系列特征子空间。成矿过程是在一定时间和空间内的物质超常堆积和富集，这往往使得成矿作用结果的一些异常表现集中在一些相应的特征子空间中，这些特征子空间的能量与特征值平方之间的关系符合分形和多重分形分布，因此，应用分形分布的幂率函数可将不同特征子空间进行分离，可以更好的提取出与矿化有关的弱异常信息［20］。

1 多重分形奇异值分解技术原理

奇异值分解是在代数理论中非常有用的一种方法，它是将矩阵分解成左特征向量矩阵、对角矩阵和右特征向量矩阵的乘积。地球化学数据可以看作为一个矩阵X(m，n)。依据奇异值分解理论，可以进行如下分解:

其中，U为左特征向量矩阵，S为对角矩阵，也即奇异值矩阵，V是右特征向量矩阵，T代表矩阵的转置。矩阵S中的数值即为矩阵X的奇异值，且沿对角线降序分布，这些奇异值的分布符合分形和多重分形分布，可以用幂率函数描述［10，20－23］，其值大小为矩阵XXT或XTX特征值的正平方根，即

其中，r为矩阵X的秩，σ1≥σ2≥…≥σr＞0，σi=奇异值矩阵分解还可以写成如下的形式:

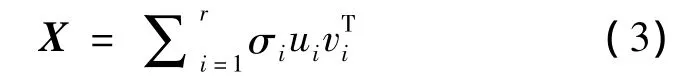
式中，r是矩阵X的秩，σi是矩阵X的第i个特征值，ui和vi分别是XXT和 XTX的第i个特征向量，是一个m×m阶矩阵，是原始矩阵X的第i个特征子空间。因此，应用式3可以应用全部的特征值重构出原始矩阵X，那么选取部分特征值进行重构，则将重构出含有原始矩阵部分信息的特征子空间。但是如何选取不同的奇异值来重构其对应的子空间是重建原始场，提取异常场的关键。前人通过研究［9］:这些特征值在双对数图中存在不同的多重分形特征 (幂率关系)，依据曲线的不同斜率，用不同的直线段分别对曲线拟合，不同线段的交点即为重构中的分界点。

综上所述，MSVD方法就是首先将地球化学数据看作为一个矩阵X(m，n)，其次应用基于MATLAB平台编制奇异值矩阵分解程序分解出奇异值矩阵，然后应用多重分形方法确定奇异值矩阵的分界点，最后再应用MATLAB软件编制的程序进行重构不同的特征子空间，奇异值所重构出的特征子空间往往与一定的地质过程相对应，以此达到异常场与区域场分离的目的。

2 MSVD对文地地区CuPbZn矿致地球化学弱异常的识别

2.1 研究区区域地质特征

前人曾对1∶50000文地幅所在的区域开展过一定的区域地质调查和研究［6－8，16］。这些前期工作为认识研究区的区域地质特征奠定了重要的基础。结合前人研究成果和本研究地质测量工作发现(图1)，该区出露的地层有白垩系和第四系，岩浆岩以酸性侵入岩为主，包括了研究区北部的茶子窝岩体和中部的英桥岩体。研究区混合岩大面积发育，岩性为均质混合岩、眼球状混合岩、混合质片岩和混合花岗岩。该区构造线方向整体上呈北东向，两条最大的北东向构造线为彭西垌－金坑断裂带和文地背斜。

图1 文地区域地质图Fig.1 Regional geological map of Wendi

2.2 CuPbZn地球化学矿致弱异常信息提取

本研究开展了研究区1∶50000水系沉积物的采样和地球化学分析工作。采样密度和采样布局严格按中国地质调查规范进行。平均采样密度4.27个/km2。将1 km2作为一大格，每一大格又分为4个0.25 km2的小格，严格控制在一个大格或连续5个以上小格没有采样点的情况出现。采样物质以淤泥和粉细砂为主。采样重量以过60目筛后达200 g为原则。

样品分析送由江西省地球物理地球化学实验测试所完成。分析项目为 Cu、Pb、Zn、Mn、Sn、W、Ag、Au、As、Sb、Bi、Mo、Hg、F 、Ba 和 B等16种。表1列出了用于本研究的Cu、Pb、Zn三种元素的此次测试分析方法、检出限和报出率。

图2(a)展示了Cu元素lnλ－lnE对数图。根据特征值空间能量百分比和奇异值平方之间在不同区段之间存在的不同幂率关系，确定了3个区间。它们分别为λ1－λ3、λ4－λ23和大于λ23的3部分。λ1－λ3重构的空间能量所占总能量比例90%以上，反映的是区域Cu异常;λ4－λ23重构的空间反映的是局部矿致Cu异常;大于λ23的那部分能量所占百分比微忽其微，可能是一些微弱的矿致异常或者为一些各种来源的“噪声”，可以忽略。

图2(b)展示了Pb元素lnλ-lnE对数图。根据特征值空间能量百分比和奇异值平方之间在不同区段之间存在的不同幂率关系，确定了3个区间。它们分别为λ1－λ2、λ3－λ16和大于λ16的3部分。λ1－λ2重构的空间能量所占总能量比例90%以上，反映的是区域Pb异常;λ3－λ16重构的空间反映的是局部矿致Pb异常;大于λ16的那部分能量所占百分比微忽其微，可能是一些微弱的矿致异常或者为一些各种来源的“噪声”，可以忽略。

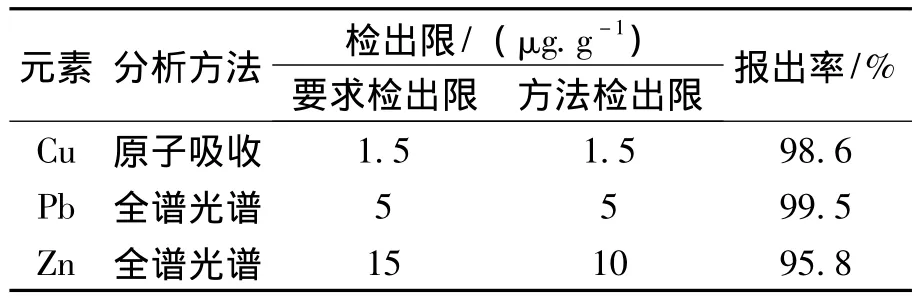
表1 分析方法和检出限Table 1 Analytical method and detection limit

应用MSVD方法对研究区1∶50000水系沉积物地球化学数据分析的步骤包括［9，20－23］:首先将研究区水系沉积物地球化学数据Cu、Pb、Zn三种成矿元素分别看作为一个二维矩阵X(m，n)，然后应用基于MATLAB平台编制奇异值矩阵分解程序分解出奇异值矩阵，再应用多重分形方法确定奇异值矩阵的分界点。

在借鉴熊德国提出的生产性生态足迹的核算公式基础上，修正方恺（2018）提出的以全球平均生物生产力核算土地足迹的生态足迹模型，本文给出生物生产型生态足迹计算公式：

图2 Cu、Pb、Zn元素ln λ-lnE对数图Fig.2 ln λ vs lnE for Cu-Pb-Zn

图2(c)展示了Zn元素lnλ－lnE对数图。根据特征值空间能量百分比和奇异值平方之间在不同区段之间存在的不同幂率关系，确定了3个区间。它们分别为λ1－λ2、λ3－λ21和大于λ21的3部分。λ1－λ2重构的空间能量所占总能量比例90%以上，反映的是区域Zn异常;λ3－λ21重构的空间反映的是局部矿致Zn异常;大于λ21的那部分能量所占百分比微忽其微，可能是一些微弱的矿致异常或者为一些各种来源的“噪声”，可以忽略。

本研究应用MATLAB软件编制的程序对研究区Cu、Pb、Zn数据进行重构不同的特征子空间。

图3(a)为Cu元素λ1－λ3重构的空间，反映的是区域Cu异常。图3(b)为Cu元素λ4－λ23重构的空间，反映的是局部矿致Cu异常。

图3(c)为Pb元素λ1－λ2重构的空间，反映的是区域Pb异常。图3(d)为Pb元素λ3－λ16重构的空间，反映的是局部矿致Pb异常。

图3(e)为Zn元素λ1－λ2重构的空间，反映的是区域Zn异常。图3(f)为Zn元素3－21重构的空间，局部矿致Zn异常。

图3 Cu-Pb-Zn元素异常图Fig.3 The anomaly map of Cu-Pb-Zn elements

从以上各图展示的分析结果可以看出，对Cu、Pb、Zn来说，尽管该区的铅锌矿上覆盖层非常厚，整个原生成矿系统均被上覆盖层掩埋，但经过MSVD提取的异常依然与铅、锌、铜等矿床 (点)吻合程度甚高。这说明了MSVD方法对本研究区隐伏矿床的弱致矿异常信息的提取是有效的。

3 MSVD方法与传统方法的对比

将传统统计方法确定的异常下限成异常图并与MSVD方法所做的异常图进行比较 (图4)。

图4 传统方法和MSVD方法确定的Cu-Pb-Zn异常图Fig.4 The Cu-Pb-Zn anomaly maps obtained by traditional and MSVD method

从以上的对比图可以看出，在Cu、Pb、Zn异常方面，应用传统统计方法圈定的结果，异常与Cu、Pb、Zn矿床并不吻合，矿点地区并未有异常出现。而应用MSVD方法圈定的结果，异常与Cu、Pb、Zn矿非常吻合。

通过实地野外地质填图发现，研究区的铅锌矿上覆盖层非常厚，整个原生成矿系统被上覆盖层掩埋，只能通过长期的地质系统的作用下，隐伏的成矿系中所富集的成矿元素和微粒矿物质才有可能在覆盖层中富集，形成弱异常。然而，研究区的Ag、Au矿Pb、Zn元素含量也比较高，而Ag、Au矿受断裂带控制。在研究区地表多见Ag、Au矿化脉的出露，Ag、Au矿化脉长期的风化剥蚀作用，不仅导致了Ag、Au异常的形成，也造成了Pb、Zn的高背景值，因此也影响了Pb、Zn较弱的矿致异常的识别，所以异常的识别和圈定相对较难。因此，微弱但有用的深部源致矿异常信息往往由于简单的统计方法的使用而漏掉。

Cu、Pb、Zn致矿异常的提取表明，MSVD技术能够克服Ag、Au矿引起的Cu、Pb、Zn高背景的影响，并从多重地球化学背景中有效提取致矿异常，包括低背景中的弱异常和隐蔽异常。该方法揭示了一系列Cu、Pb、Zn统计方法圈定的异常图上没有显示的、规模不等的矿化异常，其中的一些异常和一系列矿床、矿点、矿化点重和，在未知区得到的弱异常也有进一步开展工作的意义，这为该区矿床勘查提供了新的靶区，为未知矿床的探寻提供了新的启示。

4 结论

矿床的形成是复杂的地质过程和矿化过程的产物，而矿化过程往往具有多期次性，每一矿化期次都有可能导致地球物理和地球化学异常，导致了地球化学特征无论在平面上，还是在垂向上，宏观上，还是微观上，都呈现不均匀性，这使得地球化学空间分布格局上具有多重分形和奇异性的特征。而MSVD方法不是一个简单的数学概念，它是能够深入刻画成矿过程的多重分形和奇异性特征的数理模型，与传统方法相比，这种方法不仅可以研究地球物理场和地球化学场空间分布特征，而且可以区分地球化学场的背景以及与矿化有关的异常场。

本研究应用MSVD技术对研究区的1∶50000水系沉积物地球化学数据进行分析，表明该方法可以细致的刻画研究区与矿化有关的局部地球化学异常特征，可以更加有效抑制非矿引起的地球化学高背景，更深层次提取Cu、Pb、Zn弱矿化异常信息。

［1］杨明桂，梅勇文.钦－杭古板块结合带与成矿带的主要特征［J］.华南地质与矿产，1997，9(3):52－59.

［2］周永章，曾长育，李红中，等.钦州湾－杭州湾结合带(南段)地质演化和找矿方向［J］.地质通报，2012，31(2/3):32－37.

［3］周永章，曾长育，李红中，等.钦杭成矿带典型矿种及其矿床分布总体特征［J］.矿床地质，2010，29(增刊):34.

［4］吕文超，李红中，安燕飞，等.矿产资源定量预测的研究进展［J］.矿床地质，2010，29(增):755.

［5］吕文超，杨志军，周永章，等.钦杭结合带南段和寮铅锌多金属矿床石英的谱学特征及其指示意义［J］.光谱学与光谱分析，2013，33(5):1374 －1378.

［6］广东省地质矿产局.广东省区域地质志［M］.北京:地质出版社，1988:941.

［7］广西状族自治区地质矿产局.广西壮族自治区区域地质志［M］.北京:地质出版社，1985:853.

［8］广西壮族自治区地质矿产局.1∶5万区域地质调查报告(文地幅和石角幅)［M］.北京:地质出版社，1985:145.

［9］成秋明，赵鹏大，陈建国，等.奇异性理论在个旧锡铜矿产资源预测中的应用:成矿弱信息提取和复合信息分解［J］.地球科学—中国地质大学学报，2009，34(2):232－242.

［10］成秋明，赵鹏大，张生元，等.奇异性理论在个旧锡铜矿产资源预测中的应用:综合信息集成与靶区圈定［J］.地球科学—中国地质大学学报，2009，34(2):243－252.

［11］CHENG Q M.Non-linear theory and power-law models for information integration and mineral resources quantitative assessments ［J］.Mathemathecal Geosciences，2008，40:503－532.

［12］CHENG Q M，AGTERBERG F P.Singularity analysis of ore-mineral and toxic trace elements in stream sediments［J］.Computer＆ Geosciences，2009，35:234 －244.

［13］CHENG Q M，ZHAO P D.Singularity theories and methods for characterizing mineralization processes and mapping geo-anomalies for mineral deposit prediction［J］.Geoscience Frontiers，2011，2(1):67－79.

［14］张焱，成秋明，周永章，等.分形插值在地球化学数据中的应用［J］.中山大学学报:自然科学版，2011，50(1):133－137.

［15］张焱，周永章，黄锐，等.粤北刘家山地区多元素分形维数谱函数及其对矿化的指示分析［J］.中山大学学报:自然科学版，2012，51(2):119 －124.

［16］吕文超，周永章，张焱，等.钦杭成矿带南段文地幅水系沉积物地球化学异常识别［J］.中山大学学报:自然科学版，2012，51(5):107－112.

［17］FREIRE S L M，ULRYCH T J.Application of singular value decomposition to vertical seismic profiling［J］.Geophysics，1988，53:778 －785.

［18］CAGNOLI B，ULRYCH T.Singular value decomposition and wavy reflections in ground-penetrating radar images of base surge deposits［J］.Journal of Applied Geophysic，2001，48:175－182.

［19］VRABIE V D，MARS J I，LACOUME J L.Modified singular value decomposition by means of independent component analysis［J］.Signal Process，2004，84:645－652.

［20］李庆谋，成秋明.分形奇异(特征)值分解方法与地球物理和地球化学异常重建［J］.地球科学—中国地质大学学报，2004，29(1):109－118.

［21］CHENG Q M.Multifractal distribution of eigenvalues and eigenvectors from 2D multiplicative cascade multifractal fields［J］.Mathematical Geology，2005，37:915－927.

［22］ZHAO B B，CHEN Y Q.Singular value decomposition(SVD)for extraction of gravity anomaly associated with gold mineralization in Tongshigold field，Western Shangdong Uplifted Block，Eastern China［J］.Nonlinear Processes in Geophysics，2011，18:103 －109.

［23］WANG G W，ZHANG S T，YAN C H，et al.Application of the multifractal singular value decomposition for delineating geophysical anomalies associated with molybdenum occurrences in the Luanchuan ore field(China)［J］.Journal of Applied Geophysics，2012，86:109 －119.

［24］HAWKES H E，WEBB J S.Geochemistry in mineral exploration［M］.New York:Harper and Row，1962.

［25］黄瑞.化探数据处理方法研究——以攀西地区铂族元素为例［D］.成都:成都理工大学，2005.

［26］李河江.若尔盖地区地球化学异常数据处理研究［D］.成都:成都理工大学，2006.