应用于月度用电量预测的小波分析法

吴雪花

(南京航空航天大学金城学院，江苏南京 211156)

月度用电量预测是中期负荷预测的主要内容，也是制定月度发电规划的基础。近年研究发现，用电量不仅呈逐年变化的趋势，而且受气温波动的影响[1]。因此将月度用电量数据逐年变化趋势的特征和随气温波动的特征这2 种特征进行分离剖析，能够提高预测的准确性[2，3]。小波分析法是一种运用伸缩平移运算，对高频分量进行时间细分，低频分量进行频率细分，最终将信号分解成一系列小波函数叠加的分析方法。该方法实现了时间频率的局部化分析。相较于傅里叶分析，小波函数可以逼近非稳态信号中尖锐变化的部分，也可以逼近离散不连续具有局部特性的信号，描述能力更强，是信号分解的一种常用方法，对非线性信号具有较好的分解效果[4]。

文献[3]采用小波分析法，将用电量数据分解成若干不同尺度的分量，使得数据逐年变化趋势的特征和随气温波动的特征这两种特征分离，然后采用BP神经网络对各分量分别进行预测，总体预测精度更高。然而小波分析每进行一次分解，小波系数的采样点会减少一半，影响预测精度，文献[3]并未对小波分解的这种不足加以分析。

针对这种不足，本文将做如下改进：首先采用小波分析法对月度用电量进行分解；然后采用小波重构将各小波系数恢复到原数据的长度；最后采用RBF神经网络对恢复长度的各系数进行月度用电量预测，并与传统的小波分析法进行比较。

1 小波分析法

1989年，Mallat 等人采用滤波器的方法实现了离散小波变换[4]，Mallat 离散小波变换可表示为：

式（1，2）中：j为分解尺度；k，n为平移系数；cAj为第j 层小波系数的低频部分；cAj+1和cDj+1分别为第j+1 层小波系数的近似分量和细节分量；H，G为小波分解滤波器。

式（1）和式（2）所示的离散小波变换等效于分别采用高通滤波器H 和低通滤波器G 对cAj进行滤波，并进行降采样，得到近似分量cAj+1和细节分量cDj+1。

形象化的小波分解过程如图1 所示。首先对原信号x（t）进行小波变换，即对x（t）进行滤波和降采样，得到近似分量cA1和细节分量cD1；然后对近似分量cA1进行小波变换，即对cA1进行滤波和降采样，得到cA2和cD2；接着对近似分量cA2进行小波变换，……，以此类推，直至得到近似分量cAj+1和细节分量cDj+1。

图1 小波分解的流程图

文献[3]中采用小波分析法，将原信号x（t）进行3次滤波和降采样，得到相应的近似分量和细节分量。其中近似分量表征逐年变化趋势的特征，细节分量表征随气温波动的特征。然后采用组合预测的方法，利用小波系数cD1，cD2，cD3和cA3，对波动分量和趋势分量分别进行预测。然而，这种仅利用小波系数cD1，cD2，cD3和cA3进行组合预测的方法存在2个缺点。

（1）各小波系数中横坐标为采样点，纵坐标为系数值，缺乏具体的物理意义。

（2）在离散小波分解过程中，每进行一次滤波和降采样，采样点就会减少一半。如果原信号数据有269个采样点，那么，经4 次滤波和降采样后得到的cA4仅剩17个采样点，显然会降低表征逐年变化趋势的特征分量的预测精度。

为了克服上述缺点，可以对小波系数cD1，cD2，cD3，cD4和cA4分别进行重构，使得它们恢复原来的数据长度。借助Mallat 离散小波变换对应的反变换，可以有效实现该重构目标。Mallat 离散小波变换对应的反变换可表示为：

式（3）中：H'，G'为小波重构滤波器，且H'为高通滤波器，G'为低通滤波器。

式（3）表示的离散小波反变换等效于采用低通滤波器G'对近似分量cAj+1进行滤波，同时采用高通滤波器H' 对细节分量cDj+1进行滤波，然后对这2个输出量进行求和并升采样，重构得到上一层小波系数的低频部分cAj。升采样过程中要在各系数各采样点之间插零，并通过重构滤波器H'，G'进行滤波。形象化的小波分解和重构的全过程如图2 所示。

图2 月度用电量数据小波分解的全过程

通过小波重构，各小波系数不仅恢复了原来的长度，且都被赋予了明确的物理意义，D1，D2，D3，D4和A4可以看作是原信号x（t）的4个分量，并且有：

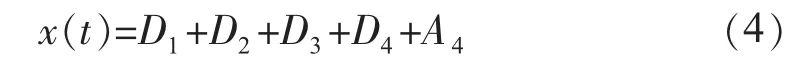
小波函数决定着小波变换及其反变换过程中各滤波器H，G，H'，G'的表达式，其选取直接关系着分解效果的好坏。Daubechies 是一类正交小波函数，在分解的过程中不会造成信息的丢失，因此被广泛应用于负荷预测领域。

2 算例分析

以美国亚利桑那州从1990年1 月至2007年5 月共209个月的月用电量数据为例，该数据来自美国能源信息局官方网站：http://www.eia.gov/electricity/data.cfm。数据曲线如图3 所示。其中，前173个月的数据用于训练，后36个月的数据用于测试。本文进行月度用电量预测方法的流程图如图4 所示。

图3 亚利桑那州1990年1 月至2007年5 月月度用电量曲线

图4 本文预测方法的流程图

首先对月度用电量数据x（t）进行小波分解，4 次滤波和降采样之后，再通过小波重构恢复数据长度，得到D1，D2，D3，D4和A4的5个分量；然后对D1，D2，D3，D4和A4分别采用RBF 神经网络进行预测，本次预测模型需要建立5个RBF 神经网络；最后对5个预测结果进行求和，得到预测值。具体的，首先采用Daubechies 4 小波函数，将亚利桑那州月用电量数据进行小波分解，结果如图5 所示。

从图5 中可以看出，第4 次小波变换后，近似分量cA4已基本没有波动的特征，因此可以认为系数cA4代表了月度用电量数据中不随气温变化的那一部分趋势分量，此外的cD1，cD2，cD3和cD4，与cA4相对应，是反映月度用电量数据随气温波动的那一部分分量。

经过小波分解，原信号x（t）中不同尺度的分量已基本被分离出来，在此基础上对各分量进行对应的小波重构，使得各分量恢复原来的数据长度。重构后的各分量分别为D1，D2，D3，D4和A4，它们的曲线图如图6所示。

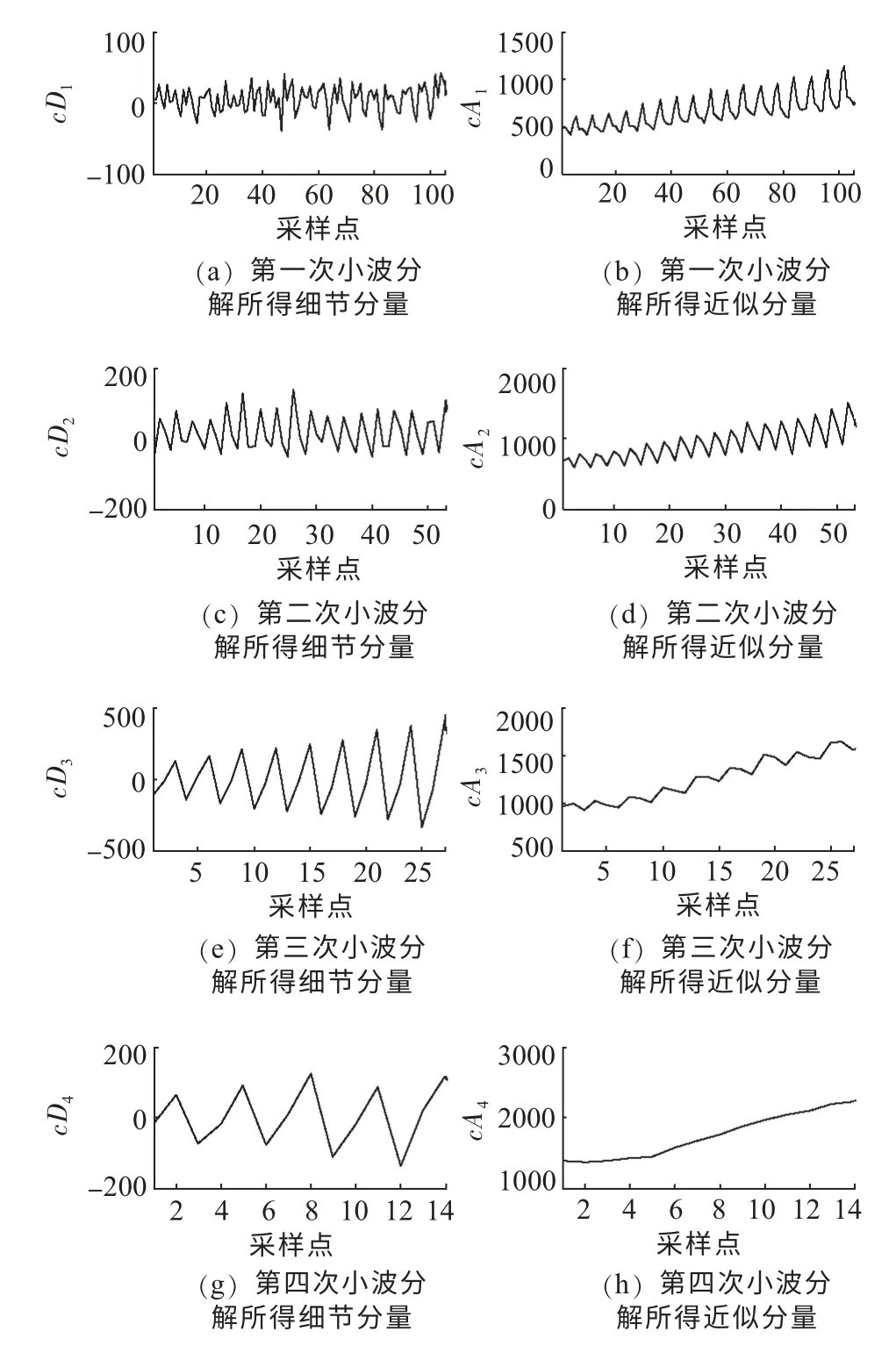
图5 月度用电量曲线小波分解结果

获得上述分析结果后，就可以对未来一个月的用电量值进行预测了。虽然月度用电量数据受到气温、经济、政治等因素的影响，但是这些因素大多以12个月为周期，因此采用过去12个月的月用电量数据来预测未来一个月的用电量是非常合理的[5，6]。本文采用RBF神经网络对上述分析结果进行预测。RBF 神经网络是一种三层前馈网络，具体的结构图如图7 所示。图中x（tp-1），x（tp-2）…x（tp-12）为所需预测月度tp之前连续12个月的用电量数据，而xpre（tp）为该月度用电量的预测值。

本次算例中，需要建立5个如图7 所示的RBF 神经网络，依次命名为RBFNN1～5。然后，将恢复原来数据长度的小波系数D1，D2，D3，D4和A4作为历史数据，分别输入RBFNN1～5 中，每个小波系数对应一个RBF 神经网络。譬如，将D1中前173个月的数据每连续12个月作为一组输入RBF 神经网络RBFNN1 中，预测相应未来一个月的用电量，预测值输出量结合对应月份已知用电量可以训练RBFNN1。利用训练好的神经网络RBFNN1 预测小波系数D1中后36个月的数据D1pre（i），其中变量i为1～36的自然数。参照以上步骤，分别预测D2，D3，D4和A4中后36个月的数据，分别为D2pre（i），D3pre（i），D4pre（i），A4pre（i），其中变量i为1～36的自然数。D1pre（i），D2pre（i），D3pre（i），D4pre（i）和A4pre（i）是后36个月的预测用电量xpre（i）的5个分量，并且有：

图6 小波重构后恢复原来数据长度各分量

图7 RBF 神经网络结构图

MATLAB 仿真结果显示，本文提出的方法预测精确度较高。为了充分说明这点，接下来将采用另外2 种方法进行预测对比。其中，方法1 不对月度用电量数据x（t）做任何分解，直接采用RBF 神经网络对x（t）进行预测；方法2 采用文献[3]提出的小波分析法对x（t）进行预测；方法3 是本文提出的方法。3 种方法的36个月用电量数据预测结果如图8 所示。

图8 各预测方法预测结果

从图8 中可以看出，相比于其他2 种方法，本文所提出的方法具有更高的预测精度。为进一步比较上述3 种方法的预测精度，还可以比较它们预测结果的2个指标。

平均绝对百分误差：

均方根误差：

式（6，7）中：N为测试样本的个数，这里为36个；x（i）为实际值；xpre（i）为预测值。3 种方法的平均绝对百分误差δMAPE和均方根误差δRMSE如表1 所示。

从表1 可以看出，方法3的δMAPE和δRMSE比另外2种方法要小，再一次证明了本文所提出的方法对月度用电量数据的预测更加精确。

表1 3 种方法的预测误差

3 结束语

本文提出了一种应用于月度用电量预测的小波分析法。传统的Mallat 小波分析法在小波分解过程中，每进行一次分解，采样点就会减少一半，从而影响预测精度。针对这种现象，该法可以通过小波重构将各分量的采样点个数恢复到原来数据的长度，再通过RBF 神经网络进行预测，大大提高预测精度。

[1]许 琦，曾 凌.南京电网负荷与气温敏感性分析[J].江苏电机工程，2012，31(5)：55-57.

[2]刘学琴，吴耀华，崔宝华.小波软阈值去噪和GRNN 网络在月度负荷预测中的应用[J].电力系统保护与控制，2009，37(14)：59-62.

[3]姚李孝，刘学琴.基于小波分析的月度负荷组合预测[J].电网技术，2007，31(19)：65-68.

[4]MALLAT S.A Theory for Multiresolution Signal Decompositionthe Wavelet Representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(7)：674-693.

[5]CHEN Y,LUH P B,GUAN C.Short-Term Load Forecasting:Similar Day-Based Wavelet Neural Networks[J].IEEE Transactions on Power Systems,2010,25(1)：322-330.

[6]AGNALDO R R,ALEXANDRE P A.Feature Extraction via Multiresolution Analysis for Short-term Load Forecasting[J].IEEE Transactions on Power Systems,2005,20(1)：189-198.