臂式输弹机强制行程内弹丸姿态分析＊

刘朋展，薄玉成，王惠源，张鹏军

（中北大学 机电工程学院，山西 太原 030051）

目前输弹机常用的输弹方式有强制输弹和弹射输弹两种，采用弹射输弹时弹丸具有较大的初速，所以输弹时间短，有利于提高火炮射速，但弹射输弹时弹丸姿态的稳定性对输弹可靠性的影响较大.文献［1-3］中叙述了输弹机的发展现状，文献［4-12］中叙述了输弹机设计中的一些方法和需要注意的问题.由于弹射式输弹方式中输弹机只有在强制段中对弹丸产生作用，弹丸在强制行程末端的姿态是最终可控量，决定了弹丸能否可靠地装填，所以对强制段中弹丸的受力情况和姿态进行了分析，以提高输弹的可靠性和一致性.

弹射式输弹机的输弹过程分为强制与惯性两个阶段.强制输弹阶段输弹机驱动弹丸完成加速过程，使得弹丸获得一定的速度.惯性输弹阶段从输弹臂与弹丸分离点开始，弹丸依靠惯性进入炮膛，在到达卡膛位置时弹丸依靠动能挤入膛线结束.本文分析的臂式输弹机结构如图1 所示.

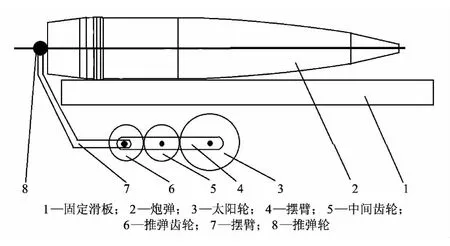
图1 臂式输弹机原理Fig.1 Theory of arm-type ramming

1 输弹过程分析与输弹力计算

在输弹过程中，太阳轮与固定滑板保持不动，摆臂在驱动力的作用下绕太阳轮回转，推弹臂与推弹齿轮是刚性连接，运动传递到推弹臂末端的推弹轮，推弹轮做一个近似直线运动推动弹丸，使得弹丸获得一定的动能，从而使炮弹装填入身管.

图2 推弹力计算原理Fig.2 Theory of force calculate

假设在角度一定时，臂式推弹机推弹轮处的推弹力是恒定的，推弹力作用点在炮弹尾部中心，推弹力方向平行于弹丸轴线，弹丸在输弹槽上滑动，摩擦系数μ2 ＝0.05.假设在炮弹进入身管后只与身管发生滑动摩擦，其摩擦系数μ1 ＝0.22.其原理图如图2 所示.

需要的推弹力有以下关系：

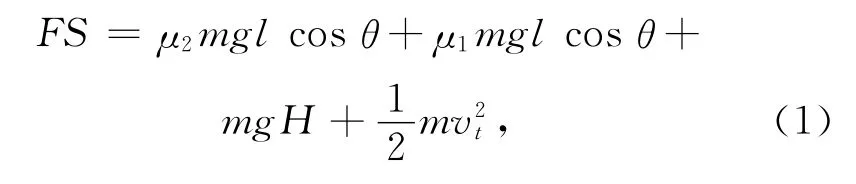
式中：F为推弹力；θ为射角；S为推弹行程；vt为炮弹的卡膛速度；L为炮弹在身管内的行程；m为弹丸质量；l为炮弹在输弹槽上的行程；H为炮弹从初始位置到终点上升的垂直高度.

以某火炮为例，取参数值为：S＝0.3 m，L＝0.6 m，l＝0.8 m，H＝1.7sinθ，v0＝3m／s，m＝21.5kg.编写Matlab 程序计算得到推弹力随射角变化的曲线，如图3 所示.

图3 推弹力变化Fig.3 Change of ramming force

当推弹点偏离弹丸轴线位置时，推弹力方向与弹丸质心运动方向不在一条直线上，弹丸上会产生力矩.弹丸是靠本身重力放置在输弹槽上的，当力矩较大时，弹丸会在竖直方向有转动，即弹丸会发生头部翻转或者尾部翘起.输弹槽为V 型槽，弹丸轴线垂直方向的位移被限制，当推弹力在此方向上偏离推弹质心时，不会影响弹丸的姿态，因此可忽略不计.

图4 弹丸受力分析图Fig.4 Force analysis of cannonball

当推弹力偏离弹丸形心位置向下时，会使弹丸产生翻转力矩，如图4 所示.当弹丸放置在V型槽上时，弹丸上弹带与定形部与V 型槽接触定位，将模型简化为弹丸在V 形槽上的支撑点有两个于A和B.当B点对V 形槽的压力为零时，弹丸处与翻转的临界状态，此时的推弹力为临界推弹力.在推弹力偏心距为e时，临界力F有以下关系：

取偏心e＝0.02 m，其中m＝21.5kg，g＝9.8，l2＝0.2m.编写Matlab 程序计算在各个角度的临界推弹力，并将推弹力（实线）与临界力（虚线）进行比较（如图5 所示），得出在输弹角度大于等于52°时，弹丸将发生翻转.

图5 推翻力与推弹力比较Fig.5 Force compare of ramming and rolling-over

由以上分析可知，当推弹点在弹丸中心以下时，射角越高，弹丸越容易发生翻转.弹丸的翻转会产生弹丸轴线与身管轴线的偏角，当弹丸装填入身管时，此偏角会引起弹丸与身管的撞击，从而影响弹丸的装填可靠性与一致性.当弹丸翻转角度较大装填时，炮弹头部会撞击到炮管尾部，如果是实弹射击的话就会造成重大事故，试验中就发生过这种情况.弹丸与身管的碰撞效果如图6 所示.

图6 弹丸与身管的碰撞效果Fig.6 Impact result of cannonball and cannon

在恒力推弹情况下，要保证弹丸在0°～70°时不发生翻转，则推弹偏心e的值应小于10mm.

当推弹点位置高于弹丸中心线时，会产生使得弹丸尾部翘起的翻转力矩，称此时的推翻力为临界推翻力，计算方法与推弹点低于中心时的计算方法类似.当e＝0.01m 时，如图7 所示推弹力（实线）与临界推翻力（虚线）曲线.

由以上分析可知，当推弹点位置高于弹丸中心线超过0.01m 时，弹丸尾部可能会发生翘起，使弹丸尾部向上偏离中心线，但是偏离后，推弹轮位置下降，弹丸尾部落下.此过程中会产生很大的能量损失，但弹丸姿态不可控.

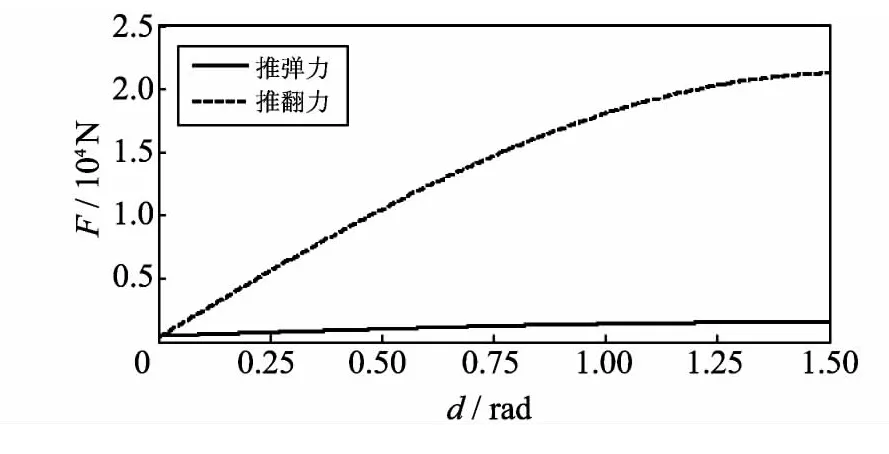
图7 推弹力与临界推翻力比较图Fig.7 Compare of ramming force and overturn force

2 模型修正

1）在实际试验中，臂式推弹机提供的推弹力并不是恒定的.输弹臂是由电机带动的，由于电机工作时间很短，要使推弹力恒定，电机的控制难度非常大.在试验中实际测得的射角为60°时电机的转速曲线如图8 所示.

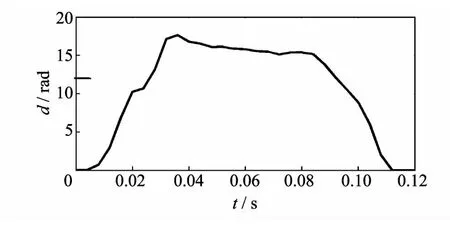
图8 电机转速曲线Fig.8 Speed of dynamo

将电机速度曲线代入ADAMS 中进行仿真，求得弹丸的加速度曲线，如图9 所示.

图9 推弹臂末端加速度曲线Fig.9 Acceleration of rammer tip

由图9 可知，在0.106s 时电机提供的加速度为整个行程中的最大值，此时的加速度是输弹滑板与推弹臂减速时的制动力提供的.在0.03s时的推弹力为整个推弹行程中的最大推弹力.将实际最大推弹力与计算出的恒力推弹力比较，得到实际最大推弹力约是恒力情况下推弹力的3.85 倍.

2）试验中推弹轮的位移曲线并不是一条直线，而是一条在一定范围内波动的曲线，机构的推弹速度、齿轮间隙与误差对推弹轮竖直方向上的位移影响较大.实际测得推弹臂末端的位移曲线为一条先下降后上升的曲线.

由于推弹点位置的上下变化，会在推弹轮与弹丸接触点产生摩擦力.此摩擦力在弹丸轴线的垂直方向上，并且与推弹轮在竖直方向上的运动方向相反.这个摩擦力会对弹丸的姿态产生影响，当推弹点位置下降时，摩擦力方向向上，产生使弹丸翻转的力矩；当推弹位置上升时，摩擦力方向向下，产生使弹丸头部翘起的阻力.

此摩擦力的影响比较小，有以下两个因素：①推弹臂末端与弹丸接触处摩擦系数较小，并且推弹轮是滚动的.②提供弹丸翻转力矩时的时间是推弹刚开始时刻，此时推弹臂末端的加速度较小，推弹力较小.为防止此摩擦力对输弹过程中弹丸的安全性产生影响，在计算过程中将弹丸翻转力矩提高10%.

考虑上述因素，通过计算得到要使弹丸在强制行程内不发生翻转的偏心距e的范围为在弹丸中心线下方0.002m 以上.此时的推弹力与推翻力比较如图10 所示.在70°射角时，推弹力（实线）为1 500N，其4倍为6 000N，考虑安全因子后为6 600N，此时临界翻转力为7 600 N（虚线），弹丸不会翻转.

图10 推弹力与推翻力比较图Fig.10 Compare of ramming force and overturn force

3 模型验证

通过高速摄影观察弹丸在强制输弹过程中弹丸的姿态，并与仿真结果进行了对比，验证了理论计算结果.高速摄影3 个时刻的推弹图如图11所示.与实际测得的数据进行比较，从弹丸姿态上看其计算结果基本符合实际.

图11 高速摄影图Fig.11 High speed photos

4 结论

通过对臂式输弹机基本结构的分析，建立了弹丸在强制行程内姿态计算的理论模型，并通过实验分析了计算结果.通过实验中发现的问题与实际机械模型的误差对理论计算模型进行了修正，得到合适的推弹点位置范围.在臂式输弹机输弹过程中，若推弹点在弹丸尾部中心位置，则弹丸姿态是稳定的.由于实际模型误差及加工、装配误差，使得推弹点会偏离弹丸尾部中心位置，这使在推弹臂末端的推弹点位置选择有了要求.通过分析得到要使得弹丸姿态保持稳定，推弹臂末端推弹点位置范围是弹丸中心线下2mm 以上，最优位置为弹丸中心线以上0.02m 处.

［1］李宗海.中大口径双管火炮自动装填系统方案研究［D］.南京：南京理工大学，2009.

［2］梁辉，马春茂，潘江峰，等.大口径火炮弹药自动装填系统研发现状和趋势［J］.火炮发射与控制学报，2010（3）：103-107.Liang Hui，Ma Chunmao，Pan Jiangfeng，et al.Current situation and development trend of auto loader in large calibre howitzer［J］.Journal of Gun Launch ＆Control，2010（3）：103-107.（in Chinese）

［3］赵森，钱勇.自行火炮半自动装填机构输弹问题研究［J］.兵工学报，2005，26（5）：592-594.Zhao Sen，Qian Yong.Ammunition ramming of semiautomatic loading device of the self-propelled gun［J］.Acta Armamentari，2005，26（5）：592-594.（in Chinese）

［4］闫纯亮，潘宏侠，刘广璞.某火炮自动装填机构参数测试结束研究［J］.机械工程与自动化，2009（6）：32-34.Yan Chunliang，Pan Hongxia，Liu Guangpu.Test technique of the technical parameters of self-loding artillery［J］.Mechanical Engineering ＆ Automation，200（6）：32-34.（in Chinese）

［5］徐灏.机械设计手册（第3卷）［M］.北京：机械工业出版社，1991：10-86.

［6］陈立平.机械系统动力学分析及ADAMS 应用教程［M］.北京：清华大学出版社，2005.

［7］李继科.火炮供输弹系统虚拟样机技术研究［D］.南京：南京理工大学，2004.

［8］樊永生.某自行火炮自动装填系统选弹器动力学仿真［J］.火炮发射与控制学报，2000（4）：34-39.

［9］哈尔滨工业大学理论力学研究室.理论力学（I）［M］.北京：高等教育出版社，2002.

［10］郑文纬，吴克坚.机械原理［M］.北京：高等教育出版社，2009.

［11］李伟，王兴贵，黄泽平.输弹机虚拟样机建模与动态仿真［J］.火炮发射与控制学报，2006（6）：29-32.Li Wei，Wang Xinggui，Huang Zeping.Modelling and dynamic simulation analysis for virtual proto type of rammer［J］.Journal of Gun Launch ＆ Control，2006（6）：29-32.（in Chinese）

［12］张鹏军，薄玉成，王惠源，等.基于小波和PCA 的火炮输弹系统故障诊断研究［J］.计算机工程与设计，2012，33（12）：4746-4750.Zhang Pengjun，Bo Yucheng，Wang Huiyuan，et al.Fault detection of gun automatic feeding system based on PCA［J］.Computer Engineering and Design，2012，33（12）：4746-4750.