高精度数控机床进给伺服系统的模糊自适应PID 控制

许文斌，曾全胜

(1.长沙航空职业技术学院，湖南长沙 410014;2.中南大学，湖南长沙 410083)

数控机床的进给伺服控制是一种误差控制，一般都采用传统PID 控制［1］。因结构简单、易于控制且无静态误差，PID 控制器被广泛应用于工业工程控制。然而，传统PID 控制器主要应用于具有确定模型的线性系统中。实际上，数控机床进给伺服系统的运行过程是复杂的，具有参数时变和模型不确定等特点。由于进给伺服系统建模的动力学模型不仅与系统摩擦特性有关，同时要考虑扰动转矩的因素，尤其是机械传动系统阻尼、惯性和刚度等参数的影响，以致传统的PID 控制很难得到较好的控制性能。

周磊等人［2］将超精密车床进给系统设计成为具有电流环、速度环和位置环的三环结构，并根据实际伺服特性，在位置环上设计了具有速度/加速度前馈补偿的半闭环复合控制策略。李军民等［3］基于标准遗传算法理论，提出了一种使交叉概率和变异概率随适应度值自动改变的自适应遗传PID 算法。S JEE 等［4］针对精密轮廓加工介绍了一种自适应模糊逻辑控制器(AFLC)，同时调整输入和输出的隶属函数。周若谷［5］建立了二输入三输出的单变量二维速度环自整定模糊控制器，获得了比普通PID 控制系统更好的控制性能。张礼兵等［6］针对高速高精度加工技术对数控位置伺服系统的控制性能提出的更高要求以及现行位置伺服控制方法存在不足的问题，提出了一种基于模糊推理的广义预测控制方法。柴光远等［7］针对数控进给伺服系统的特点及性能要求，应用免疫反馈系统的原理和模糊控制理论，在传统PID 控制基础上设计出一种模糊免疫自适应PID 控制器。

由于模糊控制具有鲁棒性强、对控制对象参数不敏感和超调量小的优点，文中提出了结合传统PID 控制的模糊自适应控制，并应用于数控机床的伺服控制系统。该控制器不仅具有模糊控制的灵活性和适应性，而且具有PID 控制的高精度，对于非线性、时变和随机控制对象，其控制参数能实时地自适应调整。

1 进给伺服系统的模型

数控机床通常是由数控系统、伺服系统、传动机构、工作台等部件组成。进给伺服系统一般包括伺服电机、滚珠丝杠、导轨、工作台和测量系统［8］，其功能是接收数控系统发来的控制命令，驱动工作台快速、平稳地移动。伺服驱动系统在工业领域扮演一个重要的角色，其性能的好坏对系统的运动精度产生极大的影响。测量系统包括位置、速度传感器，如光栅，脉冲编码器及其放大器电路，通过位置反馈、速度反馈，从而实现闭环控制。进给伺服系统X 轴示意图如图1 所示。

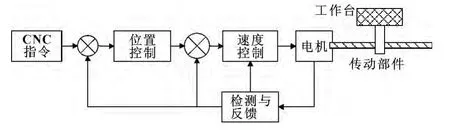
图1 进给伺服系统X 轴示意图

在进给伺服系统中，电机按照指令的顺序控制而转动，其角位移通过同高精度齿轮和精密丝杠螺母等机械传动装置转换成工作台的直线位移。进给伺服的机械传动和电气控制结构图如图2 所示［9］。由于系统具有大惯量、刚度、摩擦、阻尼、干扰等特点，显然通过传统的PID 控制参数整定的方法难以达到伺服系统的动态性能要求。

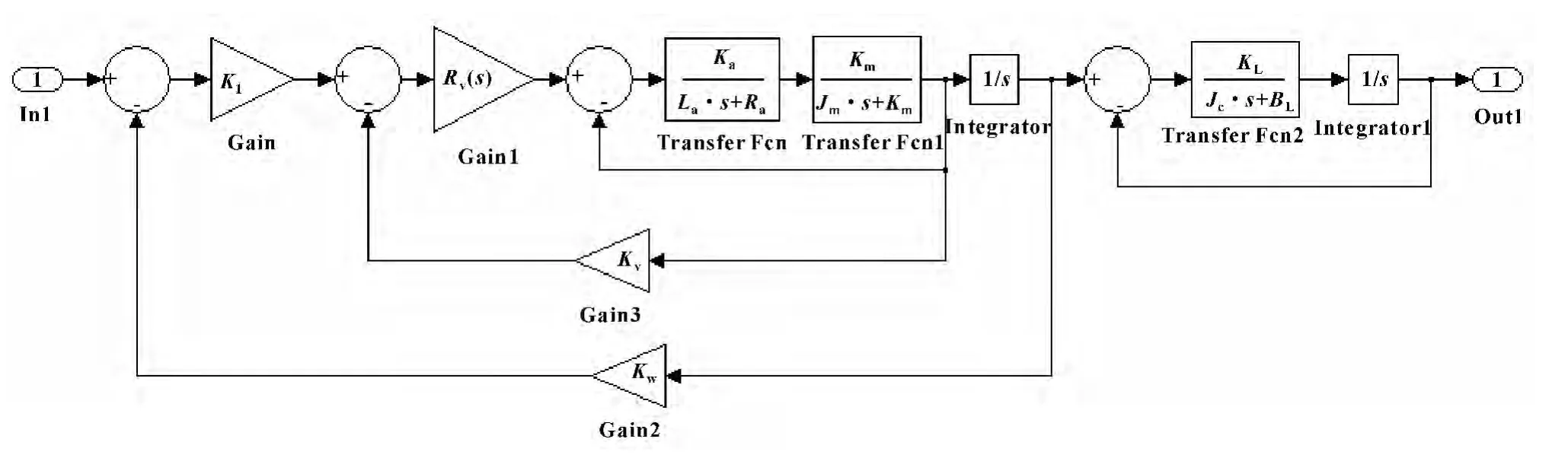
图2 进给伺服系统控制结构图

图2 显示，若全面考虑进给伺服系统各组成部件，则系统为一个五阶滞后系统，为了便于研究，可将伺服系统简化为一个二阶系统，如式(1)所示:

2 模糊PID 控制器的设计

模糊控制器根据人工控制规则，产生控制决策表，确定控制量，而无需被控对象的精确数学模型。图3 为模糊自适应PID 控制系统的结构图，可知系统由传统的PID 控制和模糊控制两部分组成。偏差e 和偏差变化率ec 为模糊控制的输入，输出为ΔKp、ΔKi、ΔKd，对于不同的e 和ec，PID 参数依据模糊控制规则进行自适应调整，以满足控制要求。

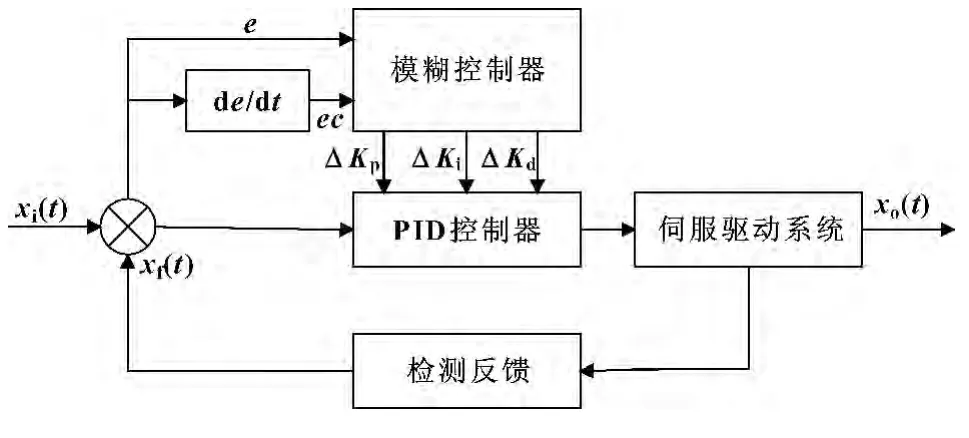
图3 伺服系统模糊自适应PID 控制结构图

PID 自整定参数按式(2)进行计算:

式中:Kp0、Ki0、Kd0为PID 参数的初始值，ΔKp、ΔKi、ΔKd为模糊控制的输出，Kp、Ki、Kd为最终控制输出参数值。

选择“mamdani”模糊控制器模型，输入和输出变量的隶属函数选择为三角形，论域设为［-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6］，语言变量设为{NB，NM，NS，O，PS，PM，PB}。

通常，PID 控制算式为:

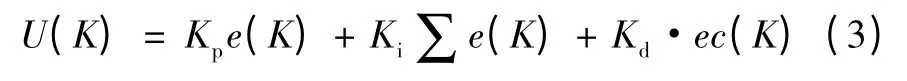
式中:e(K)为系统偏差，ec(K)为系统偏差变化率，Kp、Ki、Kd分别为控制器比例、积分、微分系数。

Kp的作用是加快系统响应速度，提高系统控制精度，当Kp较大时，系统响应速度快，但易出现超调，导致系统不稳定。Ki的作用是消除系统静态误差，Ki越大，系统的静态误差消除越快，但在响应初期会产生积分饱和现象，从而引起响应过程的较大超调。Kd的作用是改善系统的动态特性，主要是在响应过程中抑制偏差过大或过小，对偏差变化进行提前预报，但Kd过大会使响应过程提前制动，从而延长调节时间，降低系统的抗干扰性能［10］。

根据Kp、Ki、Kd对系统输出特性的影响，确定如下PID 自调整控制规则:

(1)当偏差e 较大时，为加快响应速度、尽快消除偏差，同时防止积分饱和，避免出现较大超调，Kp取较大值、Kd取较小值、Ki取零。

(2)当偏差中等大小时，既要继续减小系统偏差，又要防止产生超调，还要尽量缩短调整时间，此时Kp要适当减小、Kd取较小值、Ki适中。

(3)当偏差较小时，为了确保系统具有良好的稳态性能，同时响应过程出现震荡并提高系统抗干扰能力，应适当增加Kp、Ki，Kd取适中值。

Kp、Ki、Kd的模糊控制规则如图4 所示。

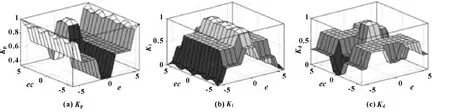
图4 Kp、Ki、Kd的模糊控制规则

3 仿真研究

以某数控机床X 轴进给伺服系统作为研究对象，取工作台质量m=1 500 kg，滚珠丝杠螺距h=5 mm，螺纹长度L=1.5 mm，螺杆轴向刚度KE=1.1 ×108N/m，螺杆的接触刚度KN=2.0 ×108N/m，电机转动惯量J=0.013 23 kg·m2。在以上给定参数的基础上构建系统机电耦合传递函数，基于MATLAB/Simulink 平台设计系统模糊自适应仿真原理图如图5 所示。

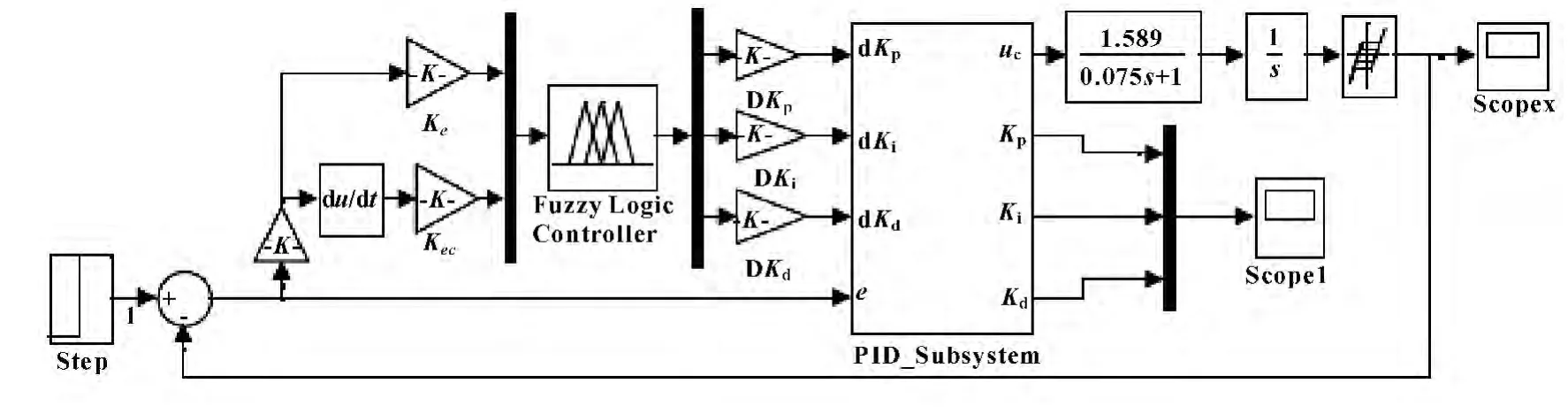
图5 系统模糊自适应仿真原理图

取PID 控制器初始值Kp0=30、Ki0=0.5、Kd0=15，仿真时间为4 s，以阶跃信号作为输入，Kp、Ki、Kd的调节过程如图6 所示。仿真结果表明:和传统的PID 控制器相比，模糊自适应PID 控制可以依据偏差e 和偏差变化率ec 对ΔKp、ΔKi、ΔKd三个参数进行在线修正，从而自动调整Kp、Ki、Kd，满足控制需求。

模糊自适应PID (F-PID)控制和传统PID (CPID)控制的阶跃响应与斜坡响应分别如图7 和图8所示。结果表明模糊自适应PID 控制系统具有超调小、精度高、稳定性好、较好的自适应性和强鲁棒性等较好的动态特性。

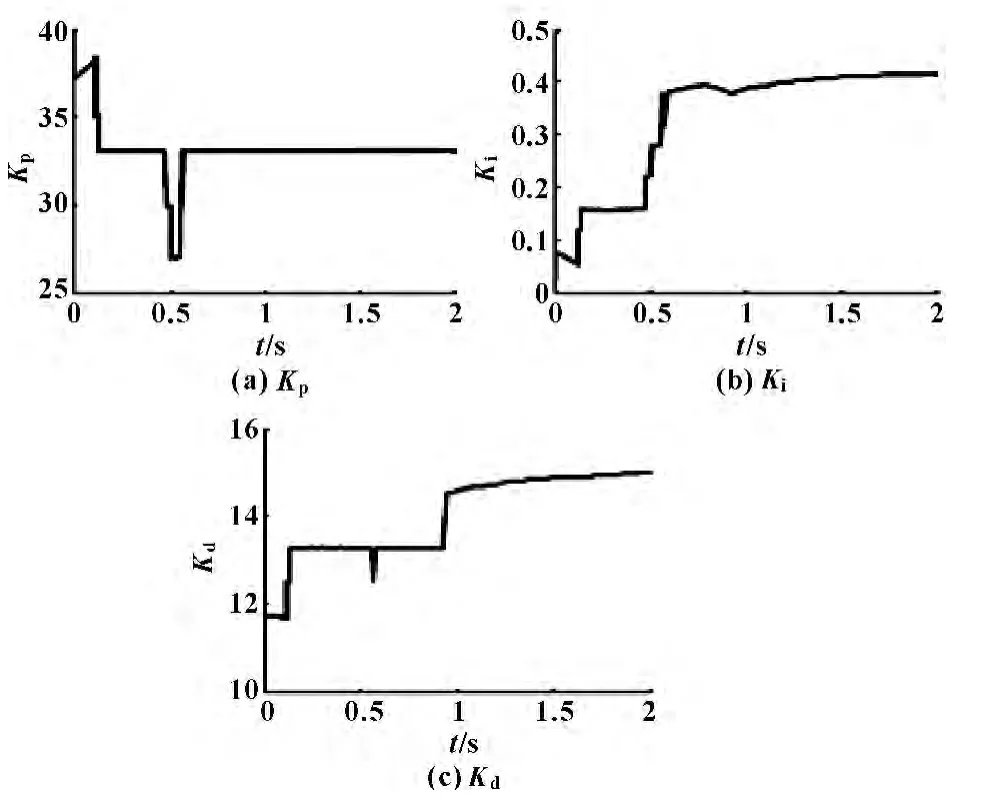
图6 模糊自适应PID 控制系统Kp、Ki、Kd变化曲线

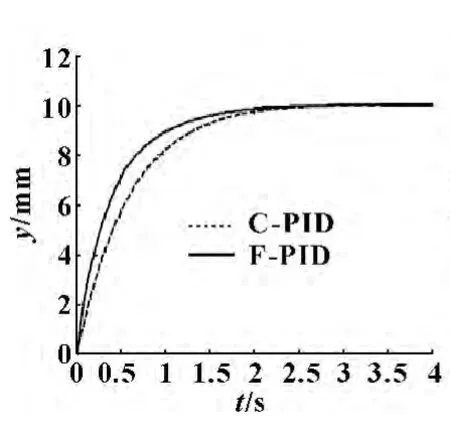
图7 C-PID 和F-PID阶跃响应比较

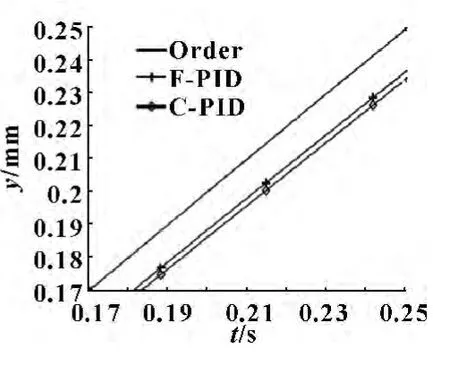
图8 C-PID 和F-PID斜坡响应比较

4 结论

本文提出了基于模糊PID 控制的进给伺服系统的控制理论，并将所设计的模糊PID 控制器应用于数控机床进给伺服系统的控制。该控制器可通过测量误差及误差变化率在线自整定PID 控制器的3 个参数。仿真结果表明，模糊PID 控制器的应用可以减少建模的困难，无需考虑系统的精确模型。和常规的PID 控制器比较，模糊自适应PID 控制器具有较强的鲁棒性、较快的响应速度和较高的控制精度。

［1］苏宏志.基于PID 控制的数控机床进给伺服系统的建模与仿真［J］.国内外机电一体化技术，2010(6):37－39.

［2］周磊，陈时锦，程凯.超精密车床进给伺服系统的复合控制设计［J］.机械设计与制造，2007(2):92－93.

［3］李军民，李虎.自适应遗传算法在数控伺服系统控制参数优化中的应用［J］.西北大学学报:自然科学版，2011(3):430－434.

［4］JEE S，KOREN Y.Adaptive Fuzzy Logic Controller for Feed Drives of a CNC Machine Tool［J］.Mechatronics，2004，14(3):299－326.

［5］周若谷.进给伺服系统模糊自整定控制建模与仿真［J］.武汉理工大学学报:信息与管理工程版，2011(1):47－50.

［6］张礼兵，游有鹏，吴婷.数控位置伺服系统控制策略研究［J］.中国机械工程，2012(14):1693－1697.

［7］柴光远，赵鹏兵.数控进给伺服系统的模糊免疫自适应PID 控制研究［J］.组合机床与自动化加工技术，2009(8):74－77.

［8］董玉红，邵俊鹏，周室仁.CK7815 数控机床进给伺服系统的建模及仿真［J］.哈尔滨理工大学学报，2005(3):25－27.

［9］张祺，侯力，蒋维旭，等.数控机床进给伺服系统模糊自适应PID 仿真［J］.机械设计与制造，2011(9):149－151.

［10］贺徽，周建中，谭建华，等.基于Mamdani 模糊PID 的同步发电机励磁控制［J］.华中科技大学学报:自然科学版，2010(2):34－37.