机夹式型线铣刀刀片槽检测技术研究
杨林建,刘淑香,徐化文,张金华
(1.四川工程职业技术学院,四川德阳 618000;2.东方汽轮机集团公司,四川德阳 618000)
1 刀体结构建模
2273-091092A 机夹式型线刀体为圆柱状旋转结构,其主要特点为每圆周四层节圆上均匀分布计48 个刀片槽,并且每层刀片槽相对上层刀片槽有22.5°的角度,因刀片槽数量多,尺寸小,每层刀片槽相对上层刀片槽有非90°角度,精度要求在±0.005 mm 以内,精度要求高,故增大检测难度。模型结构见图1。
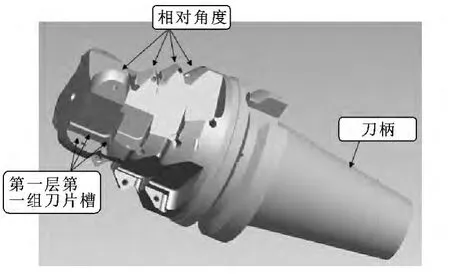
图1 2273 -091092A 机夹式型线刀体三维模型
2 数据要求
该刀体用于刀具研究人员进行数据分析,也用于实际生产,检测数据要求直观、易分析,工艺要求各刀片槽位置尺寸按±0.005 mm 控制。
面构成要素可用一线及一点方式,即测量出平面上一条线及一个点进行平面定位,此方法结果为线的质心点坐标、角度及平面所通过点的坐标值。因刀片槽平面很小,所检测出的角度误差很大,计算如下:arctan (0.01/3)≈10',当检测的实际值与理论值差0.01 mm 时,反映在面上的角度值就差10',该检测数据不能真实、直观反映出实际刀具与理论刀具差值,不利于数据分析及评价。
如采用三点确定面,即测量出面上3 个实际点,此方法的结果是面所通过3 个点的坐标值,也就是实际点与理论面距离,检测数据直观,方便刀具研究人员对检测数据进行分析。但点是平面元素,在测量中误差较大,误差分析及数据见图2 和表1。
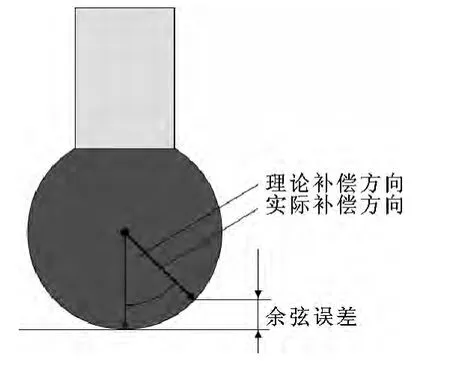
图2 点平面误差分析
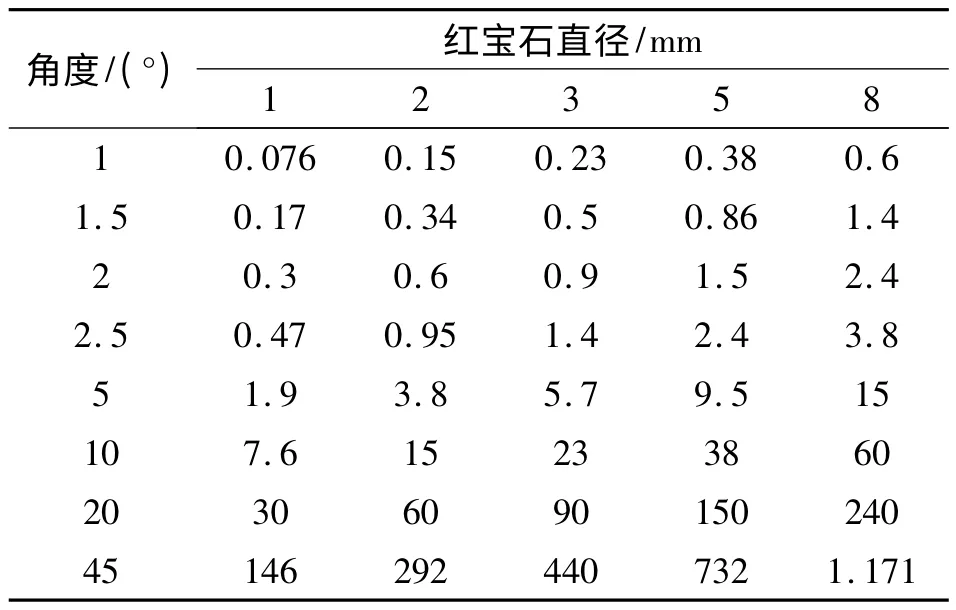
表1 误差分析表 μm
最终想要获得红宝石球与工件表面接触的特征点,两个点之间间距为触测方向(矢量方向)上的测针半径值,这需要通过测头补偿来实现,即将红宝石球心点沿测针触测方向补偿测针半径之后,得到工件表面的特征点。矢量在软件中重要作用是利用矢量方向进行测头半径补偿。当测量一点后,机器沿着与被测点矢量方向相反方向进行触测,测头补偿也是沿着同样方向。如果触测方向不正确,将引起“余弦误差”。
为方便刀具研究人员分析数据,检测元素为点,48 个刀片槽共144 个点,人为手动测量,工作量大,必须使用三维模型来实现自动化检测。但如在三维模型上读取理论点坐标来实现自动化,虽减轻了手动采点的劳动强度,但要在48 个面上读取144 个理论点,且每组理论值不一致,理论检测数据不直观,耗费的时间多,不利于刀具研究人员进行数据分析。
其次检测数据正负号不能代表工件实体高低,是在测量中长期以来存在的难题,因此不能很直观地判断面的高低,给科研人员进行数据分析带来了极大不便,坐标处理见图3。
图3 所示设点1 的理论坐标值Y1=+40 mm,实测值Y=+40.02 mm,偏差为0.02 mm。点1 实测值应越大越高,反之低。现实测值比理论值大,则证明实体高出理论,则偏差符号为正。
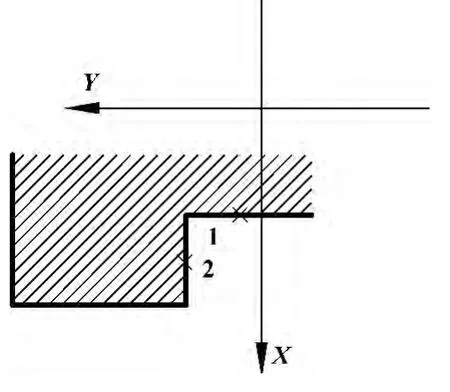
图3 坐标处理
图3 设点2 的理论值为Y2=20 mm,实测值为Y=19.99 mm,偏差为-0.01 mm。点2 实测值应越大越低,反之高。现实测值比理论值小,则证明实体高出理论,现偏差符号为-,要减少科研人员数据分析的时间,就必须使实体高低符号化。
由于程序中名称变量只允许在末尾,要满足高效的自动检测,只能将面的序号名作为变量,所以只能将面的序号放在名称末尾,而不能将点的序号作为变量。检测出的结果排列不直观是因为点的序列号在面的序列号之前,因此检测结果优先按点排列,故一个面上的3 点分布在不同的位置,并且每个平面上的点的理论数据不一致,且偏差结果不可靠,检测出来的数据只有通过刀具研究人员在Pro/E 模型上逐点输入后进行对比,如检测出现误差,则无法及时发现,且刀具在检测完成后,依然要占用仪器,直到数据分析完成后才可取下刀具进行其他工件的检测。如何解决数据排列及结果偏差的直观性是检测中的难点。
3 检测方案设计
3.1 仪器选择
刀体的诸多结构特点以及其较高的精度要求,同时为了保证高效率的检测,必须使用三维模型来实现自动化检测,因此,选择一台能够实现三维测量的高精度仪器进行该刀体的测量。2011年12 月引进一台海克斯康Reference600 三坐标测量仪,其主要性能体现在能够导入三维模型、精度高、检测过程依靠程序实现、可开发性强,在进行批量检测时效果尤为明显。
3.2 测针选用
针对刀体结构复杂,测量面小,只能选用直径尽可能小、测杆尽可能长的测针,并且要具备不同的方向,所以选用φ1.5 mm×30 mm 的测针。为避免测针干涉,选用水平4 个星型测针对刀体进行测量,如图4 所示。

图4 测针结构及安装
要避免测量时采点的误差,就需要使用三维模型自动采集,提取面的点来消除点的测头补偿误差;即要保证高效检测,又保证数据的可分析性,就必须让程序实现三维模型自动检测,且保证每一层的4 组刀片槽理论数据一致;要保证实体高低符号化,即必须提取实测面的矢量方向来计算实测值;为了检测数据直观、减少分析及结果评价时间,需要用程序实现检测数据按面的方式排列。
4 检测
4.1 探针校验
多数测量任务中,需要在不同坐标平面内进行不同性质测量,比如点、直线、平面、内/外圆柱面、距离、角度等。要完成这些任务,不但需要选用长度、直径、方位等参数和测针,还要求所选测针球心之间的相对位置关系,才可能使不同测针测出的几何元素具有正确的坐标关系。测针校准的目的就是确定各个测针的参数及它们相互间位置关系。探针校验如图5 所示。

图5 探针校验
4.2 确定检测基准及工件装夹
坐标测量机测量工件时,通常不需要对被测工件进行精确调整定位,根据软件功能建立工件坐标系,即柔性定位。为了能做到合理地建立工件坐标系,选择测量基准时应按使用基准、设计基准、加工基准的顺序来考虑。因加工时以刀具柄部圆锥面作为基准,故检测以柄部圆锥面作为第一检测基准;为了利于数据分析和结果判定,以第一周刀片槽最大的面作为第二基准,装夹时将刀片槽向左旋转5°~10°,以避免测针干涉。如图6 所示。
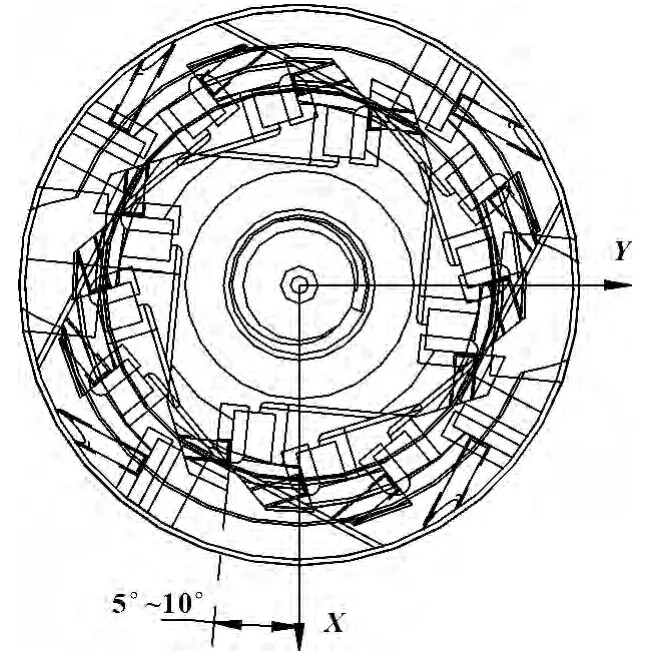
图6 工件装夹旋转示意图
该铣刀精度要求高,需要加入温度补偿,须设置并调用可靠的机器参数。因使用时以刀具柄部进行装夹定位,根据检测基准的选用原则,使用基准为首选,采用CadLoadModel 语句导入理论模型后,进行元素分组,粗建坐标系,手动在圆锥的一个截面上采集一个圆粗建坐标系确定X、Y,手动采集第一层第一个XZ 面作为第二基准确定Y 方向,采用GENCON程序自动计算出理论圆锥测量点及调取第二基准面和确定Z 轴高度进行自动测量,测量圆锥时先设置多方向测针的安全距离以防止干涉。自动测量完成后,精建坐标系,如图7 所示;机器坐标系与模型坐标系统一,如图8 所示。
图7 精建坐标系
图8 坐标系建立
为了后续自动写入评价偏差,避免手动评价,提高检测效率,坐标系建立完成后,将±0.02 分别赋值给UTL 及LTL。
采用循环语句DO、ENDDO 完成检测不同层及不同组的刀片槽。为了消除测头补偿误差,程序采用MEPLA 语句进行面的测量,避免重复测量,收集已采面的点,所测即为红宝石球与工件表面接触的特征点;为使实体高低符号化,提取点的矢量U、V、W,乘以实际值减去理论值的差,赋值给DEV 即可。检测过程如图9、10 所示。
图9 检测过程图(一)

图10 检测过程图(二)
3 结论
根据刀体结构,采用循环语句DO、ENDDO 语句完成不同面的测量;
采用指令CRSUBTYP 可以将公差、计算的实际值(符号)加到元素上,无需手动评价,提高了检测效率。
程序采用三维模型自动测量,因刀体结构的限制,为使测针测量时不发生干涉,以高效率完成检测,刀体第一层的测量与第四层的测量方法基本一致,而第二层的测量与第三层的测量方法基本一致,这样即完成了高效的检测,程序思路也较清晰。
以往的刀体检测主要采用其他三坐标完成,因仪器的局限性,48 个刀片槽上的144 个点必须人为进行采点测量,由于要消除测头半径补偿的误差,测量出来的结果必须进行处理,才能得到真实的检测结果,效率低下,检测一个刀体的时间至少为一天;而刀具研究人员对结果的评价必须在数模上逐点输入进行对比,其工作量极其繁琐,且容易出错,评价的时间至少一天。由于理论数据不直观,数据分析的时间无法估量,采用Leitz Reference 600 三坐标和三维模型编制程序实现自动检测,大大减少了劳动强度,其效率至少提高了10 倍以上,如果进行批量检测,效果提高更为明显。
[1]张梅,费业泰,盛立.三坐标测量机测端动态有效作用直径影响因素分析[J].中国机械工程,2010,21(9):1018 -1021.
[2]汪平平,费业泰,林慎旺.柔性三坐标测量臂的标定技术研究[J].西安交通大学学报,2006,40(3):284 -288.
[3]张永红,朱耀华,胡滨.基于数控加工机床的自由曲面测量新方法[J].矿山机械,2010(12):25 -27.
[4]XIONG Z H,LI Z X.Probe Radius Compensation of Workpiece Localization[J].Transactions of ASME,Journal of Manufacturing Science and Engineering,2003,125:100 -104.
[5]吕晓明,郑叔芳.在线三维几何量测量软件研究[J].南京航空航天大学学报,1995(3):326 -332.
[6]孙科,贾美薇,田怀文.三坐标测量机测头半径实用补偿算法[J].制造业自动化,2009(4):67 -68.
[7]刘勇,杨洪涛.三坐标测量机测头系统动态特性研究[J].工具技术,2008(5):75 -77.

