马尾松人工纯林不同器官含碳系数分析

郭文清， 徐清乾， 许忠坤， 郭文平

(1.湖南省林业科学院， 湖南 长沙 410004； 2.攸县黄丰桥国有林场， 湖南 攸县 412307)

马尾松人工纯林不同器官含碳系数分析

郭文清1， 徐清乾1， 许忠坤1， 郭文平2

(1.湖南省林业科学院， 湖南 长沙 410004； 2.攸县黄丰桥国有林场， 湖南 攸县 412307)

以湖南省马尾松纯林为对象，利用假设检验和回归分析方法，对马尾松林木各器官以及全林木含碳系数进行了回归检验分析。结果表明： 林木各器官的含碳系数在统计上大都存在显著差异，树干不同高度处干材的含碳系数从上到下总体上呈逐渐增大的趋势，不同粗细树根的含碳系数根茎到细根、粗根依次减小，根茎、细根、粗根两两之间并无显著差异；83株解析木地上部分的平均含碳系数为0.5066，28株解析木树根的含碳系数为0.4919，全林木生物量的平均含碳系数为0.5052；林木不同器官及全林木生物量的含碳系数与林木直径和树高没有相关性。

马尾松； 含碳系数； 生物量； 假设检验； 回归分析

森林的固碳释氧功能对缓解全球气候变暖发挥着重要作用，因此森林碳储量监测日益受到重视，而含碳系数是一项重要的基础计量指标[1]。由于不同树种之间的含碳系数相对来说变化不大，比较以往的研究结果，可知国内外的很多学者都选取了平均含碳系数0.5[2-5]，也有的选取平均含碳系数为0.45的[6-7]。在《土地利用、土地利用变化和林业优良做法指南》一文中，大力推荐使用0.5作为含碳系数[8]。但是，很多学者经过大量的研究证明，不同的树种它们的含碳系数是有区别的[9-14]。我们以湖南马尾松纯林的含碳系数测定数据，对各个器官含碳系数进行分析，既为马尾松的碳储量评估提供计量依据，也为规范有关含碳系数测定工作提供参考。

1 研究区概况

研究样地位于湖南省怀化市会同县，地处云贵高原东缘斜坡、雪峰山脉的西南，气候属亚热带湿润气候。年平均气温16.6℃，极端最高温和最低温分别为39.1℃和-8.5℃；年均降雨量为1304.2mm，年均相对湿度达83%。境内群山起伏，土层深厚肥沃，气候温和，无霜期长，雨量适中，植被繁茂，为发展林业生产提供了得天独厚的优越环境[15]。

2 研究方法

2.1数据获取

2010年—2012年，在会同县83块固定标准地附近选择了83株与固定标准地立地条件相近，与马尾松人工林林分平均直径Dg和平均高HD相接近(一般要求相差在±5%以下)且干形中等的林木作为平均标准木(解析木)。

将解析木的胸径和冠幅全部进行实测，通过破坏性抽样方法将样木伐倒，进而测量树高和冠干长度。采用抽样方法测定林木各器官干重，最后推导计算出树根的干重。地上与地下部分干重之和即为解析木全林木生物量，将解析木生物量乘以相应生长级的株数并累加起来作为林分生物量的估算值。

2.2数据分析

2.2.1 假设检验

(1) 独立数据的假设检验

独立样本是由用于对比的两套样本组成的，本文中我们假设它们来自相同的总体，即假设：H0∶μ1=μ2，最后依照下面的公式计算统计量t的值[1,16]：

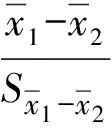
(1)

当n1=n2=n时，式(1)可以简化为：

(2)

依据样本的自由度df=n1+n2-2，查t分布的临界数值tα(一般取α=0.05)，最后把按照式(1)或式(2)计算得到的t的绝对值与tα的大小进行比较。假如大于tα，则否定假设H0；否则，假设成立，接受假设H0。

(2) 成对数据的假设检验

在对成对数据的平均数进行比较时，最先要假设2个样本所归属的总体平均数的差值是0，也就是假设H0∶μ1=μ2=0，把成对观测值之间的差值d=x1-x2当作一个新的变量，最后按照以下公式来计算统计量t值[1]：

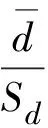
(3)

依据样本自由度df=n-1，查t分布的临界数值tα，最后把按照式(3)计算得到的t的绝对值与tα的大小进行比较。假如大于tα，则否定假设H0；否则，假设成立，接受假设H0。

2.2.2 回归分析 采用多元线性回归的方法对不同器官的含碳系数与林木的直径、树高以及年龄等因子之间是否存在相关进行分析。假设含碳系数与林木的直径和树高等因子满足以下线性回归方程：

y=a+bx1+cx2+ε

(4)

采取最小二乘法对参数进行估计。

(1) 回归方程的显著性检验

含碳系数的变化可以理解为由两部分组成：一是因为直径、树高和年龄发生了变化而引起的变化，这一部分可以利用回归方程式(4)来解释；另一部分是由其他的因素或者误差而产生的。运用n组观测数据对含碳系数进行回归估计分析，最后根据计算出的检验统计量F值与显著性概率P值进行分析[1]。

(2) 回归系数的显著性检验

回归方程式(4)假如在统计上是显著的，可以说明模型的回归系数b，c，d不全是0，但是不能排除其中一个或两个参数是0。如果某个系数值接近于0，说明它与0的显著差异性不大，就说明其相对应的变量对含碳系数的影响不显著。至于回归参数显著与否，要利用回归估计结果计算而来的检验统计量t与显著性概率P的值来进行分析判断[1]。

3 结果与分析

3.1树干不同高度处的含碳系数

分别在树干的7/1，3.5/10和1/10树高处(分别代表上、中、下三处)对干材取了2个样品测定其含碳系数，83株解析木共计504个测定数据。树干不同部位干材的平均含碳系数由上部到下部分别为0.4881，0.4996，0.5108。对上、中、下部(分别用1，2，3表示)干材含碳系数的差异显著性检验进行了分析，其t值结果如表1所示。

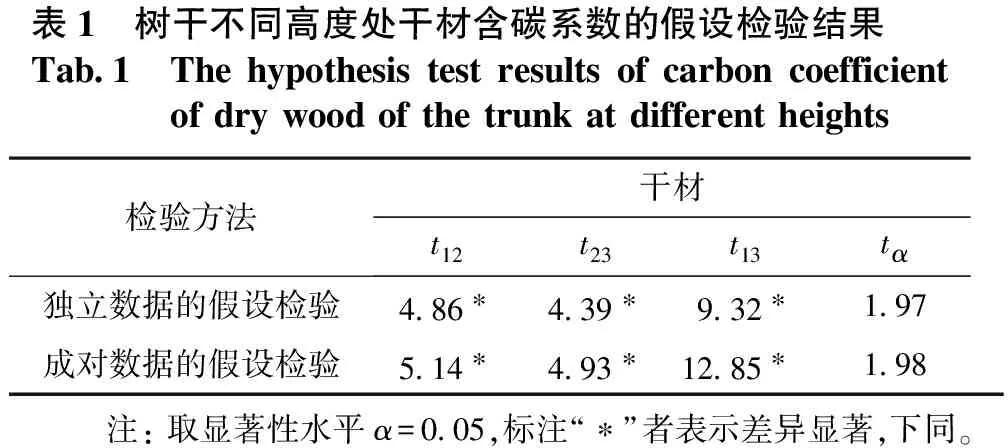
表1 树干不同高度处干材含碳系数的假设检验结果Tab 1 Thehypothesistestresultsofcarboncoefficientofdrywoodofthetrunkatdifferentheights检验方法干材t12t23t13tα独立数据的假设检验4 86∗4 39∗9 32∗1 97成对数据的假设检验5 14∗4 93∗12 85∗1 98 注：取显著性水平α=0 05，标注“∗”者表示差异显著，下同。

从表1可知，2种检验方法得到的结果一致： 树干上部和中部、上部和下部以及中部和下部的干材含碳系数差异均显著，上部和下部的差异检验值最大。其中，干材上部的含碳系数最小，下部最大。通过上、中、下3个部分的生物量进行加权计算得出干材处的平均含碳系数为0.5029。

3.2树根不同部位的含碳系数

在83株解析木中选取了28株测定地下部分的生物量和含碳系数，经过计算得到根茎、粗根(≥10 mm)和细根(2～10 mm，不含2 mm以下须根)处的平均含碳系数分别为0.4928，0.4891和0.4924。对树根不同部位(根茎、粗根、细根分别用1，2，3表示)的平均含碳系数进行了差异显著性检验，其t值计算结果见表2。

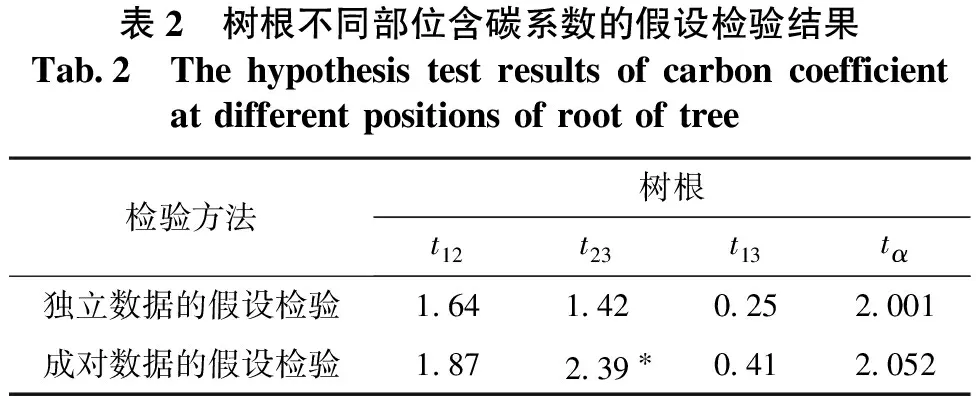
表2 树根不同部位含碳系数的假设检验结果Tab 2 Thehypothesistestresultsofcarboncoefficientatdifferentpositionsofrootoftree检验方法树根t12t23t13tα独立数据的假设检验1 641 420 252 001成对数据的假设检验1 872 39∗0 412 052

从表2可知，2种检验方法得到的结果稍有差异： 按照独立数据的假设检验结果可知，树根不同部位的含碳系数两两之间均无显著差异；而按照成对数据的假设检验结果可以看出，根茎和粗根的含碳系数之间无显著差异，根茎与细根的含碳系数之间也无显著差异，但是粗根和细根之间的含碳系数差异显著。由于在整个根系中细根的生物量所占的比例平均不足10%，又因为根茎与粗根的含碳系数之间并无显著差异，所以在现实林分中采样时可认为树根不同部位的含碳系数间无显著差异。树根含碳系数的算术平均值为0.4919。

3.3不同器官含碳系数的差异分析

根据83株解析木的含碳系数的计算结果，干皮、树枝、树叶含碳系数的算术平均值分别为0.4523，0.4828和0.5959。根据上述研究结果，全林木各器官的含碳系数从大到小的顺序依次为： 树叶>干材>树根>树枝>树皮，各器官含碳系数的平均值分别为： 0.5959，0.5029，0.4919，0.4828和0.4523。将地上部分各器官(包括干材、干皮、树枝、树叶，分别用1，2，3，4表示)的平均含碳系数进行差异显著性检验，其t值计算结果如表3所示。

表3 地上部分各器官含碳系数的假设检验结果Tab 3 Thehypothesistestresultsofcarboncoefficientofdifferentorgansaboveground检验方法地上部分t12t13t14t23t24t34tα独立数据的假设检验7 97∗3 47∗8 91∗3 56∗12 69∗10 47∗1 97成对数据的假设检验9 38∗4 12∗9 23∗4 26∗15 38∗12 61∗1 98

由表3可知，2种检验方法得到的检验结果一致： 干材、干皮、树枝、树叶两两之间含碳系数差异均显著。其中，干皮和树叶、树枝和树叶之间的差异相对较大。

根据干材、干皮、树枝和树叶各分项生物量及其含碳系数，可以加权算出每株解析木地上部分的含碳系数，83株解析木地上部分的平均含碳系数为0.5066。该值介于树叶和干材的含碳系数之间，很明显与树根的含碳系数有显著差异。树叶含碳系数0.5959和树皮含碳系数0.4523与树根含碳系数0.4919有显著差异，而树根含碳系数与干材、树枝和地上部分含碳系数的差异通过利用式(1)进行计算，其t值分别为3.59，2.67和1.86，与临界值1.97相比较，说明树根含碳系数与树枝、干材含碳系数均有显著差异，与地上部分差异不显著。根据地上部分和地下部分生物量及其含碳系数，可以加权算出每株解析木全林木的含碳系数，28株解析木的平均含碳系数为0.5052。不同器官及全林木含碳系数之间的对比情况见图1。

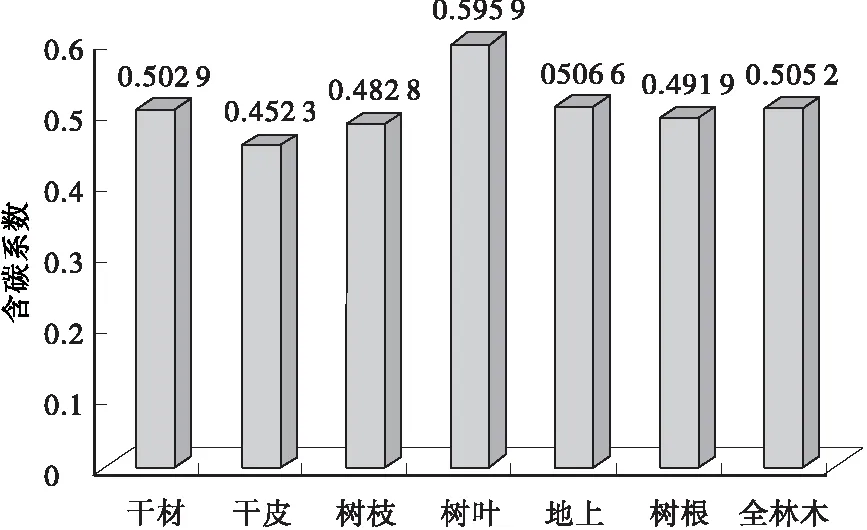
图1 不同器官含碳系数对比Fig.1 The contrast of carbon coefficient of different organs

3.4不同器官含碳系数的相关分析

根据上述研究基础，建立干材、干皮、树枝、树叶、地上部分、地下部分(树根)及全林木含碳系数与林木直径和树高的线性回归方程(4)，将回归方程显著性指标F值、P值以及回归系数显著性指标t值和p值的计算结果列于表4。

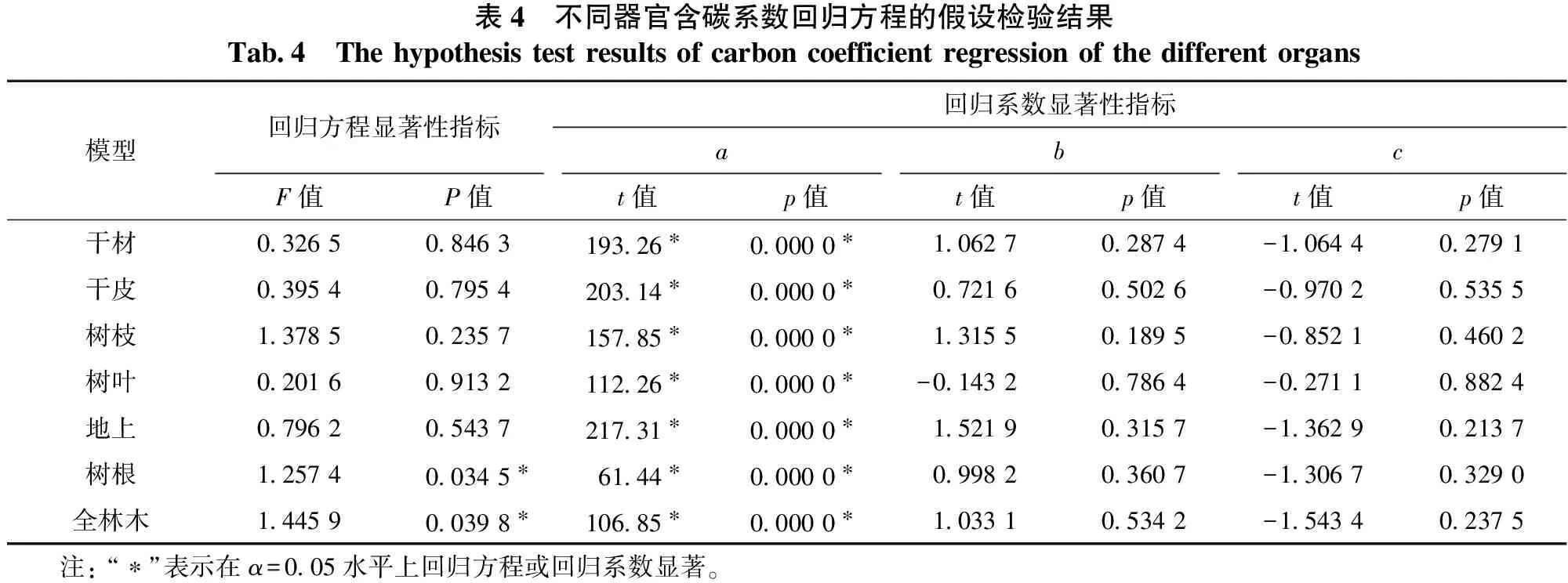
表4 不同器官含碳系数回归方程的假设检验结果Tab 4 Thehypothesistestresultsofcarboncoefficientregressionofthedifferentorgans模型回归方程显著性指标回归系数显著性指标abcF值P值t值p值t值p值t值p值干材0 32650 8463193 26∗0 0000∗1 06270 2874-1 06440 2791干皮0 39540 7954203 14∗0 0000∗0 72160 5026-0 97020 5355树枝1 37850 2357157 85∗0 0000∗1 31550 1895-0 85210 4602树叶0 20160 9132112 26∗0 0000∗-0 14320 7864-0 27110 8824地上0 79620 5437217 31∗0 0000∗1 52190 3157-1 36290 2137树根1 25740 0345∗61 44∗0 0000∗0 99820 3607-1 30670 3290全林木1 44590 0398∗106 85∗0 0000∗1 03310 5342-1 54340 2375 注：“∗”表示在α=0 05水平上回归方程或回归系数显著。

从表4可知，7个回归方程均不显著，即各个自变量的回归系数在统计上与0均无显著差异；从回归系数的显著性检验来看，除了全部的常数项a均极其显著以外，其余系数均不显著。说明各器官的含碳系数相对稳定，林木直径和树高的大小对各器官的含碳系数均没有影响，各器官含碳系数不随林木直径和树高的变化而变化。研究结果与曾伟生[17]、党永峰[18]等学者的研究结果相对一致。

4 结论与讨论

通过对马尾松纯林林木各器官含碳系数的分析可知，林木各器官的含碳系数在统计上大部分都有着显著差异，按从大到小的顺序依次为：树叶>干材>树根>树枝>树皮，其平均含碳系数分别为： 0.5959，0.5029，0.4919，0.4828和0.4523。树干不同位置处干材的含碳系数总体上表现出从上到下逐渐增大的趋势，上部的含碳系数明显小于中部和下部，而中部的含碳系数小于下部的含碳系数，其中上部和下部的含碳系数差异最显著；树根不同部位的含碳系数有从根茎到细根、粗根依次减小的趋势，根茎、细根、粗根两两之间并无显著差异；林木地上部分和地下部分的含碳系数没有显著差异，83株解析木地上部分的平均含碳系数为0.5066，28株解析木树根的含碳系数为0.4919，全林木生物量的平均含碳系数为0.5052；林木各个器官以及全林木生物量的含碳系数在一定的范围内比较稳定，与林木的直径以及树高的大小并无关系。

基于以上分析，林木各器官的含碳系数应该分别测定，其中在树干处还需要分别测定其上、中、下3部分。

[1] 高惠璇.实用统计方法与SAS系统[M].北京：北京大学出版社，2001.

[2] 李永慈，唐守正，李海奎.用两阶段度量误差模型方法和ForStat软件进行模型整合[J].林业科学，2004，2(40)：75-78.

[3] Fang J，Chen a P，Peng C H，et al. Changes in forest biomass carbon storage in China between 1949 and 1998[J].Science，2001(292)：2320-2322.

[4] 刘国华，傅伯杰，方精云.中国森林碳动态及其对全球碳平衡的贡献[J].生态学报，2000，20(5)：733-740.

[5] 方精云.中国森林生产力及其对全球气候变化的响应[J].植物生态学报，2000，24(5)：513-517.

[6] 马钦彦，谢征鸣.中国油松林碳储量基本估计[J].北京林业大学学报，1996，18(3)：23-27.

[7] Malhi Y,Baldocchi D D, Jarvis P G. The carbon balance of tropical，temperate and boreal forests. Plant [J].Cell and Environment，1999(22)：715-740.

[8] 周玉荣, 于振良, 赵士洞.我国主要森林生态系统碳贮量和碳平衡[J].植物生态学报，2000，24(5)：518-522.

[9] IPCC. Good Practice Guidance for Land Use Change and Forestry[M].Japan：the Institute for Global Environmental Strategies for the IPCC，2003.

[10] 马钦彦，陈遐林，王娟，等.华北主要森林类型建群种的含碳率分析[J].北京林业大学学报，2002，24(5/6)：96-100.

[11] 唐宵，黄从德，张健，等.四川主要针叶树种含碳率测定分析[J].四川林业科技，2007，28(2)：20-23.

[12] 罗云建，张小全，候振宏，等.我国落叶松林生物量碳计量参数的初步研究[J].植物生态学报，2007，31(6)：1111-1118.

[13] 顾凯平，张坤，张丽霞.森林碳汇计量方法的研究[J].南京林业大学学报：自然科学版，2008，32(5)：105-109.

[14] 康冰，刘世荣，蔡道雄，等.南亚热带杉木生态系统生物量和碳素积累及其空间分布特征[J].林业科学，2009，45(8)：147-153.

[15] 张华英.基于3S技术的农林复合生态系统景观格局分析——以湖南省会同县为例[D].长沙：中南林业科技大学，2003.

[16] 胡建颖，冯泰.实用统计学[M].北京：北京大学出版社，2002.

[17] 曾伟生，肖前辉.南方马尾松不同器官的含碳系数分析[J].中南林业调查规划，2011，30(2)：51-55.

[18] 党永峰，曾伟生，王雪军. 东北落叶松不同器官的含碳系数分析[J].林业资源管理, 2011(4)：31-34.

(文字编校：张 珉)

AnalysisoncarboncontentfactorsofdifferentorgansofpurePinusmassonianaforest

GUO Wenqing1, XU Qingqian1, XU Zhongkun1, GUO Wenping2

(1.Hunan Academy of Forestry，Changsha 410004， China; 2.Huangfengqiao Forestry Farm of Youxian, Youxian 412307, China)

Based on the data of purePinusmassonianaforest in Hunan province, the carbon content factor (CCF) of different organs and the whole tree were analyzed using hypothesis test and regression analysis. The results showed that, in statistics the CCF of different organs were almost significantly different, stem wood’s CCF increased from the top to the down.The order by CCF of different thickness roots from highest to the smallest was rhizome, thin root and thick root, there was no significant difference among them.The average CCF of the 83 parse trees was 0.5066, root’s average CCF of 28 parse trees was 0.4919, average CCF of whole tree’s biomass was 0.5052.The CCF of different organs and whole tree’s biomass were not related to its diameter and height.

Pinusmassoniana; carbon content factor; biomass; hypothesis test; regression analysis

2014-04-24

湖南省林业科技项目“湖南近自然森林经营试验与示范”(2012-HNLYKY-03)。

郭文清(1987-)，男，河南省林州市人，硕士，主要从事森林经理和马尾松经营技术研究。

S 791.248

A

1003-5710(2014)04-0040-05

10. 3969/j. issn. 1003-5710. 2014. 04. 009