全球重力场模型EGM2008精度分析与改进研究

■陈秋阳，陈尚云

■1.中国水电顾问集团中南勘测设计研究院有限公司，湖南 长沙 410014;2.四川中水成勘院测绘工程有限责任公司，四川 成都 610072

1 前言

随着美国全球定位系统(GPS)、俄罗斯全球卫星导航系统、中国北斗卫星导航系统(BDS)、和欧盟卫星导航定位系统(GALILEO)的不断完善和投入民用，GNSS测量的可靠性和精度逐步提高，其应用范围也越来越广。

由于GNSS测量得到的成果是WGS84坐标系的地心坐标(X，Y，Z)或大地坐标(B，L，H)，而用户需要的成果则是参心坐标(如1954北京坐标或1980西安坐标)和正常高，因此，需要将大地坐标(B、L、H)转换为参心坐标(x、y)和正常高h。平面坐标转换相对容易实现，而将大地高H转换为正常高h则需要确定精确的高程异常ζ(即h=H－ζ)，由于似大地水准面的不规则性，大地高H转换为正常高h的精度较低。为提高GPS大地高H的利用效率，近来由NGA(US National Geospatial－IntelligenceAgency)推出的全球超高阶地球重力场模型EGM2008以确定全球似大地水准面，该模型的阶次为2159(另外球谐系数的阶扩展至2190次)，相当于模型的空间分辨率约为5＇(约9 km)。该模型采用了GRACE卫星跟踪数据(ITG－GRACE03S位系数信息以及相应的协方差信息)、卫星测高数据和地面重力数据等，该模型无论在精度还是在分辨率方面均取得了巨大进步，采用该模型以及GPS水准数据有望获得更高精度的区域似大地水准面。

下面我们以工程实例对全球重力模型EGM2008的精度进行分析，并提出精度改进方法。

2 EGM2008模型精度分析

2.1 工程1分析

工程1施测了16个控制点，控制面积约80km2，控制点分布见图2－1，各点大地坐标与正常高值见表2－1。

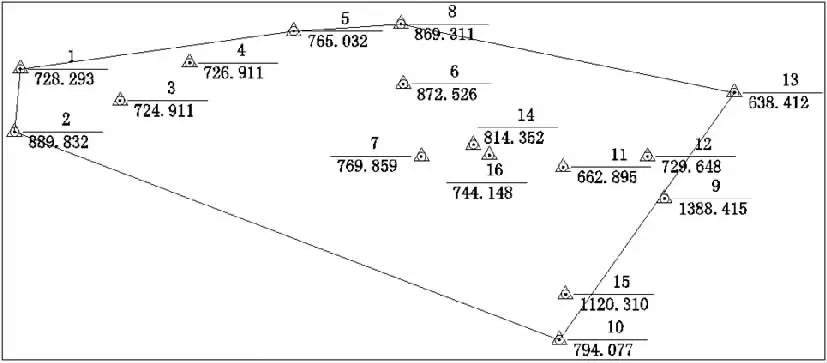
图2 －1

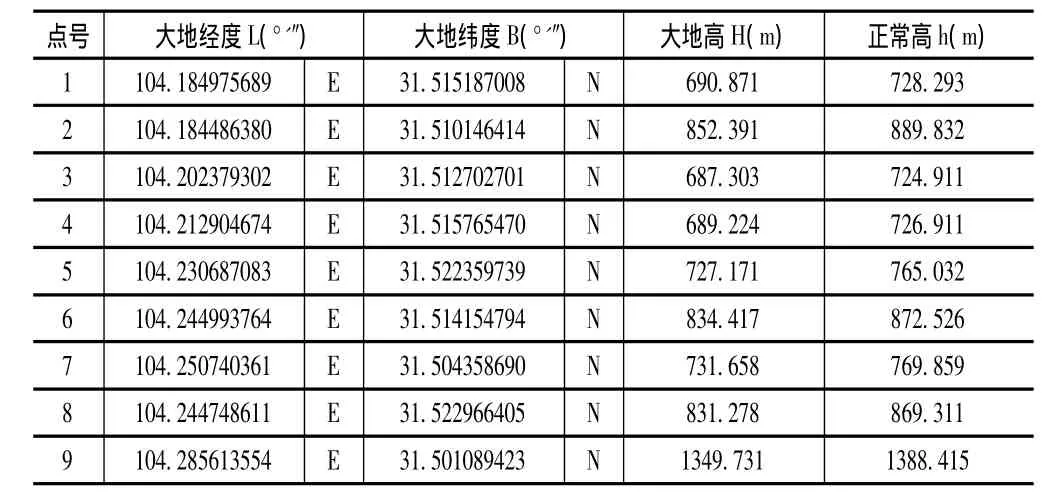
表2 －1 GPS控制点大地坐标与正常高值

点号 大地经度L(°＇″) 大地纬度B(°＇″) 大地高H(m) 正常高h(m)10 104.271805332 E 31.481736606 N 755.431 794.077 11 104.272082132 E 31.503576736 N 624.410 662.895 12 104.283992279 E 31.504462179 N 691.031 729.648 13 104.300153986 E 31.513604053 N 599.711 638.412 14 104.255647407 E 31.505334368 N 776.048 814.352 15 104.272371667 E 31.485384672 N 1081.706 1120.310 16 104.261130931 E 31.504508640 N 705.801 744.148

利用EGM2008模型计算表2－1中各点高程异常值，然后求得其正常高值，并与实测值进行比较，比较结果见表2－2。

表2 －2 GPS点EGM2008高程异常和计算高程成果表

表2－2中，第5列为EGM2008模型计算的正常高HEGM2008=大地高h－高程异常ζEGM2008;第6列为HEGM2008与实测正常高的较差△H=HEGM2008－h，最大值为0.437m，最小值为0.374m，中误差为±0.411m;然后采用常数拟合的方式，取较差均值对HEGM2008进行改正，得到改正后的模型正常高(见第7列);第8列为改正后的正常高与实测正常高的差值，最大值为0.032m，最小值为－0.031m，中误差为±0.018m。

2.2 工程2分析

工程2施测了21个控制点，控制面积约247290km2，控制点分布见图2－2，各点成果见表2－3。

表2 －3 GPS控制点大地坐标与正常高值

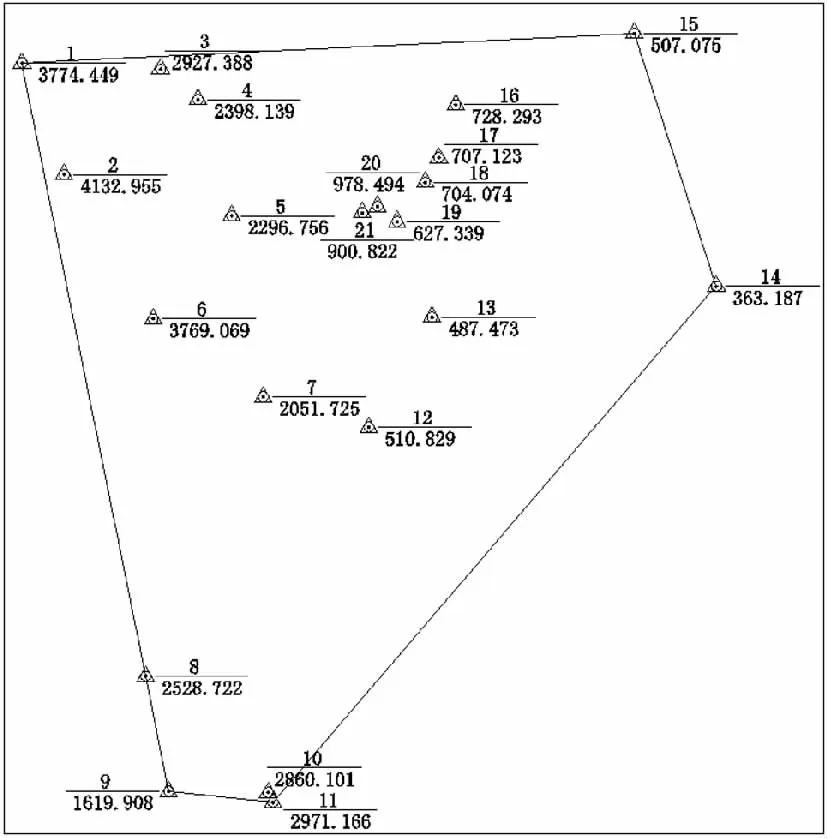
图2 －2

利用EGM2008模型计算表2－3中各点高程异常值，然后求得其正常高值，并与实测值进行比较，比较结果见表2－4。

表2 －4 GPS点EGM2008高程异常和计算高程成果表

根据工程1的计算方法，直接利用EGM2008模型计算的正常高与实测正常高间的较差最大值为2.189吗，最小值为0.041m，中误差为±1.067m;若利用较差均值进行修正，则较差最大值为1.074m，最小值为－1.074m，中误差为 ±0.671m，与工程 1相比，该工程区利用EGM2008获得正常高精度较低。

3 EGM2008模型正常高精度改进

从上述精度分析中可以看出，若直接利用EGM2008计算高程异常获取正常高值，其精度较低，如工程1为±0.411m，工程2为±1.067m;若利用较差均值对高程异常进行修正，则得到的正常高精度将得到很大的改善，经改正后工程1的精度为±0.018m，工程2为±0.671m;但工程2经均值修正后精度依然偏低。

为获取更优的正常高值，针对工程2，利用EGM2008模型正常高和实测正常高，对其差值按10参数多项式模型进行差值拟合，然后对EGM2008模型正常高值进行修正，表3－1是针对工程2进行的拟合计算。

表3 －1 EGM2008正常高优化计算

表3－1是利用21个控制点按10参数多项式拟合计算得到的模型和精度统计，该模型的内符合精度为±0.125m，最弱点正常高较差为0.318m;外符合精度为±0.168m。

若直接利用实测的大地高和正常高按10参数多项式模型进行高程异常拟合，模型成果和精度统计见表3－2。

点名 X(m) Y(m) h(m) H(m) 差值(m)1 3562523.880 208689.936 3742.081 3774.449 －32.368至21 3435605.135 496955.486 865.224 900.822 －35.598

利用该法，由21个点按10参数多项式模型拟合获取的正常高内符合精度为±1.212m，最弱点正常高较差为2.229m;外符合精度为±1.352，最弱点正常高较差为2.410m。

从上分析可知，利用EGM2008模型获取的正常高精度比直接利用GPS水准点进行模型拟合获取的正常高精度高;若利用残差对EGM2008模型正常高进一步改正，则获取的正常高精度更高。

4 结束语

本文利用工程实例分析了EGMM2008全球重力场模型的精度，并提出了改进EGM2008模型正常高精度的方法，所形成的工作经验表现在:

(1)当测区范围不大于20km×20km，且有一个已知高程点时，则根据已知点的EGM2008正常高与实测正常高的差值，对EGM模型正常高进行修正，可大幅提高EGM2008模型正常高精度，如工程1从±0.411m提高至±0.018m;

(2)当范围大到500km×500km时或EGM2008模型正常高精度较低时，可根据均匀分布于测区的控制点的EGM2008正常高和实测正常高的差值，采用多项式模型进行拟合，然后对EGM2008正常高进行修正，可大幅提高EGM2008模型正常高的精度，如工程2从±0.671m提高至±0.168m;

(3)根据工程实践经验，当测区范围不大于500km×500km、且有均匀分布的控制点时，可不再作图根水准测量或图根三角高程测量，可大大减少外业工作，从而提高经济效益。

［1］孔祥元，郭际明.刘宗全编著《大地测量学基础》武汉大学出版社，2005(12).

［2］於宗俦，鲁林成.《测量平差基础》(增订本)，测绘出版社，1983(6).