基于像素点聚类分离的滤波算法

刘 新，葛洪伟，张妨妨

江南大学 物联网工程学院，江苏 无锡214122

图像在生成和传输过程中容易产生脉冲噪声，如果图像中存在大量的脉冲噪声，将会直接影响图像分割、模糊处理、图像增强、图像分类以及图像的特征提取等处理，因此图像降噪是图像处理中必不可少的阶段。

对于图像降噪来说，难点在于如何在去除噪声的同时尽可能多地保护图像边缘和细节部分。经过不断努力，科研工作者已研究出很多优秀的基于中值滤波的相关算法，如开关中值滤波[1]，该算法利用滤波窗口中心像素点值与窗口中值之间的差值大小，通过与设定的阈值进行比较来判断噪声点；文献[2]提出了基于统计噪声检测的中值滤波，该算法考虑到滤波窗口中的噪声点数不止一个，又结合像素点之间的相似性，所以先求出除滤波窗口中心像素点之外的其他几个像素点与中心像素点之间的差值，再选择最小的四个差值进行统计计算，最后确定出噪声点并对噪声点进行滤除；文献[3-4]提出了基于极值噪声检测的中值滤波，该算法主要根据噪声点的孤立性和正常像素点之间的相似性，认为噪声点的像素值在滤波窗口中表现为极值，所以将处于极值状态下的窗口中心像素点判定为噪声点；文献[5]则是基于排序法的中值滤波，该算法将滤波窗口中的像素点按像素值大小进行升序排列，如果排序后窗口中心像素点的序号与窗口中值的序号相差比较大，则判断为噪声点。该算法对于边缘部分存在噪声点的漏检和误检。上述这些算法虽然能检测出噪声点并取得良好的滤波效果，但是还不能准确地检测出非明显噪声点，对于图像细节和边缘部分的保护方面依然不足，进而研究出基于图像像素点相似性的自适应中值滤波[6]、基于模糊分类的中心权值滤波[7-8]等新型滤波方法。文献[6-8]中的算法，都利用了正常像素点之间的相似性和噪声点的孤立性，文献[6]在滤波时根据污染程度的大小选择不同的滤波窗口，文献[7-8]根据待处理的像素点与阈值之间的差值进行中心权值估算，最后进行加权滤波；这两种算法较好地保护了图像的细节和边缘部分，但是还不能很好地检测出边缘部分的非明显噪声。

本文提出一种运用模糊C 均值聚类算法对图像进行噪声分离的滤波方法。首先对噪声图像进行初步滤波，并将滤波后的图像转换为相关矩阵，然后运用聚类算法进行自动分离，最后对分离出来的噪声点进行中值滤波。实验表明，对于不同的低污染度图像，文中的算法比上述文献中提到的滤波方法更能滤除噪声，同时保护更多的图像细节。

1 对图像的初步滤波

设待处理图像I 的尺寸为r×c，在I 中选择以xi，j为中心像素点的大小为(2L+1)×(2L+1)的滑动滤波窗口P，P={xi-L，j-L,xi-L，j-L+1,…，xi，j,…，xi+L-1,j+L,xi+L,j+L}，L ≤i ≤r-L-1，L ≤j ≤c-L-1。其中初步滤波的计算如式（1）：

2 图像相关矩阵的计算和转换

经过上述处理后得到新的噪声图像I′，原噪声图像I 中比较明显的噪声点已被滤除，但还是有很多不明显的噪声点存在，因此需要对图像I′进行如下处理。

2.1 图像像素值增强

不明显的噪声点在像素值上与正常像素点比较接近，为了区别出这类噪声点，进行像素值增强，以加大噪声点和正常像素点之间的差异。对于图像的平滑区域，滤波窗口内像素点的像素值都很接近，选择任何方向对像素点进行增强后，和原像素点的像素值基本相似；对于图像的边缘区域，如果沿着边缘方向进行像素值增强，将不会造成像素值过大的变化，反之，像素值将变化很大，最终被误判为噪声。对于图像中的噪声点来说，因为噪声点本身的孤立性，在任何方向上进行像素值增强后都会增加或者减少其像素值。因此，引入图1 中的四个方向算 子（zε为3×3 大 小 的 矩阵），对图像进行像素值增强。

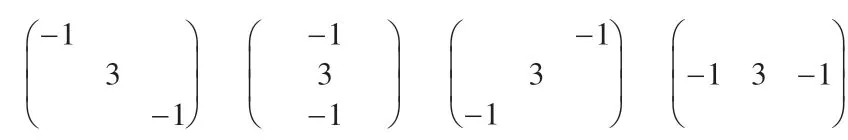
图1 用于像素值增强的四个方向算子

用图1中的四个方向算子分别与滑动窗口p′如式（2）进行计算，p′中取L=1，则滑动窗口p′的矩阵形式可以如图2进行表示；Tr(.)表示求矩阵(p′×zε)对角线上元素之和。最后选择四个值中最小的作为增强后的像素值：

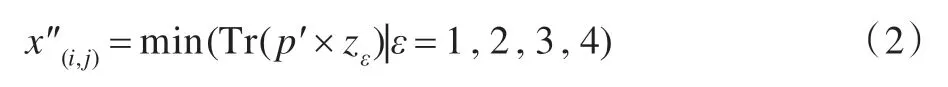
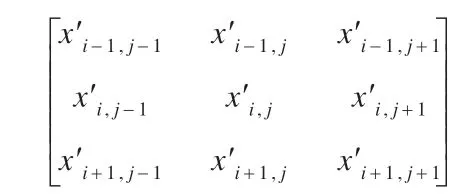
图2 滑动窗口p′的矩阵形式

2.2 图像相关矩阵计算

对于灰度图像来说，任意的滤波窗口中，无论是边缘区域还是平滑区域，如果待测像素点是正常像素点，那么都有大量像素点在像素值上与它相似。以3×3 的滤波窗口为例，如果中心像素点为正常像素点，那么有四个像素点与之在像素值上较接近[9]，这四个点代表了图像边缘的方向等信息。假设此时的滤波窗口为p″={x″i-L,j-L,x″i-L,j-L+1,…，x″i,j,…，x″i+L-1,j+L,x″i+L,j+L}，L=1，x″i,j为窗口中心像素点。相关矩阵的具体计算步骤如下：

（1）求取窗口p″中除中心像素点外的其他像素点与中心像素点x″i,j在像素值上的差值，并取差值的绝对值。计算公式如式（3）：

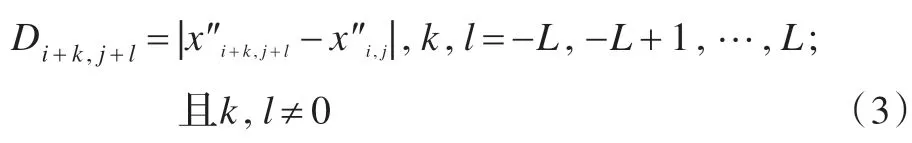
由此可得集合M，M 中共有(2L+1)2-1 个元素。

（2）从集合M 中选出最小的四个元素，分别标记为D1，D2，D3，D4，并进行式（4）计算得到元素ai，j：

2.3 相关矩阵的转换

经过上述步骤（1）和步骤（2）计算后得到ai，j(L ≤i ≤r-L-1，L ≤j ≤c-L-1)，由此得到相关矩阵A。为了便于下面的聚类处理，需要再次对相关矩阵A 进行转换，将正常像素点和噪声点分离开，因此对A 中的元素ai，j做如下处理得到bi，j，如式（5）：

其中q=25，p=4，int8 表示将数值范围缩小到0~255之间，并且取整数，即大于255 的数值为255，小于0 的数值为0。通过上述计算得到矩阵B，B 由元素bi，j(L ≤i ≤r-L-1，L ≤j ≤c-L-1)构成，通过计算后可得bi，j的值在25 到255 之间，并且正常像素点和噪声点的像素值分别向25 和255 靠近。

3 相关矩阵的模糊C 均值聚类

对于矩阵B 来说，如果简单地设置阈值T 进行阈值分割，可以区别出大部分噪声，但是对于不同图像来说，最佳阈值并不完全相同，此外，相关矩阵中噪声点和部分正常的边缘像素点较接近，阈值不可能精确地进行分离，因此会产生误判。为了避免上述两种情况，引入了模糊C 均值聚类[10-12]对相关矩阵进行自动分割，实验证明，该方法能取得良好的效果。对相关矩阵进行模糊C 均值聚类的具体步骤如下：

（1）模糊C 均值聚类的目标函数：

确定初始聚类中心后，进行S 次迭代，当JS-JS-1＜T时结束聚类，T 为聚类的判断精度，在本文中设置为0.000 01，S 的最大值设置为200。

（2）筛选聚类后的噪声类

在相关矩阵B 中转换后的噪声点的值都比较大，通过聚类分离后对矩阵B 进行标记，求取每类的平均值，平均值较大的这类点代表的则是图像中的噪声点，并对这类点进行中值滤波，滤波窗口大小为3×3，其他的点则被视为正常像素点保留下来。

4 实验结果及分析

（1）主观视觉比较

测试图的原图为512×512，256 灰度级的标准样本图像，测试图则分别在原图中添加了5%到20%的随机值脉冲噪声，本文进行了大量的实验，这里仅选出line、pepper 和boat 三幅测试图，将本文算法与SMF（标准的3×3 中值滤波）、ROAD-T[2]、MSWM[5]、CAFSM[7]几种算法进行比较。测试图像的原图如图3 所示；图4 至图6中（a）均为加入噪声后的图像，其中（b）~（f）分别表示不同滤波算法的滤波效果图。经过多次实验后，将本文实验参数设置为L=1，m=1.75，μ=40，T=0.000 01。由这些实验效果图可以看出本文算法比其他算法得到的滤波效果更好，尤其是在图4 中上端最细的那条白线在本文算法中保留得更完整。

图3 line、pepper和boat原图

图4 不同滤波算法对污染度为0.1 的line图的处理效果

图5 不同滤波算法对污染度为0.2 的pepper图的处理效果

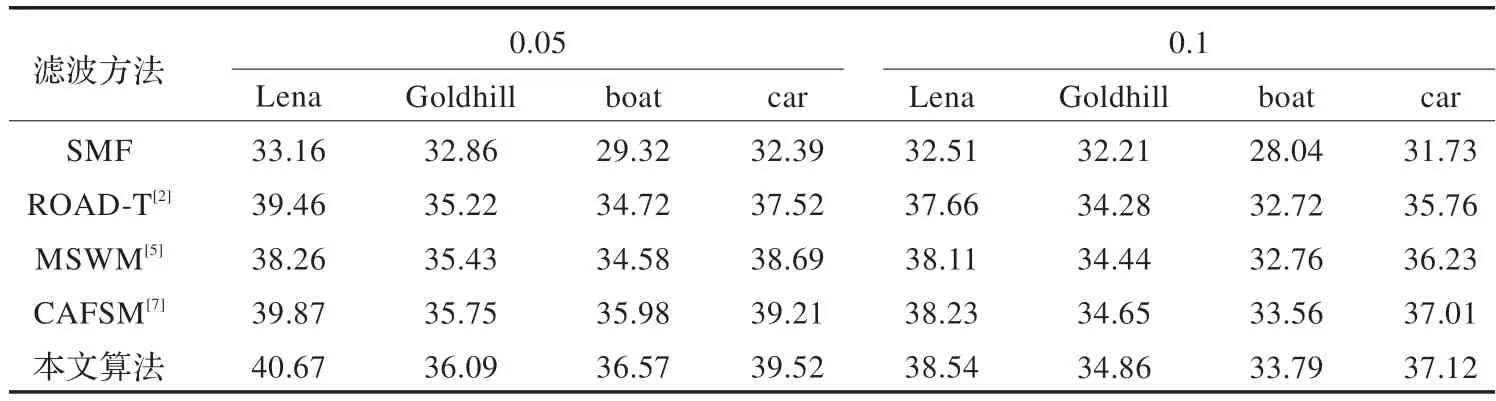
表1 不同滤波方法处理污染度为0.05 和0.1 的四幅图像的PSNR 值比较

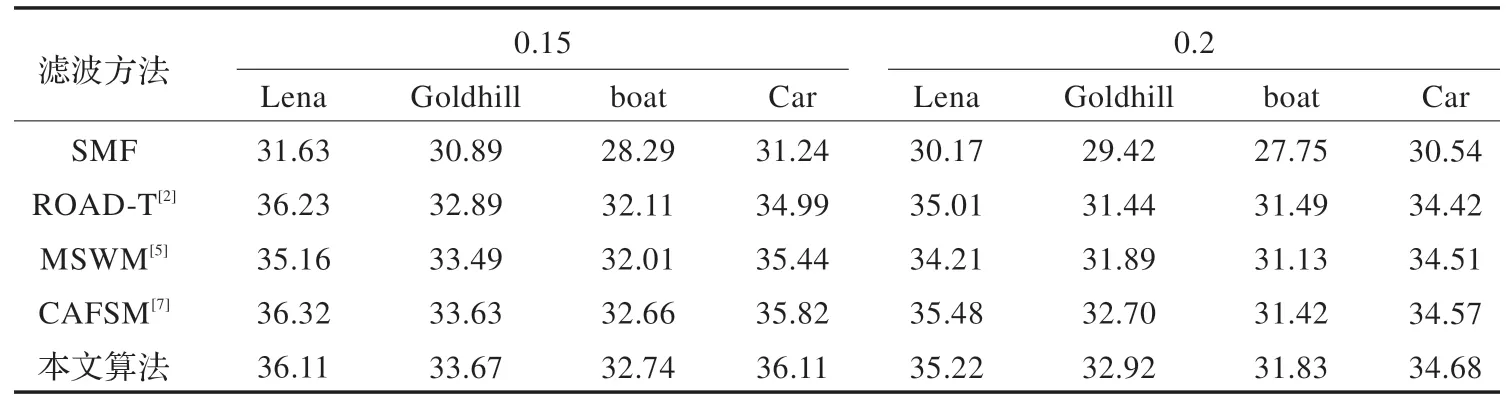
表2 不同滤波方法处理污染度为0.15 和0.2 的四幅图像的PSNR 值比较

图6 不同滤波算法对污染度为0.2 的boat图的处理效果

（2）客观评价

为了更客观地比较算法的处理效果，用峰值信噪比（Peak Signal to Noise Ratio，PSNR）来作为标准评价，其计算如式（9）。

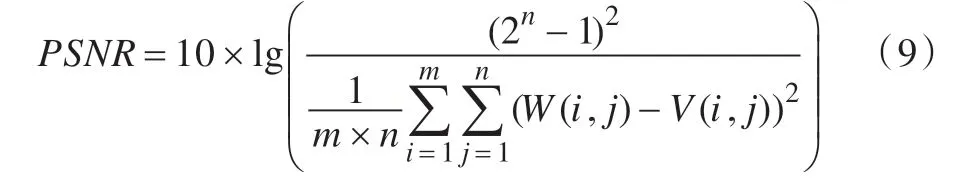
其中，W(i，j)表示原图像像素值，V(i，j)表示滤波后图像的像素值，图像大小为m×n。

表1、表2 是不同污染度的Lena、Goldhill、boat 和car四幅图像对于不同处理方法的PSNR 值比较。图7 以图形方式给出了Pepper 图像对于不同处理方法的PSNR值比较，由于SMF 的滤波效果比较差，所以在图中只与其他三种算法进行比较。

由表1~2 中数据可知，本文算法具有良好的滤波效果，尤其是在噪声污染度较小的情况下。对于噪声污染度小的图片来说，在进行相关矩阵计算时噪声点和正常像素点之间的相互影响较小，所以在对相关矩阵进行聚类分离噪声时，可以很好地分离出噪声，滤波效果较好；随着噪声污染度的增大，噪声点与正常像素点之间的相互影响增大，所以在计算相关矩阵时，容易混淆噪声点与正常像素点，因此在聚类时不能准确地分离出噪声点，导致噪声点的漏检和误检，滤波效果稍差，这也是本文需要改进的地方。

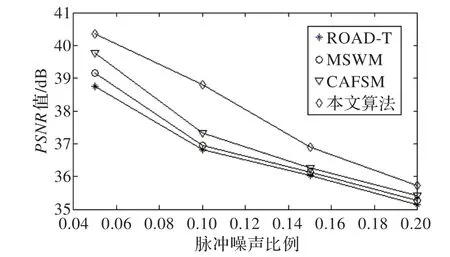
图7 针对加入不同污染度的随机值脉冲噪声的样本图像“Pepper”，四种算法的PSNR 值比较

5 结论

本文提出了一种应用模糊C 均值聚类算法对噪声图像进行噪声分离的滤波算法。运用图像中正常像素点的相似性和噪声点的孤立性对正常像素点和噪声点进行相关计算，将噪声图像转换为相关矩阵，最后运用模糊C 均值聚类算法分离出噪声点并用中值取代噪声点。通过大量实验并与近年来优秀的中值滤波算法做比较，结果表明，本文算法在低污染度情况下能更好地检测出噪声点，滤波效果更好。

[1] Sun T，Neuvo Y.Detail-preserving median based filters in image processing[J].Pattern Recognition Lett，1994，15：341-347.

[2] Garnett R，Huegerich T，Chui C，et al.A universal noise removal algorithm with an impulse detector[J].IEEE Trans on Image Process，2005，14（11）：1747-1754.

[3]邢藏菊，王守觉，邓浩江.一种基于极值中值滤波的新型滤波算法[J].中国图形图象学报，2001，6（6）：533-536.

[4] Zhang S，Karim M A.A new impulse detector for switching median filtering[J].IEEE Signal Processing Letters，2002，9（11）：360-363.

[5]Kang Chung-Chia，Wang Wen-June.Modified switching median filter with one more noise detector for impulse noise removal[J].AEU-International Journal of Electronics and Communications，2009，63（11）：998-1004.

[6]陈守水，杨新.一种基于两阶段的脉冲噪声滤除算法[J].信号处理，2008，24（4）：627-630.

[7] Toh K K V，Isa N A M.Cluster-based adaptive fuzzy switching median filter for universal impulse noise reduction[J].IEEE Transactions on Consumer Electronics，2010，56（4）：2560-2568.

[8] Lin Yuewei，Fang Bin，Tang Yuanyan.Image restoration using fuzzy impulse noise detection and adaptive median filter[C]//2010 Chinese Conference on Pattern Recognition（CCPR），2010：1-4.

[9]Dong Y，Chan R H，Xu S.A detection statistic for randomvalued impulse noise[J].IEEE Trans on Image Process，2007，16（4）：1112-1120.

[10] Yu Zhiding，Zou Ruobing，Yu Simin，et al.Noise-robust binary segmentation based on ant colony system and modified fuzzy C-means algorithm[C]//IEEE Congress on Evolutionary Computation，2009：2488-2493.

[11] Singh K M，Bora P K，Mahanta A.Features preserving filters using fuzzy Kohonen clustering network in detection of impulse noise[C]//Proceedings of IEEE Region 10 International Conference on Electrical and Electronic Technology，2001：420-423.

[12]Sulaiman S N，Isa N A M.Denoising-based clustering algorithms for segmentation of low level Salt-and-Pepper noise-corrupted images[J].IEEE Transactions on Consumer Electronics，2010，56（4）：2702-2710.