中国股市收益波动特征分析*

张海燕 何大强

（长春工业大学基础科学学院 吉林 长春 130012）

一、引言

在现实的金融市场里，资产收益率序列的波动性经常表现出波动聚类和杠杆效应，资产收益率的分布表现出高峰厚尾的特性，这些特征明显违背了传统模型中收益率服从正态分布及收益率的方差不随时间变化的经典假设。为了有效地模拟这些特征，Engle（1982）首次提出了自回归条件异方差（AutoregressiveConditionalHeteroskedasticityARCH）模型，Bollerslev在1986年ARCH模型基础上提出了推广的自回归条件异方差（GARCH）模型，GARCH模型很好地刻画了多数金融时间序列的异方差性和波动高持续性以及收益率服从高峰厚尾分布等特性，成为经济计量中研究波动性的重要工具。随着GARCH模型的不断发展和对金融序列波动性的研究的逐渐深入，发现传统的GARCH模型对金融时间序列的波动持续性的描述存在着一定的局限性，从传统GARCH模型估计得到的结果表明波动具有很高的持续性的特征，在建模过程中若不考虑时间序列中的结构变化，容易导致条件异方差过程产生伪持续性，其表现为模型估计结果是IGARCH（IntegratedGARCH）模型或者条件异方差过程具有长记忆性（longmemory）。另外，因为标准GARCH模型的估计方法，如拟最大似然估计（QMLE）、广义矩估计（GMM）都要求模型参数和非条件方差在样本期内是保持不变的，因此如果样本期内时间序列发生结构突变，那么这些估计不仅会失效，而且也会影响到时间序列的非条件高阶矩的存在性和模型的预测能力。Hsu等最早开始时间序列方差结构变点的研究，并在最近二十多年里得到了深入发展，有许多研究者将这一研究拓展至GARCH模型，SV模型等时间序列模型中。美籍华人邹至庄于1960年提出了Chow’s断点数理检验方法，其思想是对每个子样本分别独立拟合方程与全样本方程比较，观察两组方程的残差平方和。在我国针对中国股市波动性结构突变诊断的研究并不是很多，张世英和柯珂（2002）使用分整增广GARCH-M模型分段建模方法检测了上证指数的结构性变点，计算量较大且变点来源不明。陈浪南和黄杰鲲（2002）从深成指数的日收益率序列入手，使用迭代累积平方和算法，检测到序列中的方差结构变点，并分段建模考察了利好消息和不利消息的非对称影响。杜江、赵昌文和杨记军（2003）采用迭代累积平方和MV算法对沪深股市的结构变点进行了检测，均发现了30余个结构变点。田铮儿、王红军和韩四（2008）对残量累积和检验统计量推广到GARCH（p，q）模型，利用新检验统计量对浦发银行股票价格序列进行了单一结构变点实证分析。叶阿忠、倪小平和周杰（2007）均利用修正迭代累积平方和算法检测出沪深A、B股指数收益序列的方差结构变点。本文将利用Chow’s断点检验方法系统检测上证指数收益的方差结构变点，并详细分析其与经济或政治事件的关联，证明结构性变点的来源。

二、上证综指收益率结构性变点检验分析

（一）样本选取和数据来源 为了研究我国股市波动的变化特征，选取我国上证综指作为主要研究对象，样本期为1990年12月19日至2011年4月13日共4975个观测值的日收盘价格的时间序列作为样本。（数据来自于新浪财经网站。原始序列为日收盘价格数据，取上证综指取对数收益率，即分别对上证综指进行自然对数一阶差分的处理：rt=lnpt-lnpt-1。其中，rt表示第t期收益率，pt表示第t期收盘价。

（二）描述性统计 从表（1）中的描述性统计数据可以看出上证综指的峰度141.0797远远大于3，而且Jarque-Bera统计量都拒绝了原假设的正态分布，呈现高峰厚尾的特征。Ljung-Box（12）统计量54.006显示上证综指收益率都存在显著的相关性，同时ARCH-LM（4）统计量21.2556显示上证综指收益率存在显著的ARCH效应。ADF检验显示上证综指收益率拒绝了单位根的原假设，因此收益率序列是平稳的。综上所述，对这上证综指收益率序列进行GARCH建模是合适的。

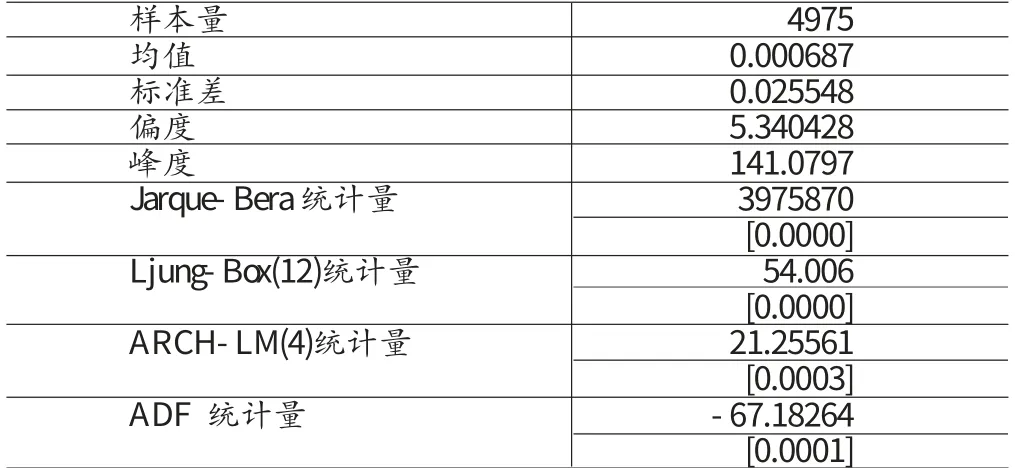
表1 上证综指收益率的描述性统计分析

（三）上证综指收益率波动的结构变点检测及原因分析 首先介绍Chow分割点检验模型。Chow分割点检验的基本原理是先将样本观测值根据分割点划分成两个或两个以上的子集，且这些子集所包含的观测值的个数必须大于方程待估计参数的个数；然后使用每个子集的观测值和全部样本的观测值分别估计方程；最后比较有约束的残差平方和与无约束性的残差平方和，判断模型的结构是否发生了显著性变化。其中使用F统计量和LR统计量进行检验，在无结构变点的原假设下，LR统计量渐进服从x2分布，其自由度等价于分割点个数乘以模型待估计参数的个数。以一个断点为例Chow检验统计量计算如下：

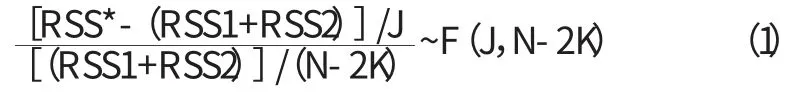
其中RSS*表示受到约束的整个样本下的残差平方和；RSS1是第一个子样本下的残差平方和；RSS2是第二个子样本下的残差平方和；K是回归中变量个数，包括常数项；N是整个样本的观测期。其次分析上证指数收益的波动结构变点。从图（1）中可以明显看出上证指数存在着收益率的结构变点，为了准确找出这些结构变点，本文采用chow检验方法进行结构分析。图（2）是其中一个检验结果，其他几个断点用同样的方法检测得出，所有结果见表（2）。下面从历史记录中找出发生在这7个时点附近的重大事件。第一个，我国股市的初期发展存在很多规则制定不全面、交易不规范并且股市规模较小等特点，在“邓小平南巡讲话”后对我国股市进行肯定的重大历史条件下，我国在1992年5月20日全面取消了股市的涨跌幅限制第二天（5月21日）沪市全面开放股价，先前受到涨限制的新股顺势暴发，上证指数从1992年5月20日的616.64点直接上升到收市的1265.79点，涨幅达105%。第二个，1994年7月30日中国证监会“三大救市政策”出台：年内暂停各种新股的发行与上市、有选择的对资信较好的证券机构进行融资、逐步吸引外国基金投入A股市场。受这些利好刺激，股市经历了比较疯狂的一天，沪、深两市场飙升达30%。第三个，1997年8月15日，国务院做出决定，沪深交易所划归中国证监会直接管理；中国证监会任命屠光绍为上海证券交易所总经理。1997年10月8日，国务院举行第62次常务会议，原则通过《证券投资基金暂行管理办法》；1997年10月23日，中国人民银行第三次降低存贷款利率，年存贷款利率的平均降幅分别为1.1%和1.5%。第四个，2006年11月20日，上证指数重新突破了2000点大关；2006年12月14日，上证指数创下了自创立16年以来的新高，达到2250.32点；2006年12月26日，沪指收报2505.32点，当日成交额达到457.9亿元，首次突破了2500点高位。2006年12月起，中国股市真正进入了长达约一年的疯涨的“牛市”行情，并在2007年10月16日创出历史最高6124.04点。第五个，2008-11-21受美国次债危机和金融危机的影响，2008年以来，我国A股市场一直保持单边下跌行情，上证综指自1月2日的5272.81点一直下跌，美国雷曼兄弟银行倒闭，美国股市暴跌，央行下调银行准备金和贷款利息，致使金融股大幅下跌，上证指数跌破2000点，9月18日跌至1802.33点至10月28日的最低点1664.93点，跌幅超过68%，居新兴市场前列。中国出台紧急救市策略止跌。第六个，自上证综指于2008年10月28日跌至最低点后，我国股市开始缓慢上扬，走出了将近持续11个月的下跌行情，并且陆续开始上升。第七个，2009年7月29日，金融危机全面爆发以来全球最大一单IPO中国建筑在沪市登陆，上海证券发生了有史以来3031.75亿的最大单日成交量，并出现2009年最大跌幅，盘中连破3400、3300、3200整数关，报收3266.43点。2009年8月26日国务院常务会议研究部署抑制部分行业产能过剩和重复建设，引导产业健康发展。从图（2）中，能更直观地发现我国股市这十几年来发展过程中波动的阶段性变化。

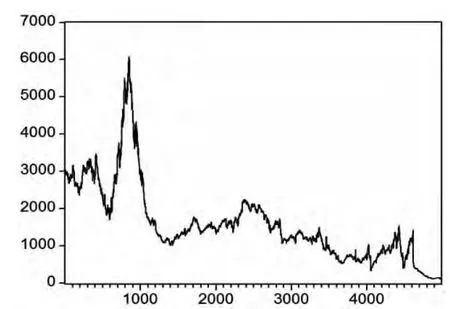
图1 上证指数收盘价的时间序列图

图2 Chow 检验结果

三、上证综指收益率序列检验分析

（一）描述性统计 根据上文基于chow检验检测出来的7个结构变点，依次将原收益率时间序列分为8个子样本：S1、S2、S3、S4、S5、S6、S7、S7、S8。从表（3）中的数据可以看出8个样本区间均具有不同的均值和标准差，而且差异较大，偏度、峰度和Jarque-Bera统计量都表明这8个样本区间的日收益率具有明显高峰厚尾的特征，且不符合正态分布。因此，采取分段建模是合理的。

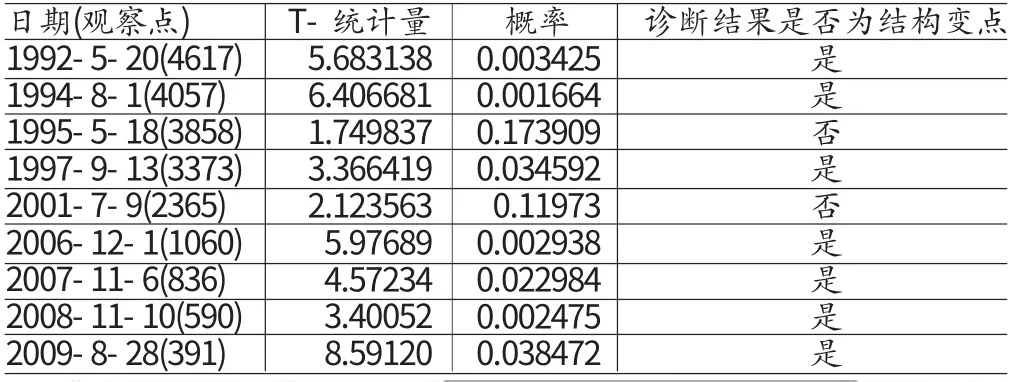
表2 chow 变点检测方法的检测结果

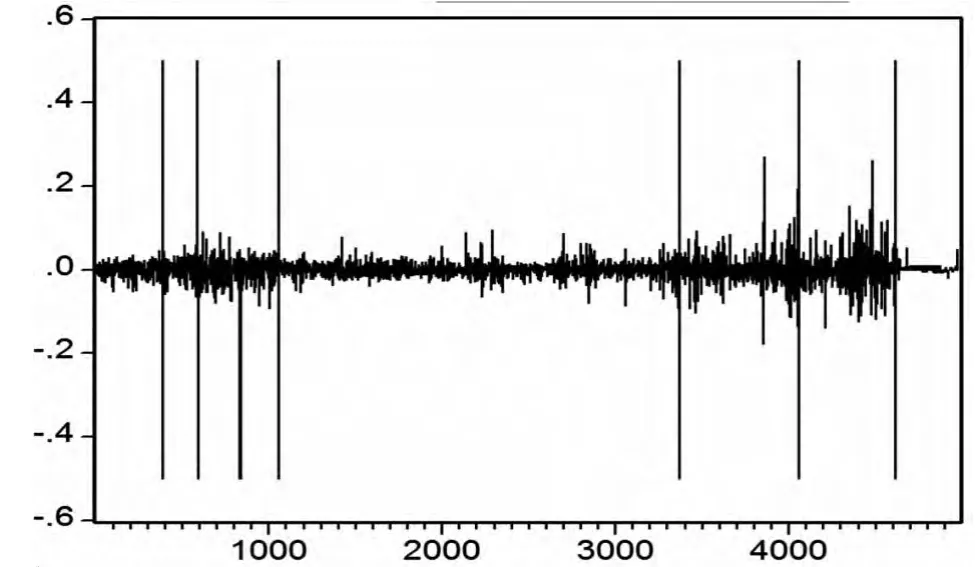
图2 上证综指收益率波动的结构变化阶段的划分,从图中可以发现有明显的波动聚集现象

（二）ADF单位根检验 从表（4）中ADF单位根检验的结果，可以发现各子样本区间的收益率序列t统计量均不超过1%，都拒绝了存在单位根的原假设，所以各子样本子序列仍是平稳的。并且Ljung-Box检验的修正Q统计量表明，总体样本的Ljung-Box检验都在5%的显著水平上拒绝了原假设存在12阶序列不相关，各个子样本区间S1至S8的Ljung-Box检验均接受了原假设，表明这8个子样本区间的收益率序列不存在自相关。这表明随着我国证券市场的发展和市场有效性的逐渐增强，我国市场体系逐步走向成熟。而ARCH效应的检验结果表明除了子样本区间S3、S4和S7外，其他5个子样本区间内的收益率序列都存在显著的异方差性。阶段S3和S4刚好分别对应着2006年底至2008年初的大牛市行情与2008年初至2008年11月份的大熊市行情，这表明在股市大涨或者大跌的背景下，序列都呈现为平稳的白噪声过程。

（三）自相关函数分析 从图（3）可以得出，上证综指日收益率的平方序列的自相关函数（ACF）并不是呈现指数衰减，而且在滞后阶数达到80时，它的自相关函数值（ACF）仍然是显著且不为零，这表明上证综合指数收益率的波动性呈现有长记忆性特征。观察图（4），可以发现S7、S7、S8子样本区间的平方收益率序列的自相关函数（ACF）基本成指数衰减的形式，原上证综合指数收益率平方序列中的长记忆特征已经消除。这表明上证综合指数收益率的波动实际上具有“伪长记忆性”的特点。

（四）分段GARCH诊断分析 对子样本S1、S2、S3到S8进行分段进行GARCH建模。模型形式、估计结果、诊断结果见表（5）。建立ARMA（m，n）-GARCH（p，q）的模型，同时考虑到我国股市的日收益率序列具有可偏、高峰厚尾性与非对称等特点，所以考虑序列残差服从偏广义误差分布（SkewedGeneralizedErrorDistribution，简记为skew-GED）。根据表（5）的数据结果，可以发现下述结果：（1）除了子样本区间S1、S2、S3的估计结果中参数ω 未能通过t检验以外，其他参数在5%水平上都是显著的。其中，偏度参数ξ 在子样本区间S1和S6里的值分别是1.112和0.9092，同时峰度参数v在全样本还是在各子样本区间的值都在1左右，这也表明考虑残差服从偏广义误差分布是合适的。此外，在各样本区间的模型诊断结果中，除了S2、S6的残差ARCH-LM检验在滞后阶数为10时的情况下概率大约为5%外，其他各残差诊断检验都接受了残差序列没有相关性和无ARCH效应的原假设，这也表明用GARCH模型描述各阶段收益率的波动情况的效果比较好。（2）观察描述性波动的持续性参数，α+β，各样本区间波动的持续性的参数全部小于总样本条件下波动持续性的参数，且总体样本波动的持续性的参数的值等于0.984218，非常接近于1，这表明全体样本收益率波动实际上具有很高的持续性，这时的模型与IGARCH模型同样比较接近。子样本区间的持续性参数的（除去无效的分段）最大值为0.09789，最小值为0.707633，与整体建模相比，参数的值显著减小，这与Lamoureux&Lastrapes在1990年的结论是一致的。这表明如果忽略我国股市收益率波动的结构突变性特征，盲目使用GARCH模型建模可能会导致股市波动的持续性会被高估，出现伪高持续性的现象，或伪IGARCH效应。（3）观察无条件方差ω/（1-α+β），总体样本无条件方差为6.42154E-06，表5中的各子样本区间的无条件方差为2.007E-05、9.316E-06、8.432E-05、0.000166、7.48E-06、7.56E-05、9.316E-06和4.98E-06，发现总体样本的无条件方差和子样本的无条件方差有比较大的差异，这也表明上证综合指数存在方差结构变点。（4）进一步分析各样本的系数α 和β。α 系数越大表明股票波动对市场反应越迅速，越剧烈，在条件异方差序列图中反映出的波动是长又尖的。通过表（5）中8个样本区间内α 的变化，发现（除S2、S4）α 是逐渐增大的，这表明我国的股市波动正在慢慢减缓。β 系数越大表明市场对条件异方差的冲击反应经过的时间越长，波动的持续越久。通过表（5）中8个子样本区间内的β 变化情况，同样可以发现（除S2、S4）β 有逐渐减小的趋势，表明股市的波动的持久性正在增强。

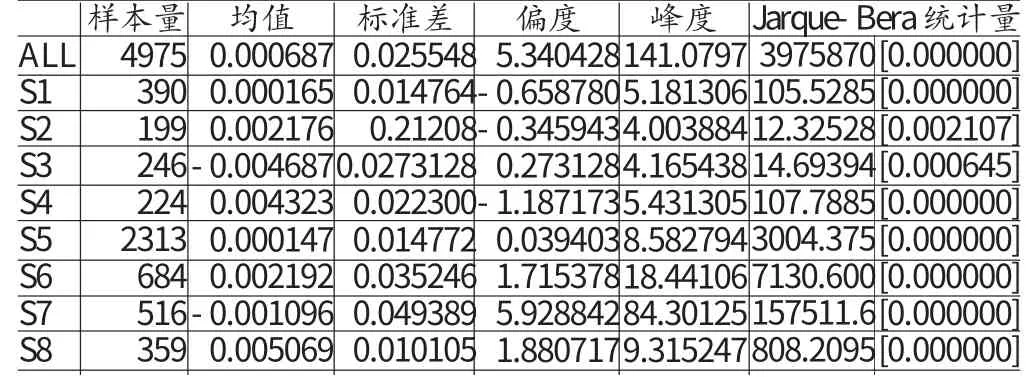
表3 上证综指各阶段收益率序列的描述性统计量

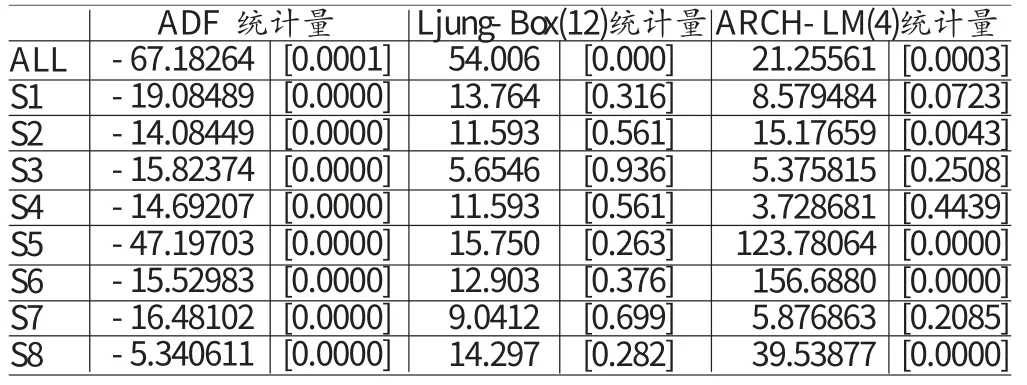
表4 上证综指各阶段收益率序列的平稳性检验、时序相关性检验和ARCH 效应检验

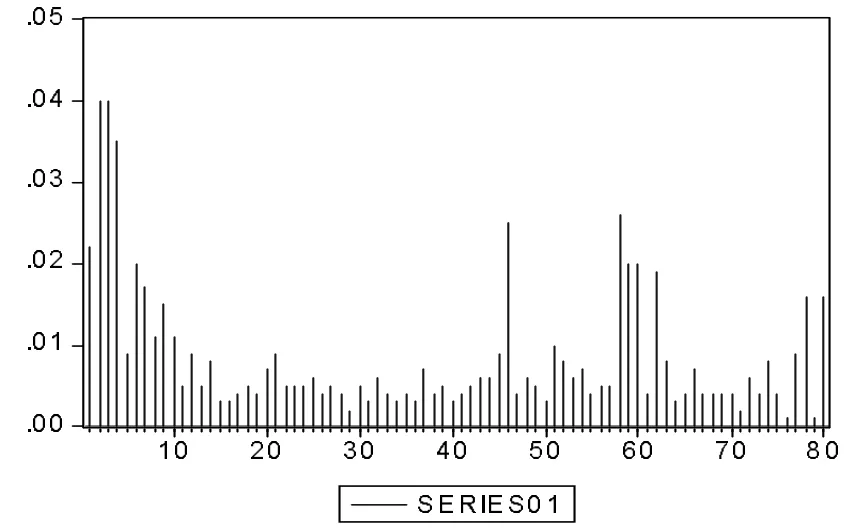
图3 上证综指日收益率平方序列自相关函数图

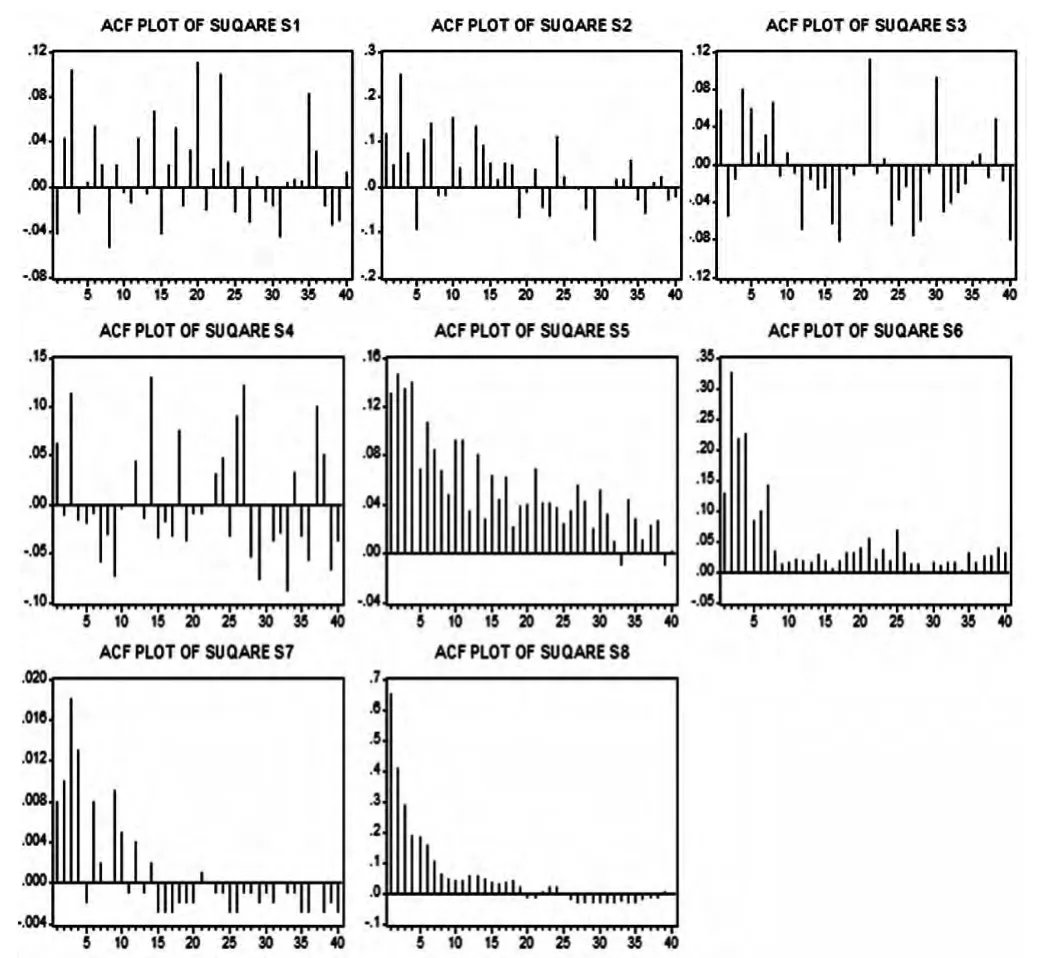
图4 上证综指各阶段收益平方序列的自相关函数图

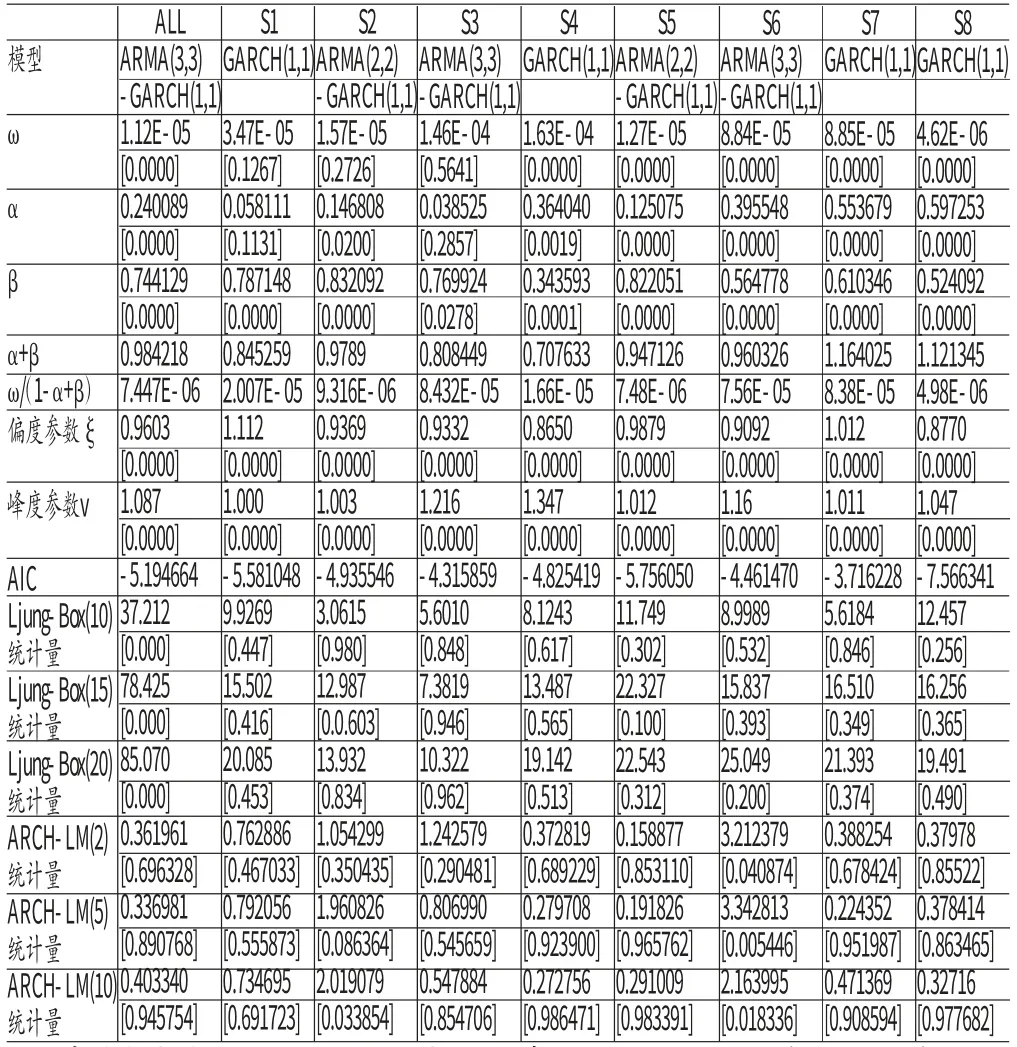
表5 上证综指各阶段收益率序列GARCH 建模的参数估计和模型诊断结果

四、结论

针对上证综合指数的收益率序列存在尖峰厚尾、非对称、异方差、长记忆性和高持续性等特点，本文使用chow分割点检验检验收益率序列中的方差结构变点，然后分析中国股市收益率的波动的结构性变化的情况，可以得出以下的结论：首先，根据chow分割点检验找到7个结构突变点将样本分为8段，所以对收益率序列进行了分段建模。发现在分段建模前，上证综指收益率的平方序列有很明显的长记忆性的特点；分段建模后，在每个子样本区间内的长记忆性的特征基本消除了。同时发现在1997年8月15日至2007年11月16日的“大牛市”阶段和2007年11月17日至2008年11月10日的“大熊市”行情段内，收益率接近白噪声序列（一个具有有限均值和有限方差的独立同分布的随机变量序列），即不存在自相关性同时也不存在ARCH效应。所以本文使用GARCH模型对其他子样本区间进行建模，发现在总体样本条件下，GARCH模型的持续性参数达0.9842188，很接近于1，所以模型接近于IGARCH模型形式，表明收益率波动有很高的持续性；在对各个子样本区间进行GARCH建模以后，子样本区间的波动持续性有明显下降。所以通过分段进行建模后，原序列的伪长记忆性和伪高持续性的特征已经消除了。另外，经过比较每个分段无条件方差，本文还发现，自1997年以后，2007年11月18日至2008年11月10日的“大熊市”该阶段的无条件方差8.432E-05要明显大于其他阶段的无条件方差。这表明因为市场的恐慌作用与“羊群效应”，“大熊市”（即大跌）行情里我国股市的波动性更加剧烈些。其次，通过对每个阶段GARCH模型结果中的参数变化的分析，发现中国的证券市场的波动性正在慢慢减缓，市场正在逐步走向成熟。事实上由于在我国股市发展初期，因为股市的规模较小，投资者的风险意识比较淡薄，股票市场存在着大量的不理性投资行为，所以市场的波动也较剧烈，然而政府通过颁发的一系列政策法律法规，证券市场的剧烈波动有效地遏制住了。通过分析方差结构变点前后一段时间内的重大政治、经济事件，发现从1992年5月以后，我国国内的政策的重要调整与宏观经济环境的重大变化都会引起我国股市波动的结构性变化；然而从2005年我国开始股权分置改革的逐步完成以及合格的境外机构投资者规模的不断扩大，中国股市波动的结构性变化越来越明显会受到国际经济环境变化与周边股市的冲击和影响，跟国际证券市场的一体化的倾向也趋于明显。

［1］张世英、柯珂：《ARCH模型体系》，《系统工程学报》2002年第3期。

［2］陈浪南、黄杰鲲：《中国股票市场波动非对称性的实证研究》，《金融研究》2002年第5期。

［3］倪小平、叶阿忠：《上海股票市场收益率波动性的结构转换分析》，《福州大学管理学院，工作论文》2007年。

［4］赵昌文、杜江、杨记军：《中国股市估值收益序列的结构性变点与重大事件反应》，《四川大学工作论文》2003年。

［5］韩四儿、田铮、王红军：《GARCH模型参数变化的残量检验》，《应用概率统计》2008年第2期。

［6］林光平（美）著，杨大勇译：《计算计量经济学》，清华大学出版社2003年版。

［7］R.S.Tsay.Analysis of Financial Time Series（2sd edition）John Wiley&Sons，Inc，Hoboken，New Jersey，2009.