基于解析信号振幅识别磁源体边界的分析解释方法

吴文贤，王永华，吴振波，杨 剑，焦彦杰，邓 珂

(成都地质矿产研究所，四川 成都 610081)

对于非线性非平稳信号，一种通常的方法就是假定信号为平稳或分段平稳的，然后采用适当的分析方法，如短时傅里叶变换、小波变换等对信号进行分析。这类分析是以傅里叶变换为基础的，而基于傅里叶变换的传统方法对信号作了许多假设和要求，如假设信号为高斯信号，噪声为高斯白噪声，大地系统为线性最小相位系统等处理的为稳态信号［1］，因此，该方法具有很大的局限性。另外，傅里叶变换中的频率代表着信号的周期性，而非平稳信号的特点之一就是没有周期性［2］，而且按照傅里叶变换的方法对信号进行分析将缺乏物理基础。

解析信号处理本质上是一种全通滤波器，也是信号分析处理中的一种重要方法［3］，基于解析信号更适合分析非平稳信号。对信号进行Hilbert变换，求出解析信号再对其相位求导，从而得到一个具有频率量纲的参量，在满足单值性的条件下，这个参量可以定义为瞬时频率，并且与Fourier变换的频率是相容的(谭善文等，2004)。其振幅比基于傅里叶变换的振幅更精确、更符合位场信号的实际情况，它代表了整个信号在时间跨度上幅值的累积效应，能有效地把数据的动态变化过程刻画出来。早在七十年代初期，希尔伯特变换方法已被引入到重磁场解释领域后［4］，解析信号处理在重磁异常正反演解释中的应用获得了较大的发展。Nabighian［5］最早借助于解析信号振幅由磁场的水平分量(垂直分量)求取垂直分量(水平分量)，Stanley等［6，7］提出一种以磁场水平和垂直梯度为基础的解释方法，Mohan 等和 Sundararajan 等［8，9］把解析信号处理用于位场定量解释中，Sundararajan等［10］利用改进的解析信号研究了关于自然电位解释理论中场源定位问题。解析信号具有可利用位场资料的全部信息以及受背景场影响较小等特点，因此可以提高物探资料数据处理的精度［11～15］。

1 解析信号原理

设x(t)为实信号，构造一个具有相同能量和相同频率的复信号q(t)，且x(t)为q(t)的实部。设q(t)的虚部~x(t)为x(t)的希尔伯特变换，则q(t)可以表示为:

则定义解析信号振幅E(t)为

相应地

若定义x(t)富氏变换为

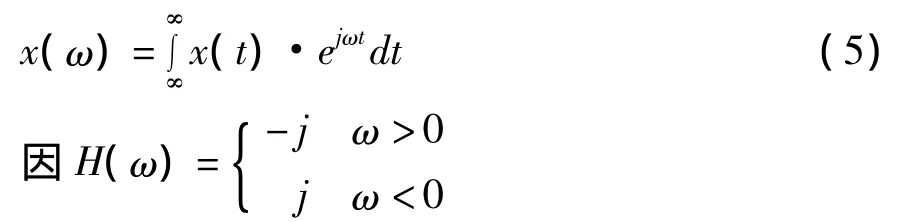
则(4)式变为

由上式可得

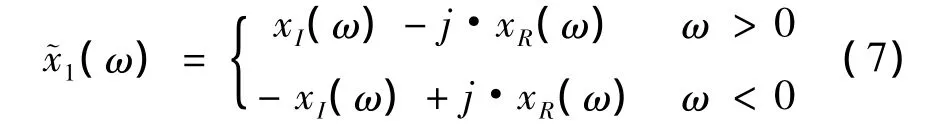
对于实函数，其富氏变换的实部是偶函数，虚部是奇函数，故应有

将(6)、(8)两式代入，并整理得

若令x2(ω)=－xR(ω)+jxI(ω)

根据(6)式，有

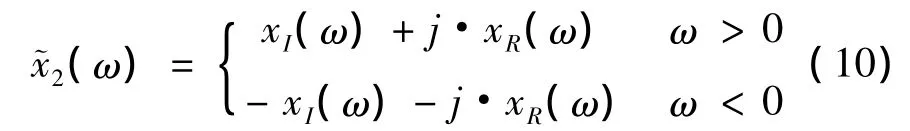
由此可见，可以对希尔伯特变换给予两种不同的定义式，即(9)和(11)式。

2 模型试验

2.1 二维组合模型

首先假设两个不同状态的二位模型，左侧模型设二维板状体上顶埋深20m，板宽40m，下延深度200m，板体倾角60°，已知地磁倾角为50°，板状体有效磁化倾角30°，有效磁化强度5000×10-3A/m;右侧模型设二维直立板状体上顶埋深50m，板宽60m，下延深度150m，地磁倾角50°，板体有效磁化倾角60°，有效磁化强度10000×10-3A/m。图1下半部分表示组合模型特征，其上半部分为组合模型正演磁异常(实线);对模型磁异常进行解析信号振幅处理，得到解析信号振幅(虚线)。可见，在组合模型中，两个模型中心分别与解析信号振幅峰值位置对应。

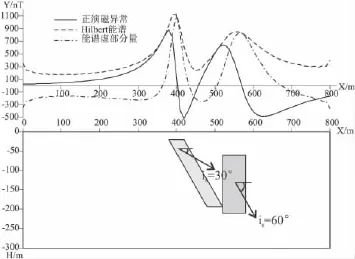
图1 二维组合模型磁异常分析图Fig.1 2D combination model for magnetic anomaly analysis

通过组合模型可知，解析信号振幅峰值位置与地磁倾角、地磁偏角及板状体产状无关，它与板状体中心位置关系密切。

2.2 三维组合模型试验

测线东西向，其一为直立棱柱体，中心坐标(350，350，100)，对应方向上的延伸长度分别为100m，100m和200m，地磁倾角45°，有效磁化强度为10000×10-3A/m;另一模型倾角60°，中心坐标(500，500，50)，对应方向上的延伸长度分别为100m，100m和300m，磁化倾角45°，有效磁化强度为5000×10-3A/m，图2为该组合模型异常分析结果，图中红色边框为模型上顶平面位置投影，图2a表示对应模型磁异常与模型上顶位置关系;图2b为对应的解析信号振幅。可见，图2a中模型位置与异常特征对应性不明，而图2b中的解析信号振幅中心与模型位置对应性较好，且模型位于振幅中心分布。

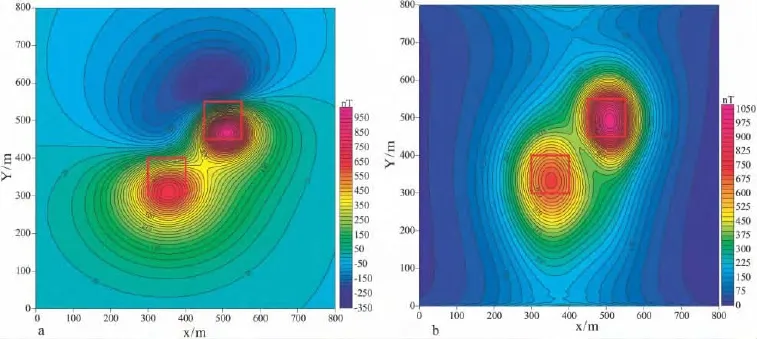
图2 三维组合模型异常分析图Fig.2 3D combination model for magnetic anomaly analysis

3 应用实例

老挝爬立山某铁矿区大地构造位置位于南海-印支地块的北部，地处南海西布康-昆蒿构造岩浆岩带的北西端。矿区内的构造较为复杂，主要由花岗闪长岩、花岗岩、闪长岩组成的岩浆岩系列构成环绕泥盆系碎屑岩-碳酸盐岩石的环形岩浆岩。在成矿作用阶段，以花岗闪长岩为代表的一系列中酸性岩浆呈基底式侵入，与上覆泥盆系碳酸盐岩-碎屑岩系列发生了广泛的接触交代作用，形成交代矽卡岩型透镜状矿体群。矿区内分布的主要地层有志留系、泥盆系和二叠系。236块物性标本测定显示，本区磁性最强属磁铁矿，次之为铁质砂砾岩和黄铁矿化磁铁矿;再次之为磁铁矿化、黄铁矿化、矽卡岩化围岩的磁化率值。围岩以碳酸盐岩、花岗闪长岩为主，其磁性远小于磁铁矿及磁铁矿化体的值(见表1磁性参数统计表)。综上所述，本区磁异常主要由磁性矿体引起，因此，磁法勘探在本区矿产勘查中十分有效。

表1 磁性参数统计表Table 1 Statistics of magnetic parameters

图3a中色块底图为该区实测△T异常平面图，○与●分别代表区内未见矿钻孔和见矿钻孔位置(均为直孔)。从图3a中可见，本区见矿钻孔位置与异常特征无对应性，在异常较强的位置反而未见矿;图3b为对图3a中的△T异常进行Hilbert变换得到的解析信号振幅异常，由图可见，经解析信号振幅处理后，异常中心整体北移，强异常相对集中，且范围增大;在区内的69个钻孔中，其中的13个未见矿的钻孔均位于解析信号振幅弱异常边缘或零异常带内，而剩余的56个见矿钻孔中，仅有2个在解析信号振幅弱异常带内(矿层厚度较小)，另有4个在解析信号振幅中强异常边界上，其余的50个均位于振幅异常中心。可见，该解析信号振幅能较好地反映矿体异常，可以通过解析信号振幅特征初步确定矿体分布位置。

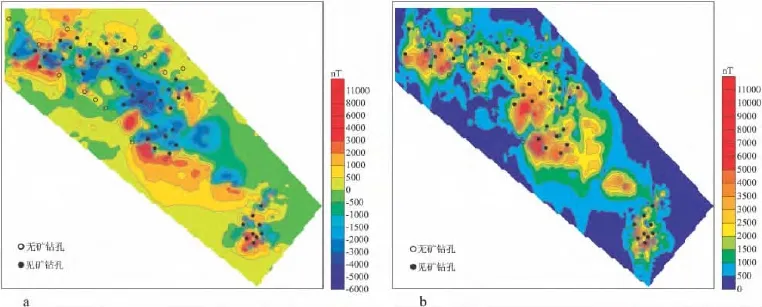
图3 老挝爬立山某铁矿区磁异常分析结果Fig.3 Magnetic anomalies of an iron ore district in Palishan，Laos

4 结论

通过对磁异常的解析信号处理，得到的解析信号振幅能有效圈定地下磁性体的中心位置和分布范围。在地质情况较为复杂的情况下，特别在低纬度地区，存在化极方法不成熟的影响时，该方法在分析平面磁异常展布及变化特征时更具优势。该方法原理简单、效果明显，更易于在现有位场转换程序中实现。理论模型和实际资料处理表明，该方法在低纬度地区能根据磁异常有效圈定地下磁性体的中心位置和分布范围。期望该方法在我国南海地区油气勘探及在东南亚国家境外地质找矿工作中为磁异常解释发挥积极的作用。

致谢

感谢成都地调中心的范文玉教授级高工、刘增铁教授级高工、邹光富研究员和高建华老师给本文提出的宝贵建议和意见及秦皇岛鑫河钢铁矿业发展有限公司(老挝)的大力支持。

［1］NABIGHIAN M N.The analytic signal of two-dimensional magnetic bodies with polygonal cross-section:its properties and use for automated anomaly interpretation［J］.Geophysics，1972，37(3):507－517.

［2］MOHAN N L，SUNDARARAJAN N，SESHAGIRI RAO S V.Interpretation of some two-dimensional magnetic bodies using Hilbert transforms［J］.Geophysics，1982，47(3):376 －387.

［3］STANLEY J M，GREEN R.Gravity gradients and the interpretation of the truncated plate［J］.Geophysics，1976，41(6):1370 －1376.

［4］STANLEY J M.Simplified gravity interpretation by gradients;The geological contact［J］.Geophysics，1977，42(6):1230 － 1235.

［5］HINOJOSAL J H，MICKUS K L.Hibert transform of gravity gradient profiles:Special cases of the general gravity-gradient tensor in the Fourier transform domain［J］.Geophysics，2002，67(3):766－769.

［6］YI LUO，SALEH Al-DOSSARY，MAHER M，et al.Generalized Hilbert transform and its applications in geophysics［J］.The Leading Edge，2003，22(3):198 －202.

［7］李媛媛，杨宇山.位场梯度的归一化标准差方法在地质体边界定位问题中的应用［J］.地质科技情报，2009，28(5):138－142.

［8］蔡剑华，龚玉蓉，王先春.基于Hilbert-Huang变换的大地电磁测深数据处理［J］.石油地球物理勘探，2009，44(5):617－625.

［9］谭善文，秦树人，汤宝平.Hilbert-Huang变换的滤波特性及其应用［J］.重庆大学学报，2004，27(2):9 －12.

［10］SHUEY R.Application of Hilbert transforms to magnetic profiles［J］.Geophysics，1972，37(6)，1043 －1045.

［11］刘洪学.磁异常的希尔伯特变换方法［J］.物探与化探，1985，9(5):392－395.

［12］杨建文，贾民平，许飞云等.一种改进的Hilbert能量谱算法研［J］究.中国工程科学，2005，7(7):55 －59.

［13］王硕儒，于涛.希尔伯特变换快速计算及其在磁二度体△T解释中的应用［J］.山东海洋学院学报，1985，15(3):67 －65.

［14］管志宁，姚长利.倾斜板体磁异常总梯度模反演方法［J］.地球科学，1997，22(1):81 －85.

［15］刘天佑.位场勘探数据处理新方法［M］.北京:科学出版社，2007.