过往车辆对人行天桥产生的追风效应原理及影响分析∗

赵锐，张毅刚

(1.新疆大学建筑工程学院，新疆乌鲁木齐830049；2.北京工业大学空间结构研究中心，北京100124；3.北京工业大学城市与工程安全减灾省部共建教育部重点实验室，北京100124)

0 引言

近年来，人行天桥的振动问题越来越受到人们的重视，因为这直接影响到桥上行人的感受.产生这种振动的振源主要有两个，一个是桥上的行人，另一个是桥下过往的车辆.对于人致振动问题，从2000年的千禧桥事件[1]开始国内外已进行了大量深入的研究，曾三次召开人行天桥国际会议，欧洲法、德等国也重新修订了人行天桥的设计指南和规范.对于车致振动问题，王柏生[2]、李东[3∼5]、张冠华[6]均通过现场实测研究了过往车辆通过地面传播振动对人行天桥的影响.而对于桥下净空高度处的气流运动对人行天桥的影响则较少有人研究.这种由于以一定速度行驶的车辆产生的气流运动而使人行天桥主梁产生振动的现象称为追风效应.Z´olowskiP[7]通过研究得到了卡车从桥下通过时，各种因素（包括车速、桥净空高、有无挡风板、车数及跟车距等）对人行天桥振动的影响分析.文献[8]只是主观预测追风效应对人行天桥有影响，但没有进行深入的分析，也没有理论依据.文章利用计算流体力学软件FLUENT对过往车辆从人行天桥下通过时产生的流场进行受力分析和速度矢量分析，提出追风效应的产生原理及对人行天桥的影响.

1 建立计算模型

1.1 计算原理

流场计算的基本过程是首先建立反映工程或物理问题本质的数学模型，然后在空间上用有限体积法将计算区域离散成许多小的体积单元，在每个体积单元上对离散后的控制方程组进行求解.

1.1.1 建立数学模型

文献[7]采用在工程流场计算中最常用的标准K-ε湍流模型，它忽略分子之间的粘性，假定流场完全是湍流.该模型主要是通过求解两个附加方程K方程和ε方程（其中K方程是湍流脉动动能方程，ε方程是湍流耗散方程）来确定湍流粘度，进而求解湍流应力.然后根据质量守恒定律和动量守恒定律建立的湍流时均连续方程和雷诺方程，在满足初始条件和边界条件的情况下，使方程组封闭，求解流体的速度分布.K、ε方程的张量形式如下.

K方程

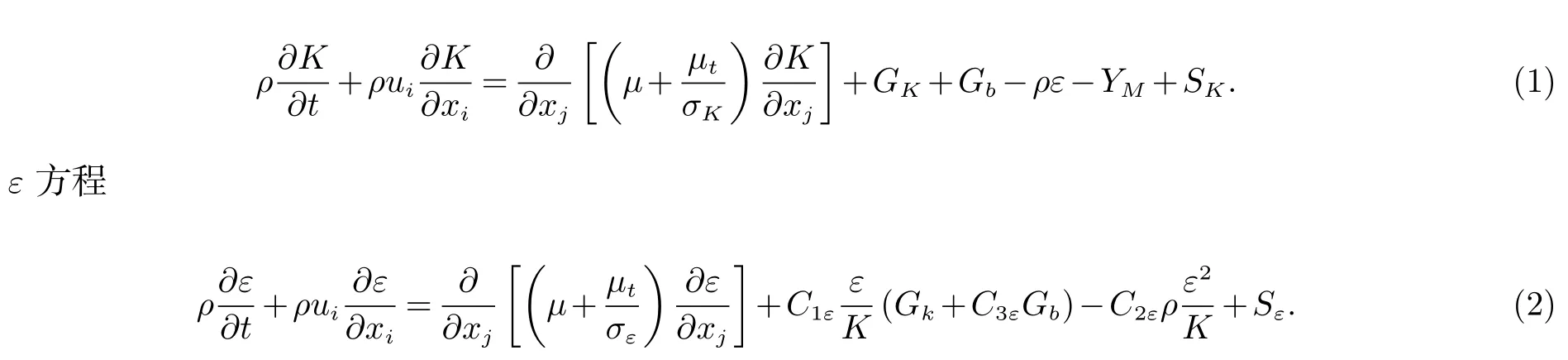
湍流粘度µt方程

式中GK表示由层流速度梯度而产生的湍流动能；Gb表示由浮力产生的湍流动能；YM表示可压缩湍流脉动膨胀对总的扩散率的影响；SK和Sε是用户定义的.方程中引入了三个系数C1ε、C2ε、Cu和两个常数σK、σε（K与ε的湍流普朗特数），目前这5个经验常数一般分别取1.44、1.92、0.09、1.0、1.3，常数C3ε为ε方程受浮力的影响程度.各量下角标i、j、k取值为1、2、3，分别对应x、y、z，k为求和下标.

1.1.2 建立离散方程并求解

用有限体积法，将所计算的区域划分成一系列控制体积，每个控制体积都有一个节点作代表，采用二阶迎风格式作为离散格式，通过将守恒型的控制方程对控制体积作积分来导出离散方程.

由于空气的流动速度较小，为亚音速流动，其马赫数M<0.3，所以可将空气视为不可压缩流体，对该离散方程采用分离解法，即不直接求解联立方程组，而是逐个地求解各变量代数方程组.具体方法采用应用最广泛的利用压力耦合方程组的半隐式方法(SIMPLE算法)实现的压力修正法，其求解基本过程如下：

（1）假定初始压力场；

（2）利用压力场求解雷诺方程，得到速度场；

（3）利用速度场求解时均连续方程，修正压力场；（4）解湍流方程及其他标量（速度、压力）方程；

（5）判断当前时间步上的计算是否收敛.若不收敛，返回第二步，迭代计算；若收敛，重复上述步骤，计算下一时间步的物理量.

1.2 模型参数设置

利用GAMBIT前处理器建立车辆、人行天桥及流场的二维网格模型.其中，车辆采用文献[9]中三轴客车的限值尺寸：长×宽×高=13.7 m×2.5 m×3.5 m（不包括0.5 m的离地间隙），人行天桥采用等截面钢箱梁，净空高5 m，顶板宽4 m，箱梁底面宽1.6 m，翼缘板端面高0.1 m，与箱梁交接处高0.36 m.车头和人行天桥左边界间的初始距离为两倍的车长.截取部分网格划分情况如图1所示，最小网格为0.8 m，网格总数2 834 048个.

图1 二维模型面网格

利用FLUENT 6.2进行基于有限体积法的瞬态流场分析.流体空气采用常温20◦C时的密度ρ为1.24 kg/m3，动力粘度µ为1.8e-5Pa·s.根据文献[10]的规定，城市快速路的最高车速为80 km/h，约为22 m/s.即用该模型模拟无风条件下车辆以22 m/s的速度从人行天桥下匀速通过.空气按其速度等物理量随时间变化的不可压缩非稳态流体进行分析计算，不考虑其重力的影响.

1.3 边界条件及计算域的设置

整个模型分为两个计算域，分别为人行天桥所在的“sky”域和客车所在的“road”域，如图2所示.其中“road”域采用滑移网格技术来模拟车辆的运动，图中虚线为滑移交界面.由于“road”域的滑移网格是车辆和空气一起以22 m/s的速度向右行驶，所以要在该域的右边界设速度为22 m/s的速度入口边界，同时将该域内的空气设为速度与该滑移网格运动方向相反的同速度作为初始条件.该域的左边界为出流边界，车辆距该边界的初始距离要大于四倍车长，保证不发生回流.该域比“sky”域长出的距离为车的行进距离.“sky”域为90 m×20 m，上边界为对称边界，左右两侧为周期边界.地面为壁面边界.

图2 边界条件及计算域的设置

2 追风效应分析

车辆以22 m/s的速度匀速行驶，行进距离为13.7×5+4=72.5 m，即从车头距离人行天桥左边界两倍车长处开始计算，至车尾超过人行天桥右边界两倍车长处为止，人行天桥左右边界间距即桥面宽度为4 m，共用约3.3 s，以0.01 s为时间间隔进行迭代计算.

2.1 受力分析

由迭代分析得到人行天桥各时刻横向力和竖向力的曲线分布图，如图3所示.横向力和竖向力分别为车辆行驶方向和竖直方向，图3中各峰值点所对应时刻车辆行进的位置见图4.

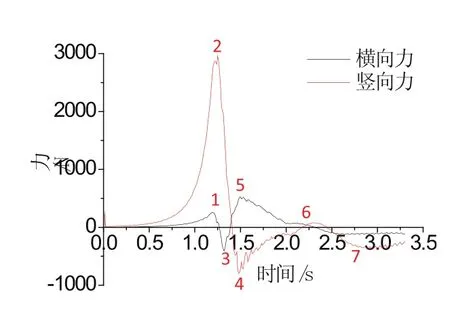
图3 人行天桥各时刻的横向力和竖向力曲线图

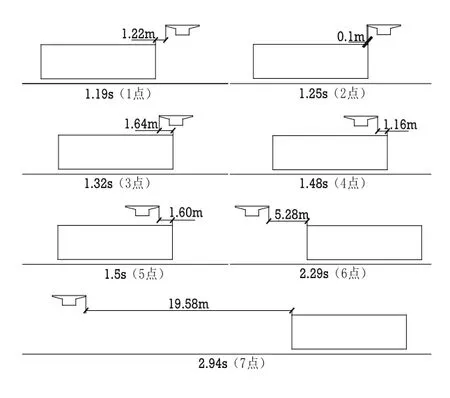
图4 车辆不同时刻的位置图

从图3中可以看出，峰值主要集中在中部，两端均有较长一段接近于零.这说明在模型中设置的车辆行进距离满足要求，可以反映过往车辆对人行天桥产生的气流影响的全过程，并保证车辆通过人行天桥下的空气流动为稳流，无回流.从图3和图4中可知，人行天桥受到的横向力和竖向力均分布于坐标轴的两侧，正、负压交替.

竖向力分析：当车行驶1.25 s时，车头超过人行天桥的左边界0.1 m，即图4的2点位置，这时人行天桥由于受到车辆向前推挤的气流的影响而达到竖向力的正向最大值.随着车辆的向前行驶，气流遇到人行天桥这一障碍物后产生绕流现象，对其压力大幅减小至负压，当车行驶1.48 s时，车头超出人行天桥的右边界1.16 m，即图4的4点位置，这时达到最大负压.最大正、负压时间相隔仅0.23 s.随着车离人行天桥越来越远，对其压力也随之减小， 但由于大气在整个计算域内的连通性，压力曲线还是会出现小幅的波动.6点为2.29 s，车尾超出人行天桥右边界5.28 m；7点为2.94 s，车尾超出人行天桥右边界19.58 m；4、6点间隔0.81 s，6、7点间隔0.65 s.

横向力分析：与竖向力相比，横向力对人行天桥的影响较小.车辆距人行天桥左边界1.22 m处为第一个正压峰值，即图4的1点.进入到桥面下的1.32 s这一时刻变为最大负压，即3点，两峰值时间间隔仅0.13 s.车头通过人行天桥右边界1.6 m处又达到第二个正向峰值，同时也是最大正压，即图4的5点，与最大负压时间间隔0.18 s.随着车辆离人行天桥远去，横向力越来越接近于零.

从以上分析可知，横向力和竖向力均不到1 s即可完成一个正负峰值的交替，而且竖向力的正向峰值要远大于横向力，因此，人行天桥相当于被施加了两个瞬时荷载.从图3中看，这种瞬时荷载表现为具有随机性质的脉动.这一竖向瞬时荷载正是导致人行天桥上下振动的直接原因.

2.2 速度矢量分析

以图4的2点、3点和4点三个时刻为例进行速度矢量分析，说明气流的运动方向对人行天桥的影响.三个时刻的流场速度矢量图如图5所示.图6为人行天桥钢箱梁截面上监测点的布置.图7为图6中各监测点分别在三个时刻的速度曲线图.

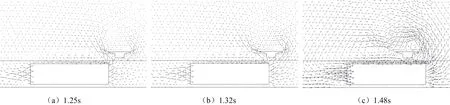
图5 某一时刻流场速度矢量图

图6 监测点布置图

图7 某一时刻各监测点的速度值

从图5（a）1.25 s这一时刻的流场速度矢量图中可以看出，车向前运动的同时，会挤压前方的空气而使一部分随车向前流动，另一部分绕到车的后方填补产生的负压区而形成环流.车到达人行天桥左边界时，由于随车一起运动的气流遇到了人行天桥这一障碍物而分别从人行天桥的左右两侧向上运动，对照图6中监测点的位置，从图7中可知，这一时刻的人行天桥左边界1点速度最大，右边界13点次之，此时，人行天桥受到了最大的升力.

随着车的继续前行，经过了0.07 s，当车头到达人行天桥中部图5（b）1.32 s这一时刻时，从右边界向上运动的气流在人行天桥顶部水平向左运动，与从左边界上升的气流汇合，此时为人行天桥所受到的横向力的负向最大值.从图7中此刻的曲线图可以看出，左边界1点的速度值要略小于右边界13点的值，说明左边界处的速度要略小于右边界的速度，也就是说，右边界处的气流有一大部分会向左运动与从左边界处上升的气流汇合，然后绕到车的后方形成环流，还有一小部分气流由于受到左边界处速度较慢的气流的阻碍而在桥面靠右边界的上方形成一个小环流，而使人行天桥受到一个较小的向下的速度.又经过了0.16 s，当车头通过人行天桥右边界，到达1.48 s这一时刻时，从图7中这一时刻的曲线图可知，左边界1点的速度值要比右边界13点的值小的多，虽然这两个值比前两个时刻的速度值都小， 但两者的差值此时最大，这说明如图5（c）所示的此时从右边界处上升的气流相比1.32 s这一时刻而言会有一大部分在桥面上方形成小环流而使人行天桥受到向下的速度，相对较少一部分气流与左边界处的上升气流汇合向车后方运动.这也是为何此时人行天桥受到竖向力负向最大值的原因.但由于在人行天桥的下方和两侧仍有向上的气流，所以这一负值要比最大正值小的多.

另外，从图7中还可以看出，各条曲线图中的3点、4点、5点的速度值都相同，9点、10点、11点的速度值也都相同，这几个点正好都是箱梁腹板上的监测点，而且从整条曲线上来看，其值都较小.这说明气流的运动对人行天桥的腹板影响较小， 由于翼缘板较短，气流不会在其下方形成环流，只是沿着腹板向上运动.

2.3 追风效应的原理

从以上的计算分析可知，流体的流动类型满足湍流的运动特征，即在运动过程中流体质点具有不断的随机的相互掺混的现象，速度和压力等物理量在空间上和时间上都是具有随机性质的脉动.基于流体力学的观点，可以得出在无风条件下人行天桥受到过往车辆产生的追风效应的原理：

（1）车辆以一定速度向前行驶的过程中，其前部空气受挤压而使压力升高，被排挤的空气一部分随着车辆向前流动，另一部分则向车辆后方流动填补车辆侧面及尾部的空气负压而形成环向流动；

（2）随着车辆的不断前行，当气流遇到人行天桥这一障碍物后，除部分气流随车继续前进外，其余的气流会从人行天桥两侧绕过继续向车后方运动填补负压区形成环流.此时，当人行天桥左侧气流的运动速度大于右侧时，人行天桥受到的竖向正压较大，而当左侧气流的运动速度小于右侧时，从其右边界绕过来的气流一部分与左边界处的气流汇合向车的后方运动，另一部分在桥面上方形成一个小的环流，人行天桥受到的竖向负压较大；

（3）车辆驶离人行天桥，但填补车辆后方的气流仍对人行天桥有影响，所以竖向力曲线此时仍有小幅波动；

（4）从人行天桥所受力的性质来看，横向力和竖向力都属于具有随机脉动性质的瞬时荷载.其中竖向瞬时荷载是导致人行天桥钢箱梁产生明显振动的直接原因.

2.4 影响分析

2.4.1 不同车速对人行天桥的影响

通过计算车辆以不同车速在无风条件下通过人行天桥使其受到的竖向力来分析追风效应对人行天桥的影响程度.相同车型，分别以12 m/s、15 m/s、18 m/s和22 m/s的速度从人行天桥下通过，用FLUENT软件计算竖向力随时间的变化曲线如图8所示，表1为图8中各条曲线的峰值时刻及对应的行进距离.

图8 不同车速下人行天桥的竖向力曲线图

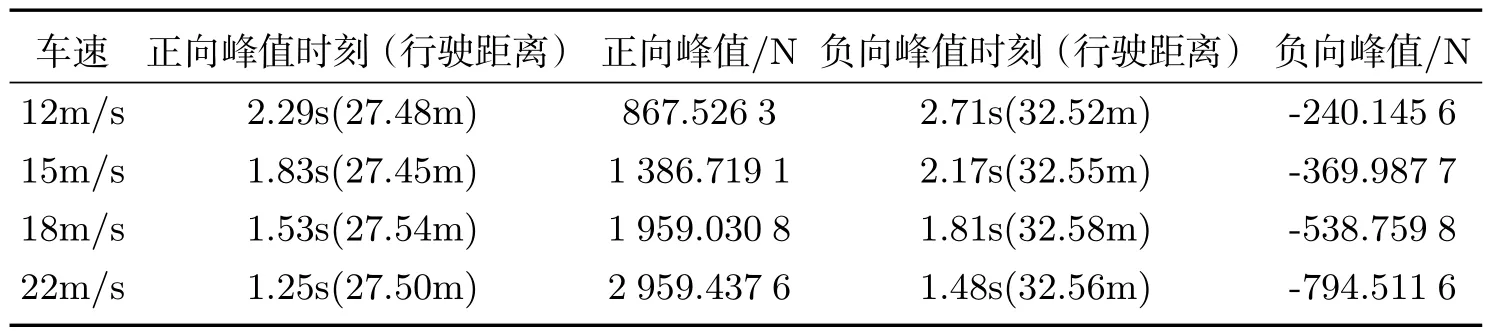
表1 不同车速下竖向力的峰值情况

对照图8和表1，从竖向力达到峰值的时刻看，车速分别为12 m/s、15 m/s、18 m/s和22 m/s时，竖向力达到正向最大值时车分别行驶了2.29 s、1.83 s、1.53 s和1.25 s；竖向力达到负向最大值时车分别行驶了2.71 s、2.17 s、1.81 s和1.48 s；即不同车速下，竖向力达到峰值的时刻是不同的.从竖向力达到峰值时车的行驶距离看，四种车速下，人行天桥的竖向力达到正向峰值时车的行驶距离分别为12×2.29=27.48 m、15×1.83=27.45 m、18×1.53=27.54 m和22×1.25=27.5 m，由于取0.01 s为时间间隔，所以车的行驶距离会有一定的误差，可认为四种车速下车辆是在同一位置达到竖向力的正向最大值的.同理，四种车速下，人行天桥的竖向力达到负向峰值时也可认为四种车速下车辆是在同一位置达到竖向力的负向最大值的.这一分析结论完全符合追风效应的原理.从峰值的大小来看，由表1可知，车速从12 m/s提高到22 m/s，竖向力的正负峰值提高3倍多.由此可见，车速对人行天桥竖向力的影响较大.

2.4.2 不同车型对人行天桥的影响

通过计算不同车型在无风条件下通过人行天桥使其受到的竖向力来分析追风效应对人行天桥的影响程度.大型车如前所述，长×宽×高=13.7 m×2.5 m×3.5 m（不包括0.5 m的离地间隙），另取一个小型车（轿车）：长×宽×高=5m×1.9m×1.375m（不包括0.125m的离地间隙），和一个中型车（载货车）：长×宽×高=7.4 m×2.2 m×2.4m（不包括0.2m的离地间隙），与该模型中的三轴客车以相同的速度22m/s、相同的计算行驶距离通过人行天桥.小型车、中型车和大型车与桥底面的净空高分别为3.5 m、2.4 m和1 m.用FLUENT软件计算竖向力随时间的变化曲线如图9所示，表2为图9中各条曲线的峰值时刻及对应的行进距离.

图9 不同车型下人行天桥的竖向力曲线图

表2 不同车型下竖向力的峰值情况

对照图9和表2，从竖向力达到峰值的时刻及相应的车辆行驶距离看，小型车、中型车和大型车使人行天桥的竖向力达到正向最大值的时刻分别为1.2 s、1.2 s和1.25 s，行驶距离分别为26.4 m、26.4 m和27.5 m；达到负向最大值的时刻分别为1.57 s、1.51 s和1.48 s，行驶距离分别为34.54 m、33.22 m和32.56 m.由此可以看出，三种车型相比，小型车先达到竖向力正向峰值，后达到竖向力负向峰值，大型车刚好相反，中型车居中，即小型车对人行天桥的影响时间要比中型车和大型车长.这是因为小型车车顶与人行天桥底面间的净空要比中型车和大型车大，当车辆向前运动推挤气流向其后方流动形成的环流遇到人行天桥时，小车形成的环流的直径要比中型车和大型车大，也就是说小型车在距离人行天桥较远处就开始对人行天桥有影响，同理，通过人行天桥后的影响距离也较长，所以小型车对人行天桥的影响时间要比中型车和大型车长，即先达到竖向力正向最大值，后达到负向最大值.这与追风效应的原理相符.从峰值的大小来看，由表2可知，人行天桥受到的竖向力正向峰值，大型车约为小型车的8倍、中型车的3.5倍，负向峰值也约为小型车的3倍、中型车的2倍.由此可见，车型对人行天桥竖向力的影响非常大，主要是车顶与桥底面净空高的影响较大.小型车从桥下通过时几乎可以不考虑追风效应对人行天桥的影响.

3 结论

文章利用前处理器和FLUENT 6.2软件建立了车辆从人行天桥下通过时流场的二维分析模型，通过对人行天桥进行受力分析和周围流场的速度矢量分析，得出了在无风条件下人行天桥受到过往车辆产生的追风效应的原理，并且指出，人行天桥两侧气流速度的不同，以及受到具有脉动性质的瞬时荷载，是产生追风效应的主要原因.在此基础上，分析了不同车速、不同车型的追风效应对人行天桥的影响程度，得出车速对人行天桥的追风效应影响较大，而小型车几乎可以不考虑追风效应影响的结论.