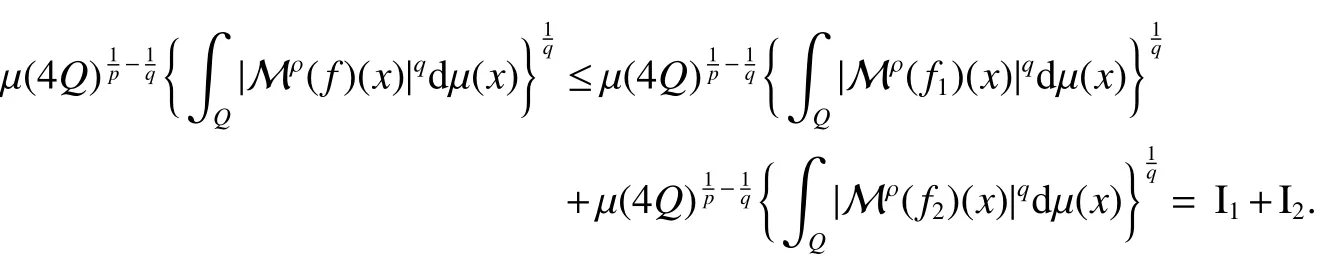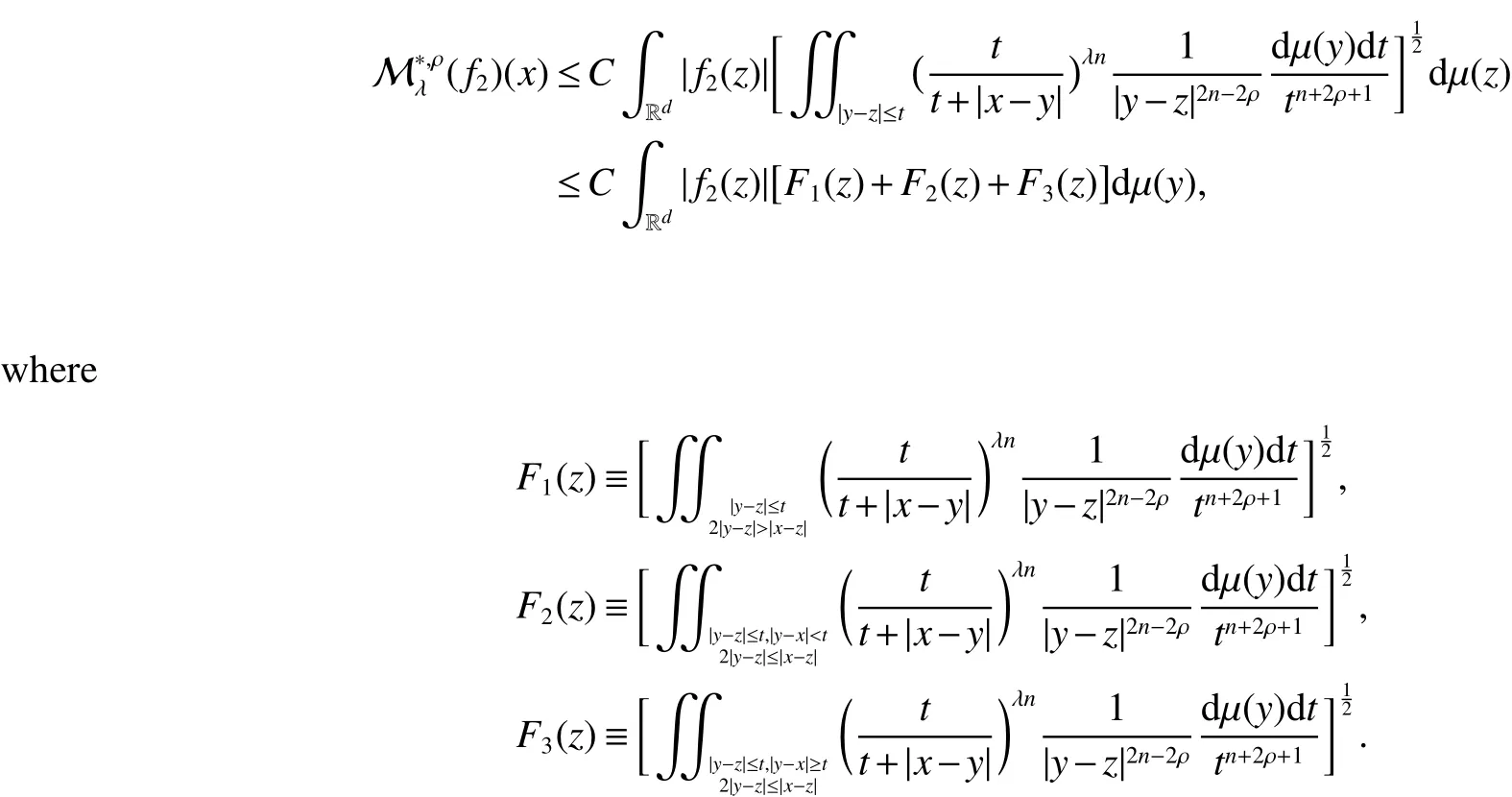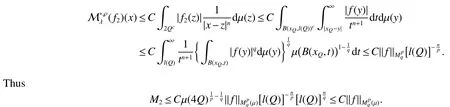Boundedness of Parametrized Littlewood-Paley Operators with Non-doubling Measures on Morrey Spaces∗
LI Tie,JIANG Yin-sheng,ZHOU Jiang
(College of Mathematics and System Sciences,Xinjiang University,Urumqi,Xinjiang 830046,China)
Abstract: Letµbe a non-negative Radon measure on Rdwhich only satis fies the following growth condition that there exists a positive constant C such thatµ(B(x,r))≤Crnfor all x∈Rd,r>0 and some fixed n∈(0,d].We will prove that for suitable indexes ρ and λ the parametrized functionand Mρare bounded on(k,µ)spaces.
Keywords:Non-doubling measures, Morrey space, Parametrized Littlewood-Paley Operators, Parametrized Marcinkiewiczintegral
0 Introduction
Letµbe a nonnegative Radon measure on Rdwhich only satis fies the following growth condition that for allx∈Rdand allr>0,

whereC0andnare positive constants andn∈(0,d],andB(x,r)is the open ball centered atxand having radiusr.Such a measureµmay be non-doubling.We recall thatµis said to be a doubling measure,if there is a positive constantCsuch that for anyx∈supp(µ)andr>0,µ(B(x,2r))≤Cµ(B(x,r)),and that the doubling condition is a key assumption in the classical theory of harmonic analysis.In recent years,many classical results concerning the theory of Calder´on-Zygmund operators and function spaces have been proved still valid if the Lebesgue measure is substituted by a measureµas in(1),for example,see[1,2].
LetKbeµ-locally integrable function on Rd×Rd{(x,y):x=y}.Assume that there exists a positive constantCsuch that for anyx,y∈Rdwithx,y,

and for anyx,y,y0∈Rd,

The parametrized Marcinkiewicz integral Mρ(f)associated to the above kernelKand the measureµas in(1)is de fined by

where ρ ∈ (0,∞).For anyx∈ Rd,the parametrized area integralandfunctionare de fined respectively by
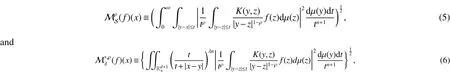

with Ω homogeneous of degree zero and ω ∈Lipα(Sd−1)for some α ∈ (0,1],thenKsatis fies(2)and(3).Under these condtions,Mρin(4)is just the parametrized Marcinkiewicz integral introduced by Ho¨rmander in[3],andandas in(5)and(6),respectively,are the parametrized area integral and the parametrizedfunction considered by Sakamoto and Yabuta in[4].When ρ =1,the operatorMρas(4)is just the Marcinkiewicz integral with non-doubling measures in[5],where the boundedness of such operator in Lebesgue spaces and Hardy spaces was established under the assumption that Mρis bounded onL2(µ).There are some results about the boundedness of M,Mρandwith non-doubling Measures onLp(µ)spaces.In 2007,the boundedness of Marcinkiewicz integral M with non-doubling measures was established onLp(µ)spaces by Hu,Lin and Yang in[5].In 2008,Lin and Meng in[6]proved that the boundedness of parametrized Marcinkiewicz integral Mρandfunctionwith non-doubling measures onLp(µ)spaces.In 2010,the boundedness of Marcinkiewicz integral M with non-doubling measures was established on Morrey spacesby Zhang and Li in[7].
Throughout this paper,we always assume that the parametrized Marcinkiewicz integral with non-doubling measures Mρas in(4)is bounded onL2(µ).The main purpose of this paper is to establish that for suitable indexes ρ and λ the parametrizedfunctionand Mρare bounded on(k,µ)spaces.
To state our results,we still recall some notations and de finitions.The Morrey spaces were introduced by Sawano and Tanaka in[8].
De finition 1Letk>1 and 1≤q≤p<∞.We recall the Morrey spaceMpq(k,µ)as

It is easy to observe thatLp(µ)=(k,µ),and Ho¨lder’s inequality tells usfor all 1≤q2≤q1≤p,then we haveLp=(k,µ)⊂(k,µ)⊂k,µ).The space,µ)is a Banach space with its norm(7)and the parameterk>1 appearing in the de finition does not a ffect it.
Our main theorems are formulated as follows.
Theorem 1LetKbe aµ-locally integrable function on Rd×Rd{(x,y):x=y}satisfying(2)and(3),and Mρbe as in(4)with ρ∈).Then,fork>1 and 1 To state our next theorems,we need a stronger condition for the kernelK,for some fixed σ>2, Theorem 2LetKbe a µ-locally integrable function on Rd×Rd{(x,y):x=y}satisfying(2)and(8),andbe as in(6)with ρ ∈).Then fork>1,λ>2 and 1 Note that for any ρ∈(0,∞),λ∈(1,∞),andx∈Rd, The above inequality together with Theorem 2 deduce that the following theorem. Theorem 3LetKbe a µ-locally integrable function on Rd×Rd{(x,y):x=y}satisfying(2)and(8),andbe as in(6)with ρ ∈).Then,fork>1 and 1 For a cubeQ⊂Rd,we mean a closed cube whose sides parallel to the coordinate axes and we denote its side length byl(Q)and its center byxQ.In what follows,Cdenotes a positive constant that is independent of main parameters involved but whose value may differ from line to line.For a µ-measurable setE,χEdenotes its characteristic function.For anyp∈[1,∞],we denote byp0its conjugate index, Before proving our theorems we introduce two lemmas which will be used on later. Lemma 1[6]LetKbe aµ-locally integrable function on Rd×Rd{(x,y):x=y}satisfying(2)and(3),and Mρbe as in(4)with ρ ∈).Then,for anyp∈ (1,∞),Mρis bounded onLp(µ).That is, Lemma 2[6]LetKbe a µ-locally integrable function on Rd×Rd{(x,y):x=y}satisfying(2),(8)andbe as in(6)with ρ ∈).Then,for anyp∈(1,∞),is bounded onLp(µ).That is, Proof of Theorem 1For anyf∈(µ),and fixedQ,we setf1(x)=fχ2Q(x)andf2(x)=f(x)−f1(x).Then From Lemma 1,we can deduce that As forI2,note that for anyx∈Q,y∈(2Q)c,|x−y|∼|xQ−y|.Applying the Minkowiski inequality and(2)we obtain that Thus The estimates forI1andI2give thatand then the proof of Theorem 1 is completed. Proof of Theorem 2We still adapt the notation in the proof of Theorem 1 and obtain that From Lemma 2,it follows that As forM2,note that for anyx∈Q,z∈(2Q)c,|x−z|∼|xQ−z|,and by(2),we have that Applying the Minkowski inequality and condition(2),it leads to that for anyz∈Rd2Qandx∈Q, As forF2(z),notice that for anyx,y,z∈Rdsatisfying|y−x| To estimateF3(z),we first have that for anyx,y,z∈Rdsatisfying 2|y−z|≤|x−z|,|x−z|≤2|y−x|,then|y−x|≤3|x−z|/2.Choose 0< δandx∈Q,we have Combining the estimates forF1(z),F2(z)andF3(z),we obtain that for anyz∈Rd2Q,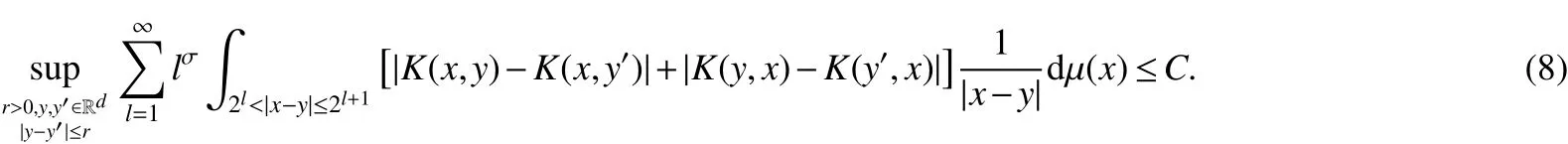
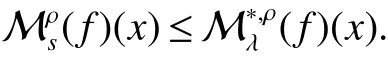
1 Proof of main result