具非线性扩散系数的偶数阶中立型偏泛函微分方程的振动性

林文贤

具非线性扩散系数的偶数阶中立型偏泛函微分方程的振动性

林文贤

(韩山师范学院数学与统计学系，广东，潮州 521041)

本文研究了一类具非线性扩散系数的偶数阶中立型偏泛函微分方程的振动性，借助广义Riccati变换和微分不等式技巧，获得了这类方程分别在Robin, Dirichlet边值条件下所有解振动的若干新的充分性条件，所得结果推广了最近文献的相关结果。

偶数阶；偏泛函微分方程；振动性；非线性扩散系数

近年来，国内外许多学者研究了双曲型偏微分方程解的振动性，已有很多研究成果[1-12]，但对于具有非线性扩散系数的高阶偏微分方程振动性研究的论文则较少[13-15]。本文将研究如下具有非线性扩散系数的偶数阶中立型偏泛函微分方程

分别在边值条件

当=2时，方程(E)是文献[3]所研究的方程，因而本文的结论推广和包含了文献[3]的结果。

假设下列条件(H)成立:

1 主要结果

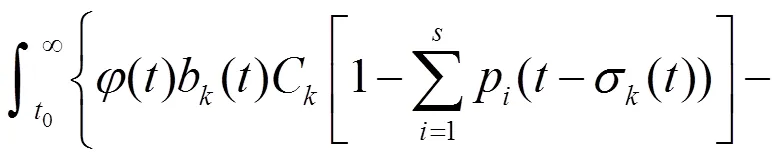
则边值问题(E)，(B1) 的所有解在Ｇ上振动。

由Green 公式和边值条件(B1)及（H3）得

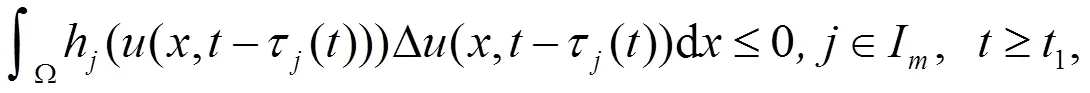
又根据（H1），（H3）有

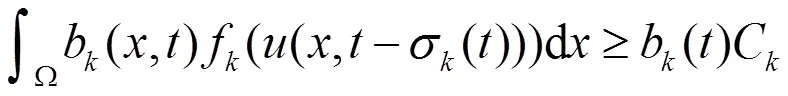
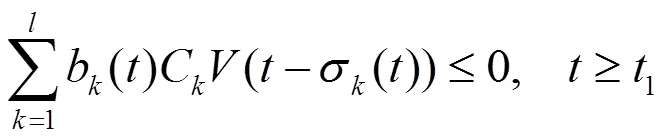
又由（6）式有

从而有

进而得到

注意到(7)、（8）及(H2), 由(10)得

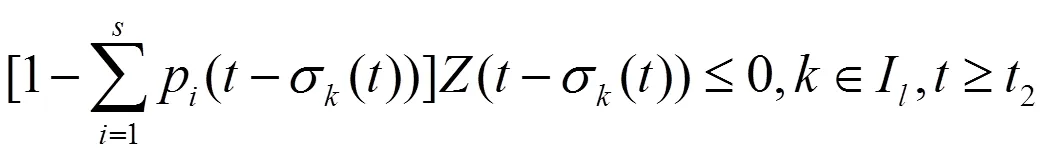
于是由引理2，有

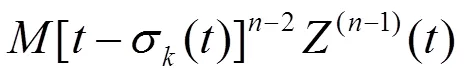
于是由（11），（12）式有

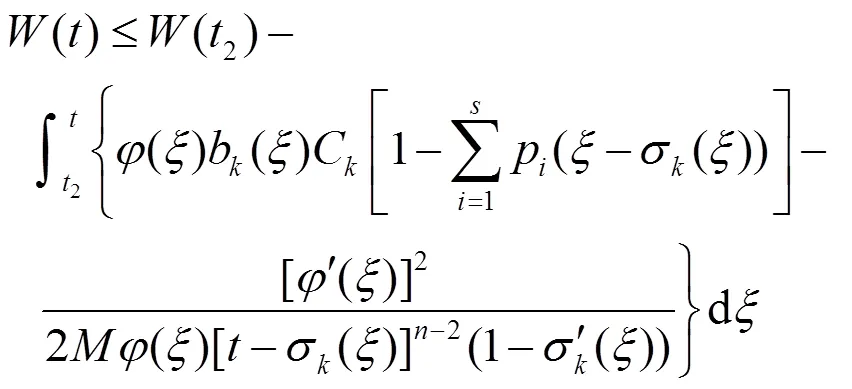
推论1 若将条件(1)换成微分不等式(9)无最终正解，则边值问题(E), (B1) 的所有解在Ｇ上振动。

定理2 若将条件（1）换为

成立，则定理1的结论仍然成立。

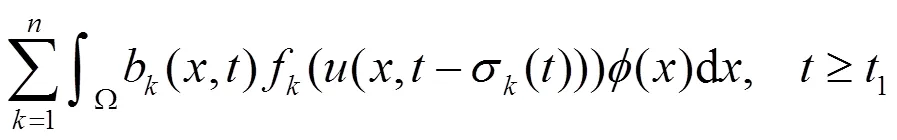
由Green 公式和边值条件(B2)有

又由(H1)和(H2)有

因此得

从而有

进而，有

余下的证明类似于定理1的后半部分的证明，故省略。证毕。

由微分不等式(18)有

类似于定理1的证明，可得如下结果。

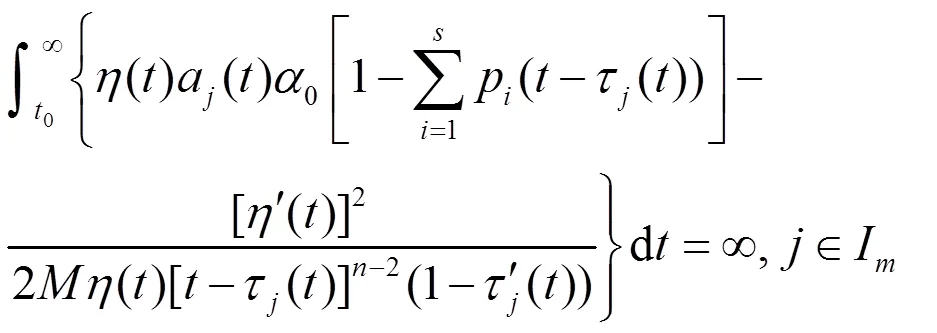
则边值问题 (E), (B2) 的所有解在Ｇ上振动。

[1] Lin Shizhong, Zhou Zhengxin, Yu Yuanhong. Oscillation criteria for a class of Hyperbolic differential equations continuous distributed deviating arguments[J]. J. of Math. (PRC), 2005,25 (5): 521-526.

[2] 王培光，葛渭高.一类非线性偏泛函微分方程的强迫振动性[J].系统科学与数学,2000,20(4):454-461.

[3] 罗李平. 非线性中立双曲型偏泛函微分方程的振动性定理[J].数学杂志,2010,30(6):1023-1028.

[4] 何猛省,高述春.双曲时滞偏微分方程解的振动性质[J]. 科学通报, 1992, 37 (13): 1163-1166.

[5] 林文贤. 一类非线性中立型双曲方程的强迫振动性[J]. 韩山师范学院学报, 2002, 23 (2): 11-18.

[6] 林文贤.一类二阶中立型偏泛函微分方程的振动性[J].数学的实践与认识，2007, 37(20)：192-195.

[7] 林文贤.一类具连续偏差变元二阶中立型偏泛函微分方程的振动性[J]. 韩山师范学院学报, 2007, 28 (3): 8-10.

[8] 林文贤.一类中立型双曲微分方程的振动性定理[J].应用数学,2009, 22(3):514-519.

[9] 林文贤.一类非线性中立双曲型偏泛函微分方程的振动性[J].安徽大学学报:自然科学版,2011, 35(3)：9-13.

[10] 林文贤.一类具分布式偏差变元中立双曲型偏泛函微分方程的振动性[J].南京师范大学报:自然科学版,2011, 34(4):13-16.

[11] 林文贤.一类具连续偏差变元的非线性中立双曲型偏泛函微分方程的振动性[J].昆明理工大学学报:自然科学版,2012, 37(1):90-94.

[12] 林文贤.一类具分布时滞的中立型双曲方程的振动性[J].安徽大学学报:自然科学版,2013, 37(6):8-12.

[13] 林文贤.一类高阶中立型偏微分方程的振动性[J]. 西南师范大学学报, 1998, 23(1):25-30.

[14] 林文贤.高阶非线性中立型偏微分方程的振动性[J].生物数学学报,2003,18(1):8-14.

[15] 林文贤.一类高阶中立型偏泛函微分方程的振动性[J]. 黑龙江大学自然科学学报, 2006, 23(4):449-456.

[16] Agarwal R P, Grace S R, Regan D O. Oscillation Theory for Differential Equations[M]. Kluwer Academic, Dordrecht,2000.

[17] Philos Ch G. A new criterion for the oscillation and asymptotic behavior of delay differential equations[J]. Bull.Acad.Pol.Sci.Ser.Sci.Mat, 1981, 39(1):61-64.

[18] Vladimirov V S. Equations of Mathematical Physics[M]. Moscow: Nauka,1981.

Oscillation of Certain Even Order Neutral Partial Functional Differential Equations with Nonlinear Diffusion Coefficients

LIN Wen-xian

(Department of Mathematics and Statistics, Hanshan Normal University, Chaozhou, Guangdong 521041, China)

The oscillation of a class of nonlinear even orders neutral partial functional differential equations with nonlinear diffusion coefficients are studied. By employing the generalized Riccati transformation and the technique of differential inequalities, some new sufficient conditions for oscillation of all solutions of such equations are obtained under Robin and Dirichlet boundary value conditions. The results generalize some the recent results.

even order; partial functional differential equation; oscillation; nonlinear diffusion coefficients

O175.1

A

10.3969/j.issn.1674-8085.2014.04.004

1674-8085(2014)04-0018-05

2014-04-09；

2014-05-11

广东省自然科学基金项目（S2013010013372）

林文贤(1966-)，男，广东潮州人，教授，主要从事泛函微分方程理论及应用的研究(E-mail:linwx66@163.com).