面向多声道三维音频的和差压缩编码技术

董石，胡瑞敏，杨玉红，王晓晨，涂卫平

(武汉大学 国家多媒体软件工程技术研究中心，湖北 武汉 430079)

1 引言

随着三维影视市场的巨大成功，三维音频技术受到了广泛关注并得到了迅速发展。三维音频系统因其能为观众提供更好的声音定位和临场感，越来越多被引入与音频相关的应用当中取代传统环绕声系统。波场合成(WFS,wave field synthesis)、Ambisonics和幅度矢量合成(VBAP,vector based amplitude panning)是目前发展最为完备的3种多声道三维音频理论，其中WFS基于惠更斯原理重建原始声场信号，德国Fraunhofer研究院的IDMT实验室和法国 IRCAM 等研究机构都开展了长期研究，并尝试将 WFS应用于剧场和音乐会的实时直播；Ambisonics利用球谐函数记录声场并驱动扬声器。其有严格的扬声器排布要求，能够在扬声器中心位置高质量重建原始声场；VBAP基于三维空间中的正弦法则，利用空间中3个临近的扬声器形成三维声音矢量。由于算法简单，VBAP也是最常用的多声道三维音频技术[1]。如日本NHK公司的22.2多声道三维音频系统正是利用VBAP技术进行三维声像的生成，2012年面向三维音频的国际标准MPEG-H正在制定当中，22.2多声道三维音频系统也被其作为标准系统。

未来三维音频技术将逐渐走向成熟并取代现有的立体声和环绕声技术。当前三维音频系统的一个主要特点就是其庞大的声道数目。例如 WFS一般包含了数十个甚至上百个声道，22.2多声道系统也有分3层排布的24个声道，而Ambisonics系统虽然可以灵活地制定声道数目，但由于较少的声道数会严重影响三维音质，因此声道数一般也有几十个。相比于双声道立体声和5.1环绕声技术，三维音频技术中声道数的增加带来了数据量的激增。来自Fraunhofer的研究报告显示，WFS用于实时传输时需要高达37 Mbit/s的码率；而对于未压缩的22.2多声道系统也需要28 Mbit/s的码率[2]。2011年，殷福亮等对三维音频技术进行了综述，指出三维音频巨大计算量和数据量是其发展的瓶颈问题[3]。目前的存储介质和传输带宽难以满足三维音频庞大数据量的需求，因此三维音频信号的压缩技术将成为三维音频领域的重要研究方向。

针对三维音频数据量激增的问题，近期在三维音频压缩方面已经展开了一些非常有价值的工作。2007年，Goodwin等提出了一种基于主成分分析的参数编码多声道压缩框架[4]，这种框架可以应用于增强特殊的音频场景信号并提高空间音频编码的顽健性。2008年，Cheng提出了一种空间压缩环绕声编码(S3AC)方法，用于Ambisonics信号的参数编码[5]。2009年，Hellerud使用声道间预测编码的方法去除Ambisonics声道间的冗余信息[6]，这种方法具有较低的算法延时，但是计算复杂度较高。2010年，Pinto利用时空域变换将WFS信号分解成平面波和瞬态波，通过舍弃瞬态波，并利用感知编码对平面波信号进行压缩，来获得编码增益。由于其时空变换的精度取决于空间分辨率，也即 WFS声道数目，所以编码效率会随着单位空间内声道数的增加而提高[7,8]。2011年，Cheng又进一步提出了一种空间定位量化格点(SLQP,spatial localization quantization point)的参数编码方法，并使用三维方位线索来压缩VBAP信号[9]。由于提取了空间线索并通过下混技术减少了声道数目，SLQP取得了较高的压缩效率。

上述模型和参数编码方法可以提供较高的压缩比，但实际应用中音频编码器要兼顾算法复杂度和编码效率2个方面，而且参数编码也只能在低码率下提高编码音质。所以本文考虑高质量/高比特率的应用情况，并专注于传统和差编码方法(M/S,mid/side coding)。本文提出一种基于三声道的M/S编码方法(3D-M/S,three-channel dependent mid/side coding)和相应框架，用于压缩VBAP三维音频系统和 22.2多声道系统的音频信号。首先分析了传统M/S编码技术的基本原理，并基于传统方法原理提出新的变换矩阵，将传统M/S编码方法拓展到三维空间情况，实现三维空间中基本单元——三声道的信号冗余去除。进一步，提出一种基于三声道组的三维音频编解码框架，使3D-M/S能够压缩任意声道配置。最后，将所提算法和独立声道编码(independent channel coding)、PCA 编码(PCA,principal component analysis)在算法复杂度和客观质量上进行了对比，实验表明3D-M/S方法保留了传统M/S编码低复杂度、高效率的特点，适用于三维音频直播通信传输的需求。

2 三维空间中和差编码

2.1 传统立体声M/S编码

由J D Johnston提出的M/S编码技术[10]被多种主流音频压缩标准采用，如 MPEG1-Audio Layer 3(MP3)和aacPlus (AAC+)。M/S编码基于“立体声2个声道是强相关信号”的现象，不直接编码原始双声道信号，而利用M/S变换将原始声道转换为和声道与差声道进行编码。由于差声道信号动态范围小于原始信号，编码所需的比特数更少，因而获得编码增益。

本文通过立体声正弦模型来说明 M/S的编码过程，首先用矢量 V0=(CL,CR)来表示立体声道信号

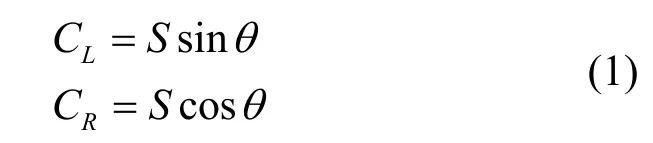
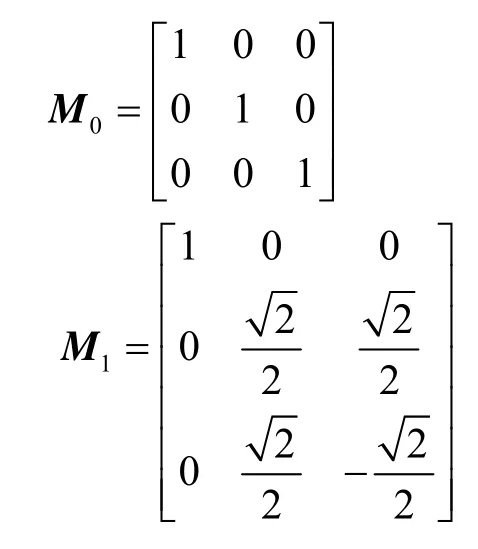
其中，S为虚拟声源信号，θ为音源的方位角，代表音源能量分布于在2个声道的增益因子，且θ∈[0,π/2]。M/S编码的2个变换矩阵M0和M1为

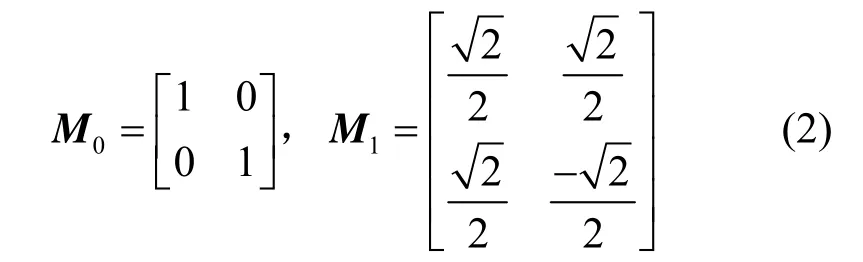
实际编码时CL和CR为子带的能量值。当2个声道信号差异较大时，和差变换后差信号的能量依然较大，M/S编码使用矩阵M0编码原始信号；当2个声道非常相似时才会使用M/S编码，因为变换为和差信号后会重新计算掩蔽阈值，增加编码复杂度。如MP3标准中2个声道信号满足能量判别条件（3），即当能量差异小于阈值Thr=2 dB时，才使用矩阵M1编码进行和差变换[10]。

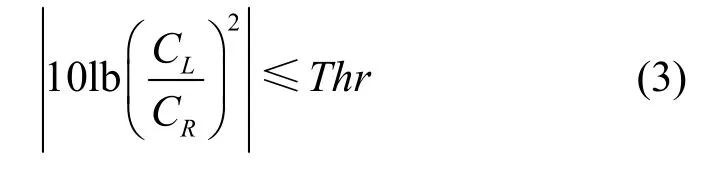
为了方便讨论矩阵切换，这里将判别条件表示为2个向量的距离。将 CL/CR=tan θ代入式(3)可得到

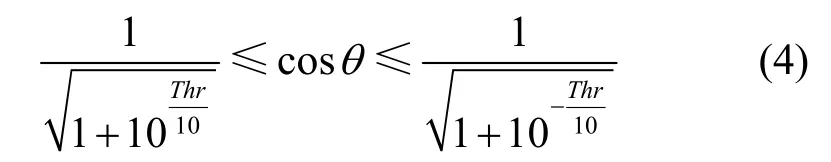
此处的Thrv是能量阈值Thr对应的矢量距离阈值

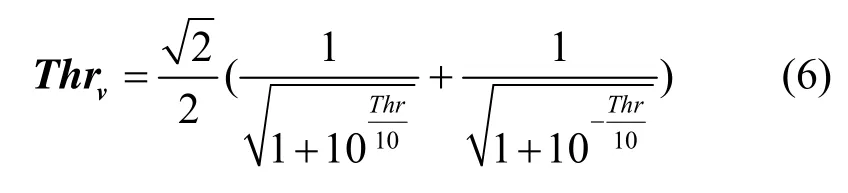
式(5)即为能量判别条件的等价矢量表示，其表明只有输入信号矢量V0与变换矩阵 M1的和矢量V1足够接近时才使用和差变换矩阵。这个矢量表示对下节讨论三维空间M/S编码将会十分有用，因为三维空间M/S编码存在多于一个的变换矩阵及其和矢量。

2.2 三维音频M/S编码

传统立体声和环绕声系统中为了保证声像的稳定性，只用最邻近的2个声道形成一个有方向的声像，所以2个邻近的声道具有最大相似性，因而M/S编码和其他参数编码也是基于 2个声道单元去除冗余。

对于Ambisonics和VBAP等三维音频系统（如图 1所示），其声道在三维空间中的球面上排布，具有三维特性，与立体声和环绕声有很大差异。首先，在球面排列的三维音频系统中，三角形是能覆盖三维空间中区域的最小组合，因此最少要使用 3个声道才能在三维空间某一区域内的任意位置形成声像。其次，VBAP算法只用邻近3个声道(C1,C2,C3)形成一个虚拟声像，这 3个声道之间具有最大相关性。基于三维音频的这种特点，本文提出一种基于三声道的和差编码算法（3D-M/S）编码球面排布三维音频信号。

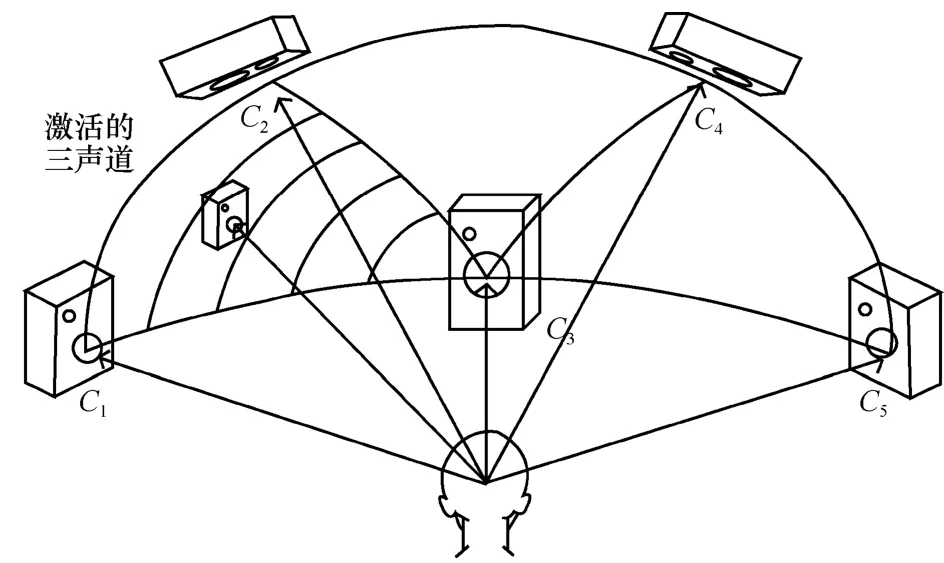
图1 VBAP系统在三维空间球面上的扬声器排布

此处按照传统 M/S编码算法对三声道情况进行讨论，基于三维空间中正弦模型，VBAP三维音频系统信号可表示为矢量 V0=(C1,C2,C3)，其中

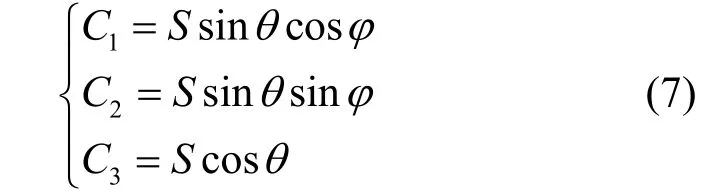
且θ,φ∈[0,π/2]，它们确定了 3个声道的增益因子和声像位置。声像位置可分为3种基本情况。第 1种情况，只通过一个声道产生声像，对应于声像正好定位于在某一个声道所在位置，即球面三角形的顶点，此时和立体声中仅使用一个声道的情况相同，3个声道信号完全不同，因此使用M0矩阵编码原始声道。第2种情况，只通过2个声道产生声像，此时对应于虚拟声源位于 2个声道之间，即球面三角形的边上。这种情况和传统的立体声相同，因此使用 M1矩阵编码。但由于三声道中有种两声道情况，M1变换矩阵需要相应的拓展成3种变换矩阵，拓展方式如(8)中M1，M2和 M3所示遍历所有种两声道情况。第3种情况，3个声道都用于产生声像。此时对应于虚拟声源位于 3个声道之间，即球面三角里面。为了实现这种情况下声道间冗余信息去除，需要依据传统M/S编码原理设计新的变换矩阵M4。其第一个矢量是和矢量，其余矢量与和矢量正交且相互正交，保证其余2个声道将变换为差声道。

3D-M/S编码的矩阵判别条件和传统M/S编码采用相同的方法设计：当3个声道中有且仅有2个声道满足传统M/S编码切换条件时，选择M1，M2，M3中和矢量与输入矢量距离最近的矩阵，得到一个能量较小的差声道；当3个声道中所有声道之间均满足传统M/S编码切换条件时，表明3个声道差异很小。此时采用变换矩阵 M4，得到 2个能量较小的差声道。利用矢量距离的方式，上述3D-M/S编码切换条件可以表示为

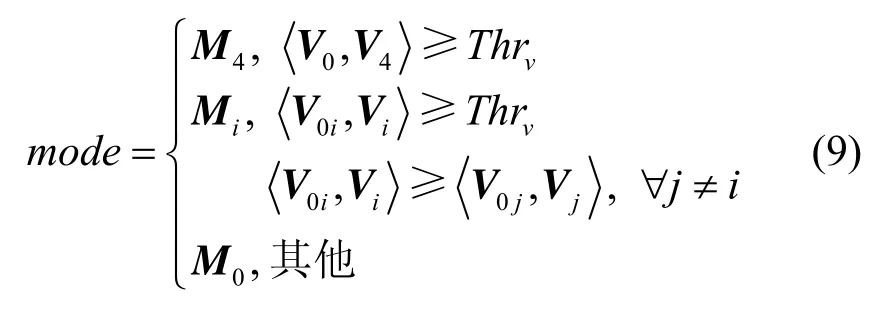
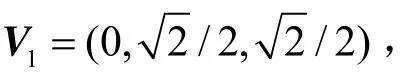
3 基于3D-M/S的多声道编码框架

3D-M/S编码只适用于三声道情况，实际三维音频系统都包含更多声道数目。球面排布三维音频系统的多声道配置可归纳为图2所示的拓扑结构，每一个声道Ci对应一个扬声器。

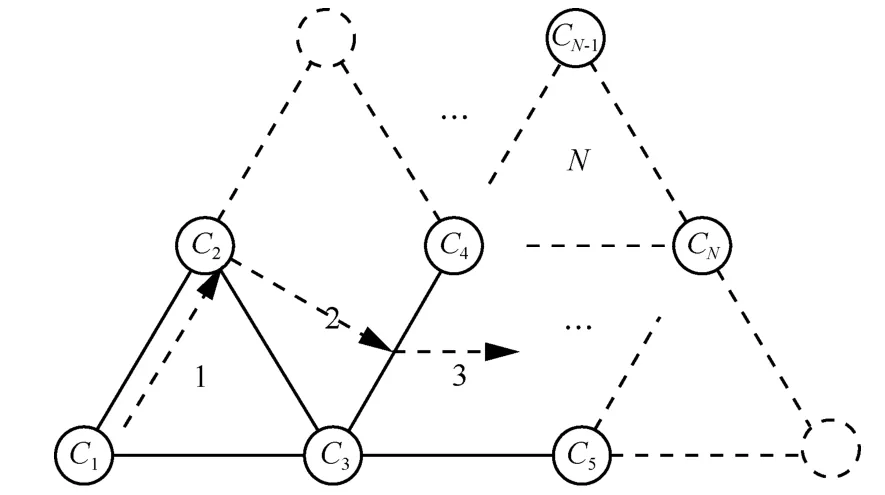
图2 三维音频系统中多声道排布的一般情况

为了让3D-M/S编码能够去除多声道信号冗余，本文提出一种三维音频编码框架如图3所示，其中CM为和声道，CS和CT分别是第2个和第3个差声道。该框架对拓扑结构中声道按三角形逐个处理，直到所有的声道都被编码完为止。每个3D-M/S编码单元和前一个单元共用 2个声道，即每个单元只加入一个新的声道。除第一个编码单元外，其他单元只将3D-M/S变换后第3个差声道CT送入核心编码器，保证了编码声道数和原始输入声道数完全一致。由于 3D-M/S变换矩阵均为正交矩阵，在解码端3D-M/S解码单元通过解码出的声道CT和前一单元的 2个声道，可以还原出原始声道信号。当变换矩阵为M0时，CT为原始声道，当变换矩阵为M1、M2、M3、M4时，CT为差声道，与编码原始声道相比，整个框架通过编码差声道获得编码增益。

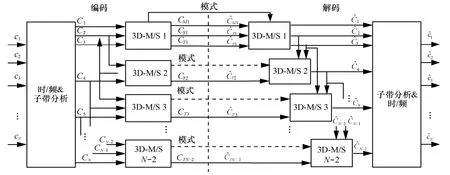
图3 针对多声道的3D-M/S编解码框架

4 实验与性能分析

4.1 实验配置

PCA是理论上最好的去相关变换算法，因此本文选取了3D-M/S、PCA和独立声道编码3种编码方法，分别在比特率、复杂度、客观音质上进行对比。复杂度通过各编码器在PC(CPU: Intel Core2 Duo P86002.53 GHz,RAM:8 GB)上的运行时间来衡量；客观音质则使用分帧信噪比和ITU标准推荐的客观质量ODG评分来衡量[11]。实验采用图2所示的五声道配置(C1,C2,C3,C4,C5)。测试所用的三维音频信号为合成的 VBAP信号，该信号使用 3个MPEG测试序列(es01语音，sc03交响乐，si02响板，48 kHz采样)作为虚拟音源，虚拟声源的定位依据VBAP算法实现。由于实验中无法涵盖虚拟声源的所有可能位置，因此实验采用空间中3种代表性的声源位置：声源在三角形中从一个顶点移动到另一个顶点，从一个顶点移动到对边，以及从一条边移动到另一条边，如图2箭头方向所示。

本文算法基于开源AAC编码器FAAC-1.28实现，解码器基于对应的 FAAD2-2.7实现。与传统M/S编码相同，编码器在频域上按个子带进行3D-M/S和PCA编码。为了便于码率分析和算法实现，核心编码器关闭了长短窗切换，只采用固定的长窗。这会同等程度降低各种对比算法的信噪比，但结果不失一般性；为了避免FAAC动态带宽设置功能带来的影响，实验中采用固定编码带宽12 kHz和35个均匀子带。

独立声道编码：声道送入核心编码器单独编码。

3D-M/S编码器：通过原AAC编码器已有的子带能量进行矩阵判别并进行矩阵变换，一个子带的变换矩阵索引使用3 bit来量化。

PCA编码器：计算每个编码单元信号的特征向量，并通过特征向量将三声道子带转化为去相关后的主要成分和次要成分，然后送入核心编码器。遵循已有PCA多声道编码算法[12]，每个子带用24 bit量化协方差矩阵，最后传递到解码端重建特征向量并将主次成分还原为原始声道。

4.2 客观质量测试和复杂度测试

图4显示了3种编码方法对声像移动的声道编码后的分帧信噪比值。声源1 位置移动的时间范围从1～400帧，声源2位置移动的时间范围从400～800帧，声源3位置移动的时间范围从800帧到最后一帧。首先，图中所有的信噪比曲线都呈下降趋势，这是因为瞬态信号和交响乐具有更加丰富的信息频谱细节，使得它们更难被压缩。其次，当虚拟声源位置接近 2个声道间时(200帧 C1、C2之间，400～800帧C4、C5之间)，3D-M/S比声道独立编码的方法具有更高的信噪比。特别是在接近600帧时，3个声道几乎完全相同，此时通过变换矩阵M4可以最大程度地去除冗余，2个差声道能量几乎为零。可以保留更多比特数编码和声道，因此此时3D-M/S的效果优于PCA方法。

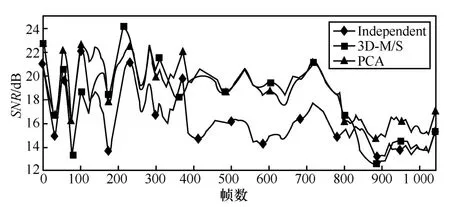
图4 3种方法在虚拟音源位置移动下的分帧信噪比

表1显示每种方法所用的比特数和复杂度。3种方法采用大致相同的码率进行编码以进行对比，ODG分数由整个信号计算所得。数据表明PCA和3D-M/S都获得了约0.66 ODG分的改善，但是PCA算法涉及协方差矩阵计算，复杂度提高了 29.9%。而3D-M/S只进行矩阵变换，所以复杂度仅提高了11.3%，是PCA方法的37.8%。并且PCA的参数码率为每声道 39.3 kbit/s远高于3D-M/S每声道的4.9 kbit/s。这种高参数码率在3个声道不相关(比如声道记录不同内容，声道间信号冗余非常小)情况下，核心编码器无法获得编码增益，高参数码率反而导致编码效率下降。但3D-M/S参数码率仅为每声道4.9 kbit/s，在其主要应用场景的高码率下，其编码效率不会明显降低。

表1 3种方法的ODG质量、比特率、时间复杂度

5 结束语

本文针对多声道三维音频系统提出了一种拓展和差编码技术，将传统基于声道对的M/S编码方法拓展为基于三声道的3D-M/S编码，并继承了传统 M/S编码低复杂度的特点。对于 VBAP和Ambisonics等球面排列的三维音频系统，空间中三声道是形成声像和冗余存在的最小单元，因此3D-M/S更符合三维音频的空间结构。结合所提编码框架，3D-M/S可以进一步对3个声道以上的三维音频系统进行压缩编码。实验表明，与 PCA编码和独立编码相比，3D-M/S在保持较低复杂度的同时提供了相当的压缩效率。考虑到三维音频技术的快速发展及其直播通信中终端处理能力，在实际应用中低复杂度的音频编码技术会更有应用前景。

[1]COOPERSTOCK J R. Multimodal telepresence systems[J]. IEEE Signal Processing Magazine,2011,28(1):77-86.

[2]SAKAIDA S,IGUCHI K,NAKAJIMA N,et al. The super hi-vision codec[A]. IEEE International Conference on Image Processing[C].San Antonio,TX,2007.21-24.

[3]YIN F,WANG L,CHEN Z. Review on 3D audio technology[J]. Journal on Communications,2011,32(2):130-138.

[4]GOODWIN M M,JOT J. Primary-ambient signal decomposition and vector-based localization for spatial audio coding and enhancement[A]. IEEE International Conference on Acoustics,Speech and Signal Processing[C]. Honolulu,HI,2007.9-12.

[5]CHENG B,RITZ C,BURNETT I. A spatial squeezing approach to ambisonic audio compression[A]. IEEE International Conference on Acoustics,Speech and Signal Processing[C]. Las Vegas,NV,2008.369-372.

[6]HELLERUD E,SOLVANG A,SVENSSON U P. Spatial redundancy in higher order ambisonics and its use for low delay lossless compression[A]. IEEE International Conference on Acoustics,Speech and Signal Processing[C]. Taipei,China,2009.269-272.

[7]PINTO F,VETTERLI M. Wave field coding in the spacetime frequency domain[A]. IEEE International Conference on Acoustics,Speech and Signal Processing[C]. Las Vegas,NV,2008.365-368.

[8]PINTO F.,VETTERLI M. Space-time-frequency processing of acoustic wave fields: theory,algorithms,and applications[J]. Signal Pro-cessing,IEEE Transactions on,2010,58(9): 4608-4620.

[9]CHENG B,Spatial Squeezing Techniques for Low Bit-Rate Multichannel Audio Coding[D]. University of Wollongong,2011.

[10]JOHNSTON J,FERREIRA A J. Sum-difference stereo transform coding[A]. IEEE International Conference on Acoustics,Speech and Signal Processing[C]. San Francisco,CA,1992.569-572.

[11]ITU-R. BS Recommendation 1387-1.Method for Objective Measurements of Perceived Audio Quality[S]. 1998.

[12]DAI Y,HONGMEI A,KYRIAKAKIS C,et al. High-fidelity multichannel audio coding with Karhunen-Loevetransform[J]. IEEE Transactions on Speech and Audio Processing,2003,11(4):365-380.