平面二维水沙数学模型在灞河橡胶坝库区的初步应用
刘 洋
(江西省水利规划设计院 江西 南昌 330029)
1 概述
对于河流的泥沙问题,目前采用较多的研究方法主要有物理模型试验和数值模拟两类。物理模型具有直观、可重现历史状况、可进行未来问题预测等优点,但其实验周期长、费用高,且受比尺及实验环境、场地的影响大。自二十世纪五十年代以来,随着计算机的出现和现代高速计算机技术的快速发展,数学模型在水利工程的许多领域已得到广泛应用,而计算水力学理论的成熟又促进了求解流体力学方程方法的发展,使流动现象的数值模拟达到了更高的水平。数学模型以计算水力学、河流动力学与环境水力学等学科为基础,将现代计算机与数值解技术相结合对河流进行模拟研究,与物理模型试验相比,具有研究费用较低、周期短、运用灵活、不存在比尺效应和试验环境影响等显著优点,应用数学模型研究河流泥沙问题无疑是该领域研究的发展方向。
水沙数学模型按所模拟的水沙运动在空间上的变化情况可分为一维模型、二维模型和三维模型。到目前为止,一、二维水沙数学模型的研究已相对成熟,三维水沙数学模型的研究尚处于探索阶段。一维水沙数学模型只能求解河道断面各水沙要素沿河道长度方向的平均值,无法回答河段内部沿河宽方向冲淤变化的分布问题,对于很多实际工程问题比如水库坝前泥沙的运动、河床变形分析和过机泥沙预测等是解决不好的,而平面二维水沙数学模型却能较好地解决这些问题,其在水利工程上的应用非常广泛。
2 数学模型的构建
2.1 模型简介
丹麦水力研究所(DanishHydraulic Institute,简称DHI公司)研发的DHI系列模型软件,是目前世界上领先的并经实际工程验证最多的,被水资源研究人员广泛认同和应用的优秀模型软件之一。其涉及范围广泛,从一维模型到三维模型,从单一的水动力模拟到水环境与生态系统相结合的复杂模型。其具有界面友好、模拟计算快速准确、后处理方便等优点。
MIKE21是DHI水动力学模型系统之一,是一种通用的二维数值模拟系统,它可以用来研究河流、湖泊、河口、海湾、海岸及海洋等各类环境下的水流、波浪和泥沙问题。它既可以模拟简单的二维非恒定流,也可以对密度变化、水下地形变化、潮汐变化和降水蒸发等复杂条件下的流动进行分析计算。本文基于MIKE21中的水动力模型和输泥模型构建一个平面二维水沙数学模型。
2.2 基本方程
本文采用的数学模型的基本方程主要包括水动力模型和泥沙模型控制方程两部分。
水动力模型的控制方程为:质量守恒方程:
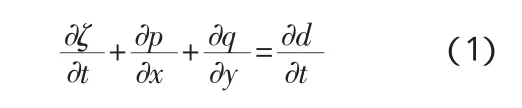
x方向动量方程:
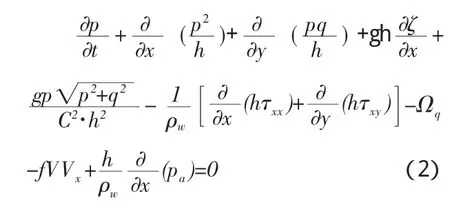
y方向动量方程:
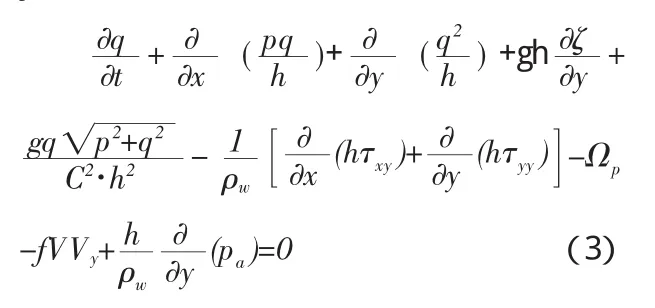
其中:h为水深,m;d为水位随时间的变化量,m;ζ为表面水位,m;p和q分别为x与y方向的通量密度,m3/sm;u和v分别为沿水深的平均流速,m/s;C为谢才系数,m1/2/s;f为风摩擦系数;V、Vx和Vy为风速及其在x与y方向的分量,m/s;Ω为科氏系数,s-1;Pa为大气压,kg/m/s2;ρw为水的密度,kg/m3;t为时间,s;τxx、τxy、τyy为有效切应力分量,N/m2。
该方程的数值解法主要采用交替方向隐式技术(ADI)分别对质量守恒与动量方程进行时空上的积分,根据双扫描法求解每个方向及每个单独的网格产生的方程矩阵。
泥沙模型的计算是基于水动力计算的结果,其控制方程为:

其中:c为垂向平均含沙量,kg/m3;x与y为空间坐标,m;u、v分别为x与y方向的垂向平均流速,m/s;h为水深,m;Dx、Dy分别为x与y方向的泥沙紊动扩散系数,m2/s;QL为水平单位面积源项流量,m3/s/m2;CL为源含沙量,kg/m3;S为冲淤项,kg/m3/s。
该方程为一对流扩散方程,采用以QUICKEST格式为基础的三阶有限差分显式格式(即ULTIMATE格式)求解。该求解格式已经在许多涉及对流扩散方程的紊流模型、环境模型以及其他类似问题中得到了很好的应用。与其他数值解法相比,它具有诸多优越性,尤其避免了与对流项中心差分相关的“蠕动”的不稳定性,同时也在一定程度上减小了一阶迎风格式的数值耗散。

图1 河道淤积厚度分布

图2 各断面淤积厚度历时变化曲线
3 数学模型在灞河橡胶坝库区的应用
3.1 模拟区域概况
灞河属黄河流域,渭河水系,是渭河的一级支流,发源于秦岭北麓蓝田、渭南、华县交界处的蓝田县灞源乡箭峪岭南九道沟,由南向北流,经灞源后西行,到冯家湾出峪口。河流全长104km,流域面积2581km2(含浐河760km2),河床平均比降6.0‰。
灞河流域地形南高北低,属秦岭土石山区,岩石裸露,土层较薄,植被良好,平时水质清澈,洪水时挟带少量泥沙。上游(蓝田故京)平均比降9.0‰,洪水猛涨暴落,水流湍急;中游(故京至浐灞交汇口)河道为平原弯曲型河道,河床断面形态为宽浅式,比降为2.35‰;下游(浐灞交汇口至灞河入渭口)属于平原河道,河床宽浅,比降较缓,为1.58‰。
目前,在灞河中下游修建有大量橡胶坝工程。为了城市防洪和维持水面景观,橡胶坝建成以后长期立坝运行,加之该处河道比降较小、水面宽浅,使得河道水体流动性变差。水土流失问题与上述问题的综合作用使得该处库区泥沙淤积问题非常突出,采用数值模拟的方法对该河段泥沙淤积问题进行研究不失为一种有效的途径。
3.2 模拟计算结果分析
根据实测地形和水文资料,以灞河B号坝库区为例,进行数值模拟计算。模拟的河段长约2.5km,平均比降为2.35‰,河床糙率为0.033。根据实测地形进行非结构网格划分,共划分1016个网格,该河段上游入口宽约356m,下游出口宽度采用的是B号坝的坝长,为450m,立坝运行,在该河段中心处有一河心岛。
采用的水沙过程为枯水期资料,即1955年至1965年灞河逐日水沙过程。模拟总时长为10年,时间步长为50s,对模型参数进行反复调整率定,进行模拟计算后,最后达到冲淤平衡后的河床淤积厚度的分布如图1所示。
从图1中可以看出,随着时间的推移,在该河段上游形成了一狭长的主河槽,主河槽两侧的白色区域为淤积作用造成的露出水面的河滩地,水流主要沿着主河槽绕过中间河心岛向下游流动。主河槽处深色区域明显大于两侧,说明高浓度悬沙在枯水期橡胶坝库区长期立坝造成河道水体流动性变差以后,更容易落淤,最大淤积厚度达到了3.5m以上,该河段在长时间系列中的淤积作用还是相当严重的。
提取模拟所得该河段各断面各时间段淤积厚度数据,绘制淤积厚度历时变化曲线,如图2所示。从图2中可以看出,河床的淤积厚度随着时间的推移逐渐增大,最终于相应的年限达到平衡状态。达到冲淤平衡的时间表现为上游早下游晚,最终的淤积厚度主要分布在3m~3.5m之间。其中,灞4~灞27各断面计算值达到平衡的年限分别为4年、4.5年、4.5年、4.5年、4.5年、5年、5年、6年,其平衡时的淤积厚度值分别为3.00m、3.11m、3.20m、3.32m、3.21m、3.03m、3.41m、3.42m,整个库区的淤死年限为6年。
4 结语
本文首先对水沙数学模型的发展现状进行了简单介绍,然后阐述了所采用的数学模型的控制方程和其数值方法。应用所构建的数学模型在灞河B号橡胶坝库区河段进行了模拟计算,通过分析河道的冲淤演变规律发现,在枯水期橡胶坝库区长期立坝情况下,该河段淤积作用是相当严重的。利用本文所构建的平面二维水沙数学模型可以对河道的冲淤演变趋势进行预测分析,得出河道的演变规律。可见,采用数值模拟方法来研究并处理灞河橡胶坝库区泥沙淤积问题无疑是一种可供参考的有效途径。
[1]李义天,邓金运,孙昭华,等.河流水沙灾害及其防治[M].武汉:武汉大学出版社,2004.
[2]白玉川,杨建民,黄本胜.二维水沙数学模型在复杂河道治理中的应用[J].水利学报,2003,(9):25-30.
[3]孙小军,黄志文,魏炳乾.灞河流域水文分析[J].黑龙江水专学报,2005,(4):40-42.
[4]邵学军,王兴奎.河流动力学概论[M].北京:清华大学出版社,2005:49-148.
——美丽的家园

