裂隙岩体水－岩耦合传热研究

龙 伟 童富果 李 彪

（三峡大学 水利与环境学院，湖北 宜昌 443002）

地下岩体中，尤其是浅层岩体中，存在大量的断层、节理和裂隙.完整岩块的渗透系数相对较小，水在岩体中的运动主要是在裂隙中的流动［1］.裂隙网络构成了地下水的渗流通道，裂隙水的流动会影响岩体的温度场分布.研究裂隙岩体的水－岩耦合传热规律在土木工程、水利水电工程及地热开采［2－4］等诸多领域有着重要应用.

裂隙网络中水的流动会与岩石之间发生对流换热，进而影响裂隙岩体的温度场.单个裂隙是复杂裂隙系统的基本组成单元，对单个裂隙水－岩耦合传热规律的研究是探究复杂裂隙网络传热机理的基础.在简单裂隙水－岩耦合传热方面，国内外学者已做了大量的研究工作.王如宾［5－6］对单个裂隙内水流的稳定温度场进行了理论分析，推导求出了平行板状裂隙稳态温度场的理论公式.路威［7］推导出了单裂隙岩体渗流－传热解析解，计算分析裂隙水及岩体的温度分布特征和参数的敏感度.张树光［8］对单裂隙岩体进行了流－热耦合方面的数值模拟.刘学艳［9］对裂隙岩体水流－传热进行了试验和数值模拟分析，研究了裂隙开度、裂隙流量和热源功率对流场和温度场的影响.白兰兰［10］分析了平板裂隙渗流和圆柱形通道渗漏两种情况下整个裂隙岩体的温度分布特征，讨论了流量、流体与岩体温差等因素对裂隙岩体温度场分布的影响.赵坚［11］通过加热岩石和迫使水流在岩石裂隙的循环，进行了岩石裂隙的水力－热力特性试验研究.徐义洪［12］研究了渗流作用下深部矿场采动区围岩的传热机理.董海洲［13］对岩石单裂隙渗流－传热模型及其参数进行了敏感性分析.基于各自不同的研究目的及需要，上述研究均做了不同程度的假设性规定，存在一定局限性.考虑到水－岩耦合传热的复杂性，有进一步深入研究的必要.

本文基于水－岩耦合传热控制微分方程，采用有限单元法计算分析裂隙水流通过单一裂隙时的温度场.研究主要围绕裂隙宽度、裂隙水流速等因素对水－岩耦合传热的影响开展工作.空间网格离散采用了迎风加权的有限元格式，以消除热传输求解中遇到的数值振荡难题.此外，在涉及水－岩耦合传热的病态方程组数值求解技术方面，本文也做了一定的探讨.

1 数学模型

在传统温度场计算中，通常将流体和固体之间热交换用对流换热来描述，对流换热量采用牛顿冷却定律简化计算.此简化方法虽然可提高计算效率，但终究忽略了流体与固体接触面的真实传热过程，不宜用于水－岩耦合传热规律研究.为满足水－岩耦合传热精确研究的需要，本研究直接基于流－固耦合传热控制微分方程展开.

1.1 水－岩耦合传热控制方程

基于传热学的基本理论，裂隙岩体热传递现象主要包括因温度梯度导致的热传导和因裂隙水流流动引起的热传输，其方程［14］描述为

在一般情况下水、岩的密度ρ，比热c变化很小，可视为常数，进而式（1）简化为

对于固体区域，由于没有流动，可忽略传输项，式（2）可以简化为

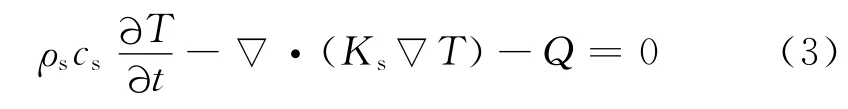
对于流体区域，既要考虑传导，又要考虑传输式（2）可以表示为

其中，ρ是介质（岩石或水）密度（kg／m3）；c是介质比热容（J／（kg·℃））；T 是温度（℃）；K 是导热系数矩阵（J／（m·℃·s））；vw是介质流动速度（m／s）；Q 是热源（J／（s·kg））.

式（2）中的第1项表示热量对时间的变化率，第2项是热传导通量，第3项是热传输量，第4项为热源，由于本研究不涉及产热过程，故此项可忽略.

1.2 几何模型

计算分析对象为包含单一裂隙的矩形区域，模型高H＝32mm，长L＝32mm，裂隙宽度根据计算分析的需要分别设为b＝0.5、1.0、1.5、2.0、2.5mm.对于不同的裂隙宽度，有限元空间网格离散节点数为7 026～13 446个，单元数为6 970～13 370个（如图1所示）.

图1 水－岩耦合传热有限元分析几何模型

1.3 初始及边界条件

岩石及裂隙水流初始温度均为30℃.岩石区域外边界为已知温度边界，其中裂隙左侧入口处水温为20℃，岩石上下边界温度均为30℃，左右边界为绝热边界.

1.4 主要计算参数

裂隙水密度为ρw＝997kg／m3，导热系数λw＝0.6W／（m·℃），比热容cw＝4 190kJ／（kg·℃）；岩石的密度ρs＝2 500kg／m3，导热系数λs＝1.5W／（m·℃），比热容cs＝970kJ·（kg·℃）.鉴于裂隙渗流远远大于岩石本身的渗流，故本研究仅考虑水在裂隙通道内的流动，基于平行板裂隙模型［1］，裂隙水流流速呈抛物线性分布，如图2所示，流速方程为

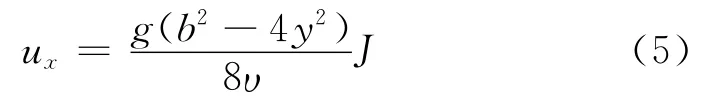
其中，J为水力梯度，υ为水的动力粘滞系数.

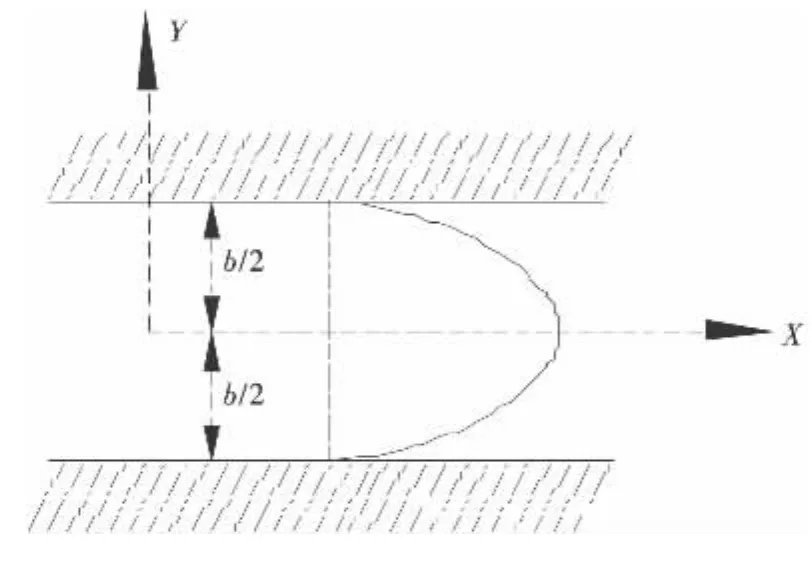
图2 裂隙水流速分布图

1.5 时间、空间离散及求解

对控制微分方程（2），时间离散采用一维差分格式，空间离散采用迎风加权的有限元格式，以避免传统伽辽金有限元格式所遇到的数值震荡问题［15］.方程除了包含热传导，也考虑了裂隙水流的热传输，最终离散所得线性方程组的系数矩阵具有病态、非对称等特点，为保证求解过程的数值稳定性、收敛性，提高计算效率，需采用特殊的数据存储及方程求解技术，传统的一维半带宽存储技术及平方根分解方法不再适用.

2 计算结果分析

2.1 裂隙宽度对温度场的影响

为比较裂隙宽度对岩体温度场分布的影响，本文计算获取了裂隙水最大流速为1.0×10－4m／s，裂隙宽度分别为0.5、1、1.5、2和2.5mm 时的岩体稳定温度场.裂隙中心水温沿裂隙分布曲线如图3所示，结果表明当流入水温低于岩体温度时，裂隙中心水温沿流程递增；在裂隙中心的相同处，水温随裂隙宽度的增加而减小.此外，图3也表明水温沿裂隙变化率取决于裂隙水与岩石的温差，温差越大，变化越显著.

图4～5分别呈现了裂隙宽度为0.5mm和2.5 mm时的最终稳定温度分布情况，结果总体表明，当裂隙水温低于岩石温度时，裂隙岩体稳态温度场分布随裂隙宽度的增大而呈减小的趋势.

图4 b＝0.5mm时裂隙岩体稳定温度分布

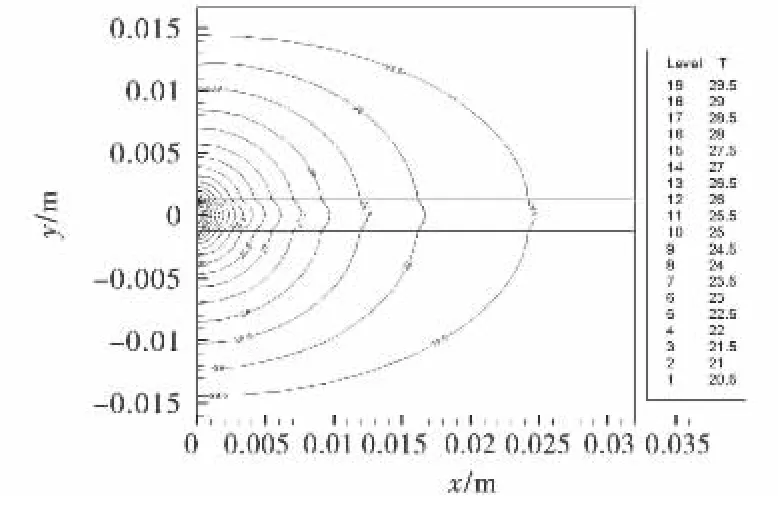
图5 b＝2.5mm时裂隙岩体稳定温度分布

2.2 流速对温度场的影响

本研究计算分析了裂隙宽度b＝1mm，裂隙水流最大速度分别为0.000 1、0.000 5、0.001、0.002和0.005m／s时的温度场.当水温低于岩体温度，不同流速对应的裂隙中心温度沿裂隙分布曲线如图6所示，结果表明裂隙流速对裂隙水温度影响显著；图7分别表示了垂直裂隙向，离裂隙中心由近到远的A、B、C、D、E、F、G（如图8所示）7个点处温度随裂隙水流速变化分布情况，结果表明远离裂隙中心的位置温度基本呈线性变化，裂隙中心附近位置点的温度变化呈现明显的非线性变化，同时可以看出，裂隙水流速对于这7个参考点的温度影响较大，流速越大，岩石的温度梯度越大，温差越显著.

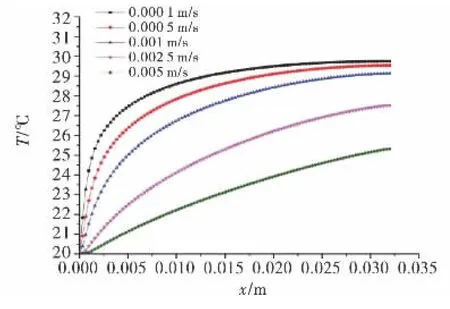
图6 1mm裂隙中心水流温度与流速关系

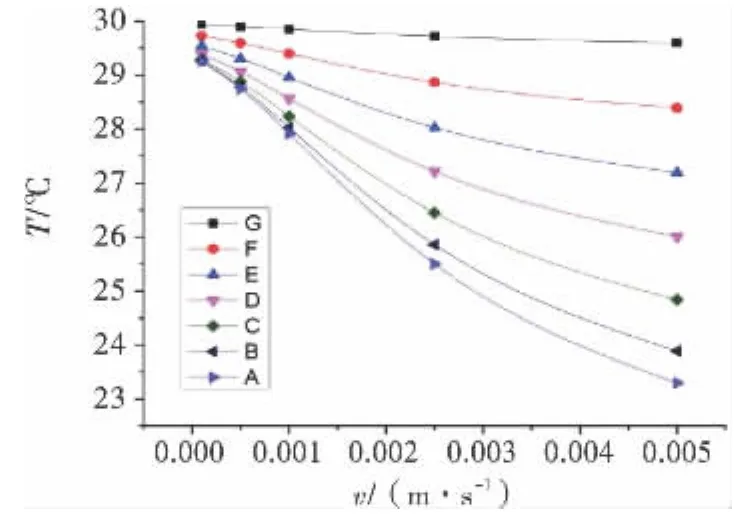
图7 特征点温度随流速变化曲线

图8～9分别呈现了裂隙水流速为5.0×10－4m／s和5.0×10－3m／s时的最终稳定温度分布情况.结果表明，裂隙宽度一定时，裂隙岩体的准稳态温度场随不同量级裂隙水流变化明显.

图8 b＝1.0mm，v＝5.0×10－4 m／s时裂隙岩体温度分布

图9 b＝1.0mm，v＝5.0×10－3 m／s裂隙岩体温度分布

3 结 语

基于水－岩耦合传热控制微分方程，采用有限单元法计算分析水流通过简单裂隙岩体的温度场.主要研究了裂隙宽度、裂隙水流速等关键因素对水－岩耦合传热的影响.在裂隙水流速不变条件下，裂隙宽度变化对水流耦合传热的影响并不显著.裂隙单宽一定时，周边岩体温度场分布对裂隙水流速较为敏感.当裂隙岩体温度高于裂隙水温时，裂隙周边区域的岩石温度随裂隙水流速增大而呈非线性递减趋势.裂隙内渗流流速是决定裂隙岩体温度场的主要因素.

［1］ 张有天.岩石水力学与工程［M］.北京：中国水利水电出版社，2005.

［2］ BRUEL D.Modelling Heat Extraction from Forced Fluid Flow Through Stimulated Fractured Rock Masses E－valuation of the Soultz－Sous－Forets Site Potential［J］.Geothermics，1995，24（3）：439－450.

［3］ Kolditz O.Modelling Flow and Heat Transfer in Fractured Rocks Conceptual Model of A 3－D Deterministic Fracture Network［J］.Geothermics，1995，24（3）：451－470.

［4］ Pestov I.Modelling Structured Geothermal Systems：Application of Dimensional Methods ［J］.Mathl.Comput.Modelling，1997，25（7）：43－63.

［5］ 王如宾，方 涛，徐维生，等.单裂隙水流稳定温度场初探［J］.灾害与防治工程，2005（2）：44－48.

［6］ 王如宾.岩体离散裂隙网络渗流场与温度场耦合分析［D］.宜昌：三峡大学，2007.

［7］ 路 威，项彦勇.单裂隙岩体渗流－传热解析解及参数敏感度分析［A］.和谐地球上的水工岩石力学［C］.第三届全国水工岩石力学学术会议，中国上海，2010.

［8］ 张树光，赵 亮，徐义洪.裂隙岩体传热的流热耦合分析［J］.扬州大学学报：自然科学版，2010（4）：61－64.

［9］ 刘学艳，项彦勇.米尺度裂隙岩体模型水流－传热试验的数值模拟分析［J］.岩土力学，2012（1）：287－294.

［10］白兰兰.裂隙岩体热流模型研究［D］.南京：河海大学，2007.

［11］赵 坚.岩石裂隙中的水流－岩石热传导［J］.岩石力学与工程学报，1999（2）：1－5.

［12］徐义洪.渗流作用下深部矿场采动围岩的传热机理研究［D］.沈阳：辽宁工程技术大学，2009.

［13］董海洲，罗日洪，张 令.岩石单裂隙渗流－传热模型及其参数敏感性分析［J］.河海大学学报：自然科学版，2013（1）：42－47.

［14］张树光，徐义洪.裂隙岩体流热耦合的三维有限元模型［J］.辽宁工程技术大学学报：自然科学版，2011（4）：505－507.

［15］章本照.流体力学数值方法［M］.北京：机械工业出版社，2003.