全寿命费用的DEA优化逐步回归分析法及其应用

秦 珩，张小海

● （1.海军训练舰支队，辽宁大连 116018；2.海军驻上海七○四所军代表室，上海 200031）

全寿命费用的DEA优化逐步回归分析法及其应用

秦 珩1，张小海2

● （1.海军训练舰支队，辽宁大连 116018；2.海军驻上海七○四所军代表室，上海 200031）

在全寿命费用估算建模领域，逐步回归能对多因素进行筛选，克服了建模因素之间的多重相关性对最小二乘估计的干扰。逐步回归分析法本质上是对数据平均趋势的估算，无法避免“由失真数据得到无效模型”的根本问题。为此，提出用数据包络分析(DEA)优化逐步回归的建模方法，用 DEA方法对数据进行评价，剔除无效数据，将有效的数据用来逐步回归建模。该方法能有效克服干扰数据对提取成分的影响，弥补逐步回归方法的不足。通过实例计算并与逐步回归、多元线性回归比较分析，DEA优化逐步回归建模精度为2.64%，高于逐步回归的3.39%和多元线性回归的3.49%，具有实用价值。

全寿命费用；逐步回归分析；数据包络分析；多重相关性模

0 引言

在全寿命费用估算应用领域，多元回归分析是常用的建模方法。用多元回归分析建模时，多重相关性问题常常导致最小二乘估计失效，逐步回归分析法[1]能对建模因素进行筛选，从而降低因素之间多重相关性对回归建模的影响。回归统计建模方法本质上是对平均趋势的估算，无法避免“由失真的数据得到无效的模型”根本问题。在实际回归分析建模时，由于各个时期的数据样本有效程度不等，而回归分析对此并不加以区分。因此，得到的计算结果是“平均值”，不能提供“最优值”，鉴于数据包络分析（DEA,Data Envelopment Analysis）方法可对数据是否有效进行评价“优选”，克服一般回归分析方法的“平滑性”，进行“最优性”回归建模预测[2]。鉴于此，本文提出用DEA优化的逐步回归分析的全寿命费用估算方法。

1 DEA理论

数据包络分析(DEA)是以相对效率概念为基础发展起来的一种效率评价方法，自1978年第一个DEA模型—C2R模型发表后，相关的研究不断涌现，至今已形成关于效率、生产可能集、生产前沿面等概念的完整的理论、方法和模型，并广泛应用于管理科学、系统工程和决策分析等各个领域，DEA已成为管理科学与系统工程领域处理复杂问题的重要而有效的分析工具[3]。文献[4]介绍了DEA的起源，模型等内容；文献[5]将DEA二次相对评价法对装备效费进行评价，明确了非有效决策单元的调整量；文献[6]将DEA、PCA及数值分类方法结合起来用于制造业中的能源消耗使用效率评价，但至今未见DEA在逐步回归建模方面的应用。

DEA的基本模型：假设n决策单元 DMU1、DMU2、…，DMUn，每个DMU有m种输入和s种输出，DMUj的输入和输出向量分别为xj=(x1j，x2j，…xmj)T，yj=(y1j，y2j，…ysj)T，j=1，2，…n。

设DMUj0的输入、输出为(xj0，yj0)，这里简记为(x0，y0)，评价DMUj0相对有效性的C2R模型为：

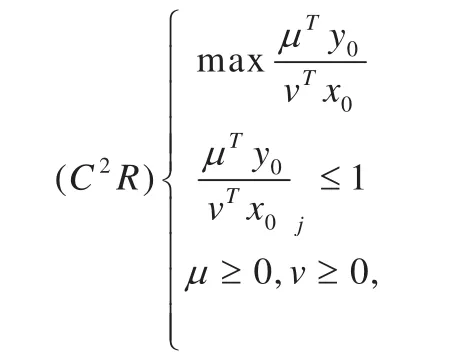
其中：v=(v1，v2，…vm)T，u=(u1，u2，…us)T分别为m种输入和s种输出的权系数。利用Charnes和Cooper关于分式规划的Charnes-Cooper变换：

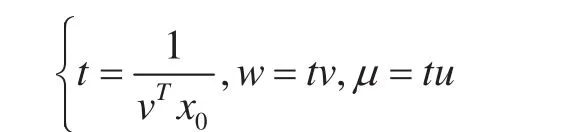
2 用DEA优化逐步回归分析

逐步回归分析法的基本思想是：从所有解释变量中先选择影响最为显著的变量建立模型，然后再将模型之外的变量逐个引入模型；每引入一个变量，就对模型中的所有变量进行一次显著性检验，当原引入的变量由于后面变量的引入而变得不再显著时，将其剔除；逐个引入—剔除—引入，反复这个过程，直到既无显著变量引入回归方程，也无不显著变量从回归方程中剔除为止[1]。

直接采用 DEA中的应用模型可不需要先验信息直接对数据进行评价筛选，因此，在进行逐步回归分析之前，利用DEA评价出有效的数据来进行逐步回归建模。

计算方法和步骤：

1）采用DEA中的C2R模型，将多个自变量作为输入指标，y作为单变量输出指标，利用线性规划的对偶理论求解得θ的效率值，采用有效的数据即效率θ=1的数据来进行逐步回归建模。

2）明确引入变量的“贡献”值，即为变量的偏回归平方和：

3）在判断变量的作用是否显著前，给出引入和剔除变量的F值的下限Fα引和Fα剔回归。

4）计算标准增广矩阵R(0)。

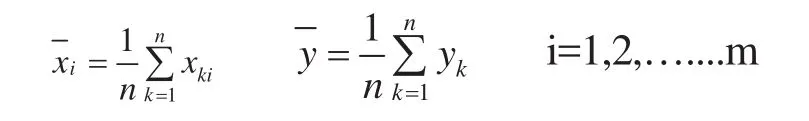
b）计算正规方程组系数：

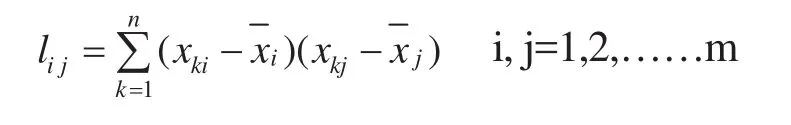
c）构成正规方程组系数矩阵的增广矩阵：

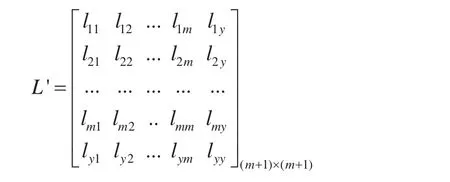
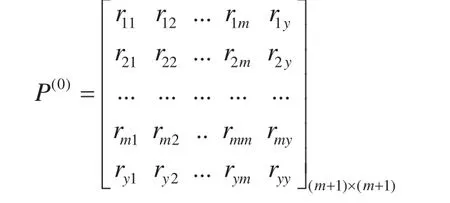
5）引入一个变量计算

c）进行F检验，，若F引>Fα引，则引进该变量，并进入；

d）否则，结束整个逐步回归过程；4)对增广矩阵R(l)进行变换(已经引进了一个变量)，使R(l)→R(l+1)，则：

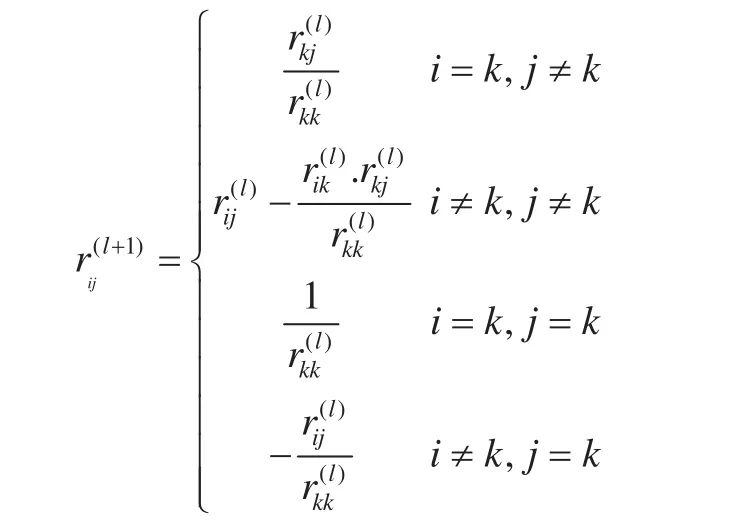
其中，k是被引进或剔除的变量的下标。

6）剔除一个变量计算

b）求出Uil的最小者，

c）进行F检验，若，F剔>Fα剔，则该变量不予剔除，终止剔除过程，否则，剔除该变量，并进入d）；

d）对标准增广矩阵R(l)进行变换，计算方法同4）-d）。

7）循环步骤4）和5），直到没有变量进出，计算终止。

3 实例分析

为体现客观性，现采用文献[7]中刀具磨损实验数据，来验证DEA优化逐步回归建模方法的实际应用价值。刀具磨损数据见表1。

将此5个自变量的10组数据作为DEA应用模型的输入，y作为DEA应用模型的输出代入C2R模型中，利用MATLAB求解，可以算出各组数据的相应最优值θ，计算结果如表2所示。

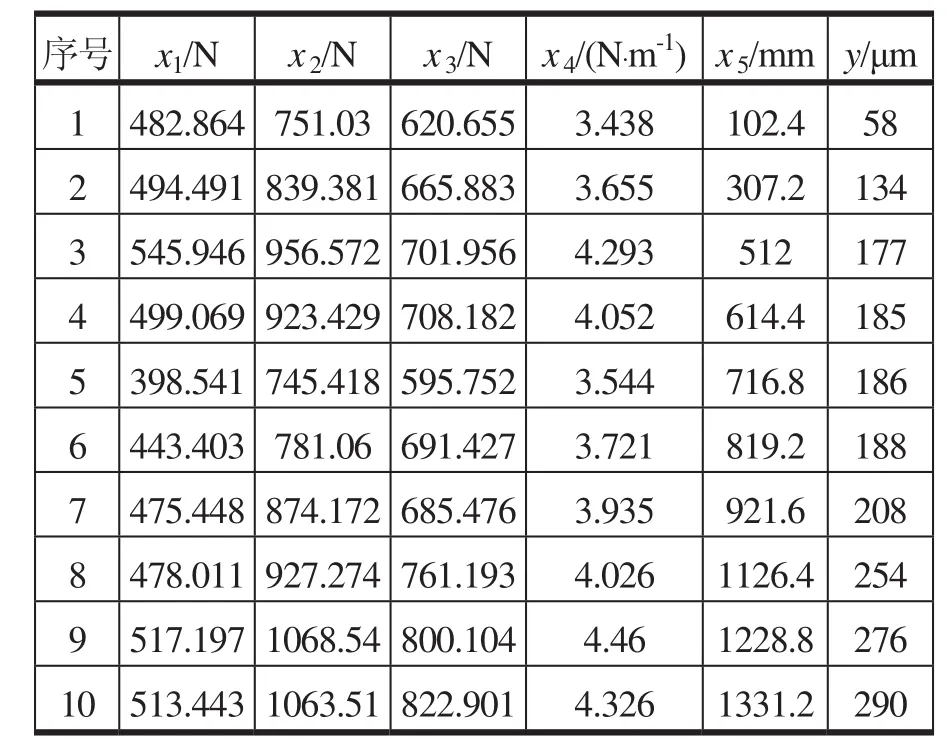
表1 实验数据

表2 DEA评价结果

从表2中剔除效率值θ<1的序号为6，7两组数据，将表2中效率值θ=1的序号1，2，3，4，5，8，9，10组数据作为逐步回归分析的建模数据，数据如表3所示。

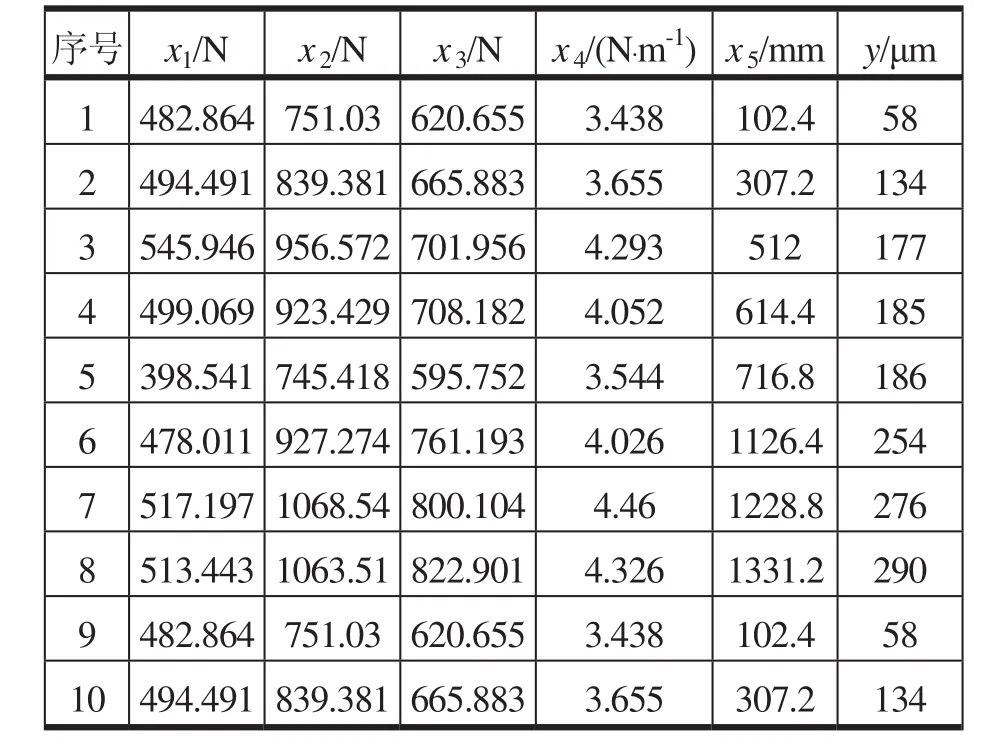
表3 建模数据

将表3的数据进行逐步回归分析。根据文献[7]可知，实验数据的y与自变量之间是成指数关系的，因此，将表3的数据进行以10为底的对数变换得表4。进行逐步回归分析，之后再反变换还原方程，即可得y与x的方程。

对表4的数据进行逐步回归分析得表5，最终确定变量为x1、x3、x4、x5，建立模型为：

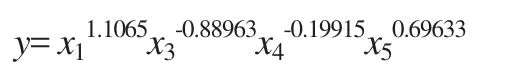
平均绝对误差为：2.64%。

若在DEA评价后，经对数变换后采用多元线性回归建模，其平均绝对误差为：2.65%。

在此，将表1的数据未通过DEA评价，直接进行逐步回归作为比较，以体现DEA优化逐步回归分析建模的优势。

表4 对数后建模数据

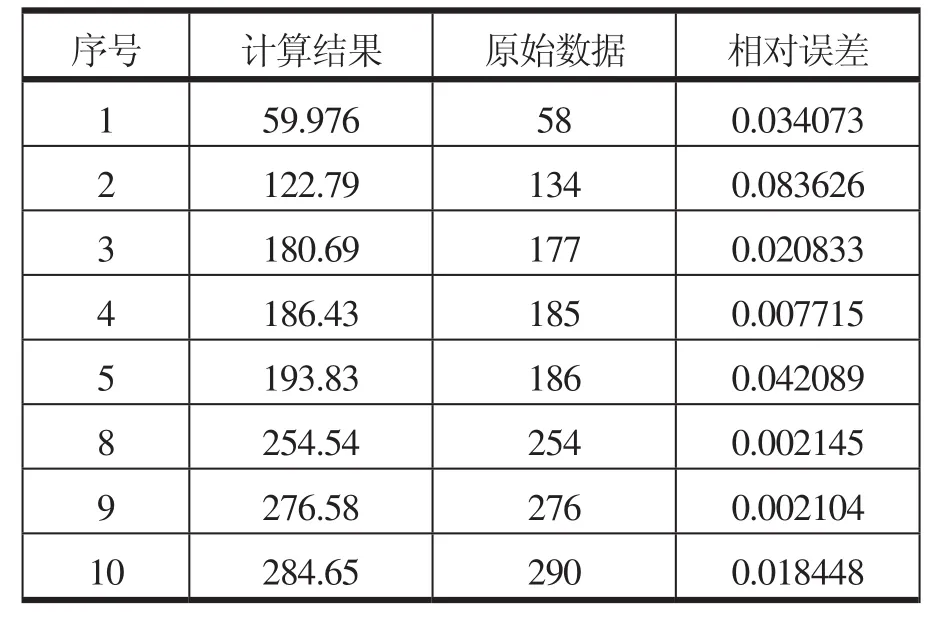
表5 回归计算结果

采用同样的方法对数据进行处理，数据对数变换后进行逐步回归分析计算，通过分析，最终确定变量为x2、x3、x5。

最终得回归方程为：

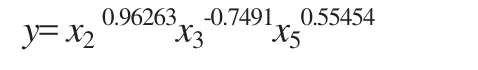
平均绝对误差为：3.39%

同样，将表1的数据取对数变换，多元线性回归分析计算得平均绝对误差为3.49%。

若对表1数据直接进行回归计算，其平均绝对误差为5.60%，说明原始数据服从指数关系是有科学依据的。

4 结论

1）提出用DEA优化逐步回归分析法，建模精度高。通过综合DEA评价数据的有效性，利用有效数据进行逐步回归建模，有效克服了无效数据对回归建模的影响。通过实例分析多元线性回归、逐步回归分析法进行对比，DEA优化逐步回归建模精度为2.64%，多元线性回归建模精度为3.49%，逐步回归分析精度为3.39%，该方法具有一定的实用价值。

2）用DEA优化逐步回归方法突出利用有效的数据建立有效的回归模型的思想，克服了常用的回归统计建模方法无法避免“依据错误数据得到错误的模型”的不足。建立了以费用最优为目标的回归模型，这对于进行全寿命费用的科学预测，具有重要意义。

[1]狄鹏,胡涛,杨建军.预测与决策[M].北京:国防工业出版社,2007.

[2]段永瑞.数据包络分析—理论和应用[M].上海:上海科学普及出版社,2006.

[3]Cooper W W,Seiford L M,Tone K.Data Envelopment Analysis[M].Kluwer Academic Publisher,Boston,Dordrecht,London,2000.

[4]魏权龄.数据包络分析[M].北京:科学出版社,2003.

[5]廖武,陈云翔,孟飙.基于 DEA 的装备费效分析[J].计算机工程与应用,2007,43(9):219-222.

[6]Azadeh A,Amalnick M S ,Ghaderi S F ,et al.An integrated DEA PCA numerical taxonomy approach for energy efficiency assessment and consumption optimization in energy intensive manufacturing sectors[J].Energy Policy,2007,35:3792–3806.

[7]王惠文,吴载斌,孟洁.偏最小二乘回归的线性与非线性方法[M].北京:国防工业出版社,2006.

Optimized Stepwise Regression Analysis with DEA and Its Application

QIN Heng1,ZHANG Xiao-hai2
(1.1.Navy of Training Ships Detachment,Dalian 116018,China; 2.Navy Representative Office at No.704 Research Institute of CSIC,Shanghai 200031,China)

Stepwise regression filters independent variables while modeling,which overcome the multi-correlation between independent variables that disturb the least squares estimation in the life cycle cost modeling.The regression statistical modeling approach estimates the average trend of the data essentially,which cannot avoid the problem that obtain the wrong model according to the error data at all.Therefore,the optimized stepwise regression with Data Envelopment Analysis (DEA) was proposed to overcome the problem,which can evaluate the efficiency of the data and remove the inefficiency data for stepwise regression modeling.The new approach can overcome the effect of the disturbed data when filtering principal components in the independent variables.Compared with the method of stepwise regression and multiple linear regression,the precision of the optimum stepwise regression with DEA is 2.64%，which is higher than stepwise regression with 3.39% and multiple linear regression with 3.49%.

life cycle cost (LCC); stepwise regression analysis; data envelopment analysis (DEA); multi-correlation

N945.11

A

秦珩（1976-），男，工程师。主要研究方向：机电管理。