基于纯方位信息的多传感器航迹融合仿真分析

张中科，方 青，田明辉

（中国电子科技集团公司38所，合肥230088）

0 引 言

随着科技的发展，战场上应用的传感器种类越来越多，除传统的有源传感器雷达外，又涌现出了雷达侦察、通信侦察、光电侦察等无源传感器。雷达能够提供比较准确的目标距离、方位信息，但是存在低空盲区，容易遭受电子干扰和反辐射导弹。相对于雷达来说，无源传感器不易被敌方察觉，探测距离更远，可以提取辐射源的信号参数，完成对辐射源目标的型号识别和属性推理。利用不同类型的传感器进行协同探测，可发挥它们各自的优势，获得单个传感器无法实现的作战效能，提高系统的可靠性和生存性。

多传感器航迹融合通常是利用无源、有源传感器都能获得的目标方位信息，把雷达探测到的目标位置信息同无源传感器得到的该目标的属性信息综合起来，主要包括航迹关联和航迹融合2个过程。其好处在于：一方面，利用所获得的综合信息可以实现对目标特性更深刻、更准确的理解；另一方面，通过方位参数的融合可以获得目标更加准确的方位信息。

有很多学者开展了这方面的研究工作［1－8］，文献［2］、［6］、［7］、［8］利用不同的数学工具建立电子侦察－雷达航迹的融合模型，文献［4］仿真分析了不同算法的航迹融合性能，文献［5］将3类传感器的方位信息按照时间顺序统一后，对目标进行跟踪滤波。但是，现有的基于纯方位信息的传感器航迹融合算法研究存在以下问题：一是，现有算法没有系统讨论传感器测量精度、异类传感器测量精度差异、测量数据率对航迹关联融合性能的影响；二是，现有算法都是基于航迹相似度测度的，适用于2类传感器航迹之间的两两融合，但是对于3类以上传感器航迹关联融合来说，由于不同类型的传感器性能不一样，不同的融合方法和融合顺序对算法性能有着显著的影响，现有工作缺少对该问题的讨论。为此，本文围绕着现有工作存在的不足开展了相关研究。

1 基于纯方位信息的多传感器航迹关联算法

利用目标方位信息对多个传感器航迹进行关联，最终可以归结到2类传感器之间的航迹关联，该问题的严格定义如下：若A、B传感器位于同一个平台之上，设θj（ti）是A类传感器测得的第j个目标的方位值，θe（ti）是B类传感器测得的某目标的方位值。为了判断B类传感器观测到的一条目标航迹TB是否同A类传感器观测到的某条目标航迹TkA关联，首先需要利用判别函数分别计算TB同A类传感器航迹集合 ｛TiA｜i＝1，2，…，n｝中每条航迹之间的相似度，并从中选择最大相似度值Smax，随后分析Smax和门限值之间的关系，依据相关准则判定TB是否关联到 ｛TiA｜i＝1，2，…，n｝中的一条航迹TkA，以及它们之间的关联程度。

从现有文献来看，实用的利用方位信息对多传感器航迹做关联的算法主要有基于统计分析的关联算法和基于模糊分析的关联算法两大类。它们都由3个关键的部分构成，分别是判别函数、判别门限、判别准则。其中，判别函数都包含表达式：

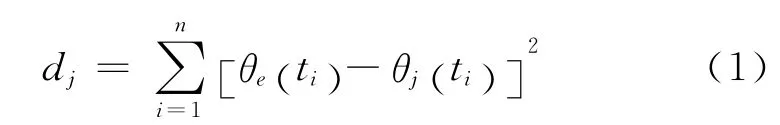
dj越大，航迹相似度越低；门限值的设定基于判别函数并建立在概率分析模型基础之上；判别准则主要是根据航迹相似度和门限值之间的关系给出航迹关联程度定义，例如确认关联、暂时关联、确认无关、暂时无关等。两类算法之间差异主要表现在这三部分设定方法上的不同，具体描述可参考文献［3］、［4］，限于篇幅本文不再详细描述。

2 算法性能分析

2.1 关联概率分析

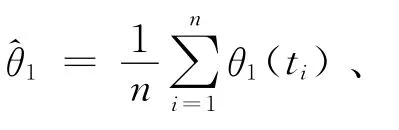
不难发现，如果d2＞d1，则2类传感器的航迹正确关联；若d2＜d1，则航迹关联错误。为了讨论d1、d2之间的大小关系，首先计算下式：

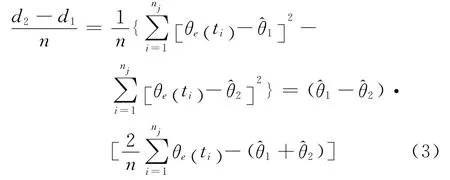
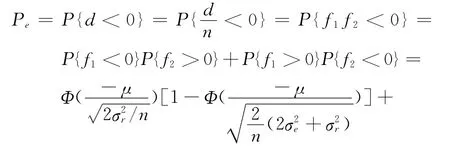
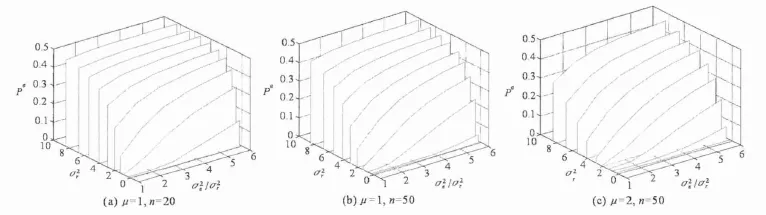
图1 错误关联概率和σ2e／σ2r、σ2r、μ、n之间的关系

（2）错误关联概率Pe和存在同趋势增长关系，越大，Pe越大，但是对Pe的影响程度没有大。

（3）错误关联概率Pe还受到μ和n的影响。目标真方位间隔μ越小，说明目标在方位上越临近，因此将会导致错误关联概率升高。观测样本容量n对于Pe也有着较大影响，n越大，说明航迹关联的数值依据越充分，因此判断错误的可能性也就随之降低，所以错误关联的概率Pe会越小；反之，如果观测样本容量不足，Pe也会随之上升。

2.2 融合精度分析

假设目标的真实方位角为θ，2类不同侦察设备方位角测量误差均值为0，方差分别为的任意分布（高斯、均匀），则有：

将2个侦察设备的方位角测量值进行线性加权融合，得到融合后的方位估计值为：

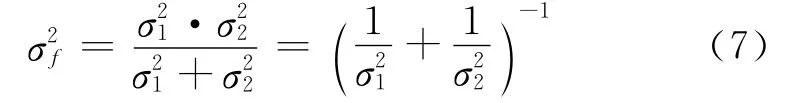
若将2类不同侦察设备的方位值线性加权融合表示为二元运算符“·”，将侦察设备1方位测量值θ1和侦察设备2方位测量值θ2线性加权融合处理表示为代数式θ1·θ2，它满足下面2条规律：

（1）运算符“·”满足交换律，即θ1·θ2＝θ2·θ1；

（2）运算符“·”满足结合律，（θ1·θ2）·θ3＝θ1·（θ2·θ3）；

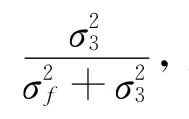
3 多传感器航迹融合方法

通过上一节的分析可以发现：首先，多传感器航迹融合应优先选择将低精度传感器测得的目标航迹向高精度传感器测得的目标航迹关联，才能比较准确地将航迹关联起来；其次，对于航迹方位线性加权融合来说，多传感器航迹融合的顺序不会影响到最终的融合方位结果；再次，航迹融合除了可以将不同传感器的侦察信息综合起来之外，还可以获得更精确的目标方位信息。

在实际环境中，目标的距离和运动特性会导致在一定时间内不是所有传感器都能侦测到目标。对于航迹融合来说，通常必须要有2类或2类以上航迹才能进行航迹融合。现假定有源传感器雷达航迹的方位精度优于无源侦察传感器的方位精度，因此，航迹融合按照以下原则进行融合：

（1）在2类传感器有侦察结果的情况下，对这2类航迹进行航迹关联。

（2）在3类以上传感器都有侦察结果的情况下，将低精度航迹（如通信侦察航迹、雷达侦察航迹）分别同高精度航迹（如雷达航迹）关联。

4 仿真实验结果分析

场景配置：以观测站为中心，在120°范围内生成若干条目标航迹，目标速度在180～340m／s范围之内随机选取，目标的径向距离在50～600km范围变化。有源传感器数据率为10s／次，无源侦察数据率为1s／次。仿真中的目标方位测量值通过在目标真实方位上添加白噪声生成，其中，雷达测量噪声为［－1°，1°］之间均匀分布的数值，无源侦察测量噪声为［－2°，2°］之间均匀分布的数值。蒙特卡洛实验次数为100次，每次实验场景运行300s，实验设定的允许误相关概率门限α和漏相关概率门限β分别为0.05。图2显示目标个数不同的场景中的目标分布和运动情况，图2中的“＊”为航迹起点。

实验方法：航迹关联算法通常只能判定2个航迹之间的关联关系，由于有源雷达、雷达侦察设备、通信侦察设备工作是彼此独立的，因此，如果3个设备处理的航迹同时更新，则分别独立地进行雷侦航迹和雷达航迹关联、通侦航迹和雷达航迹关联，否则，对更新的2个航迹进行关联。

实验结果分析：

2类航迹关联方法：对于一类航迹中的任意一条航迹，从另一类航迹中找到关联度最大的一条航迹，根据高、中、低门限值来判断2条航迹的关联程度，即为前面所述4类：确认关联、暂行关联、暂行无关、确认无关。

实验结果主要从正确关联率、错误关联率、漏关联率3个方面来衡量：

对于源于同一个目标的2类航迹，若关联程度被判定为确认关联或者连续被判定为暂行关联，认为这是一次正确的关联。

对于源于同一个目标的2类航迹，若关联程度被判定为确认无关或者连续被判定为暂行无关，认为这是一次漏关联。对于源于不同目标的2类航迹，若关联程度被判定为确认关联或者连续被判定为暂行关联，认为这是一次错误的关联。

图2 不同目标个数的场景

如图3所示，关联性能受到关联步长的影响，所谓关联步长是指被用于关联的数据的时间跨度。在同一个场景下，关联算法采用的关联步长越长，关联的正确率越高，误关率和漏关率越低。但是关联步长变长，会造成融合航迹更新速率降低。

图3 场景目标个数为20个，不同关联步长的航迹关联结果

如图4所示，区域内目标密集程度对基于方位的航迹关联算法性能存在较大的影响，随着目标个数的增多，正确关联率下降显著，同时误关率较快上升。

图4 场景目标个数不同，关联步长为50s的航迹关联结果

图4和图5场景的主要差异是，图4中一条航迹（雷达航迹）的方位测量误差方差为0.33，另一条航迹（无源侦察航迹）方位测量误差方差为1.33；图5中2条航迹（均为无源侦察航迹）的方位测量误差方差均为1.33。通过对比图4、图5可以发现，测量数据噪声等级影响着关联算法性能，尤其是对于区域内目标比较密集的情况。由于测量噪声变大，当区域内目标密度中等时，正确关联率下降5%左右，误关率上升5%左右；当区域内目标密度较大时，正确关联率下降15%左右，误关率上升18%左右。

通过对比图5、图6可以发现，观测设备的数据率差异同样影响着关联算法性能。图5中2类观测设备的数据率之比为1∶10，图6中2类设备的数据率之比为1∶1，后者相对于前者正确关联率提高了8%左右，错误关联率下降了5%左右。综合比较图4、图5、图6，可以发现，观测设备数据率差异对关联算法性能影响要小于噪声等级对算法性能的影响，这也是在实验方法选择中，采用无源传感器航迹优先和有源传感器航迹关联融合的原因。

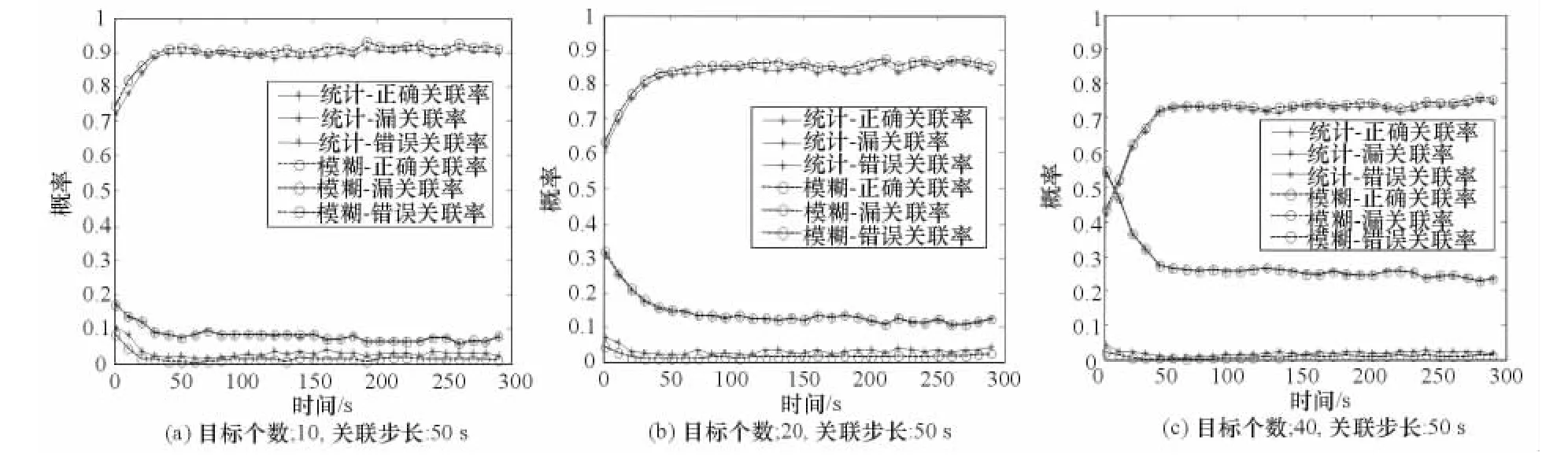
图5 通信侦察和雷达侦察航迹关联（数据率比值：10∶1）

图6 通信侦察和雷达侦察航迹关联（数据率比值：1∶1）

通过实验可以发现，从正确关联率、误关率、漏关率3个方面来看，模糊航迹关联算法的性能均优于统计关联算法。采用50s的关联步长，区域内目标个数适中（120°范围内目标不多于40个），模糊航迹关联算法的正确关联率可以保持在90%左右，错误关联率保持8%左右，漏关率在5%以下，因此实际工程使用中，更倾向于使用模糊航迹关联算法。

图7显示了不同侦察设备的原始方位误差和融合后的方位误差，从图中可以发现实际结果和2.2小节的理论分析结果基本一致。

图7 不同侦察设备方位误差和融合后的方位误差图

也就是说，融合后的方位误差方差小于所有的原始值，特别是当不同侦察设备方位误差方差相近时，最好可以达到原始方差的1／3。但是当不同侦察设备方位误差方差相差较大时，融合的方差和原始误差方差中的最小值相近，也就是说此时融合并没有有效改善方位精度。虽然如此，但是融合仍然有十分重要的意义，因为它能够将不同侦察设备的功能有效地综合起来了，可以为战场决策提供更加全面、丰富的情报信息。

5 结束语

本文首先从理论上分析了传感器测量精度、异类传感器测量精度差异、测量数据率对基于纯方位信息的多传感器航迹融合性能的影响，并根据这些影响因素生成多个不同的场景，开展了仿真实验。实验结果表明，传感器测量精度越高，异类传感器测量精度差异越小，数据关联样本越大，异类传感器航迹关联正确率越高，和理论分析相一致。根据该理论和实验分析结果，本文进一步提出了3类以上传感器航迹融合的方法和原则。在接下来的工作中，将会进一步研究基于多维信息的异类传感器航迹融合的理论和方法。

［1］Wang G H，He Y.Sequential track monitoring with multiple 2－D passive sensors［J］.Journal of Systems Engineering and Electronics Techniques，1998，9（2）：31－39.

［2］Kalandros M，Pao L Y.Multisensor covariance control strategies for reducing bias effects in interacting target scenarios［J］.IEEE Transactions on Aerospace and E－lectronic Systems，2005，41（1）：153－173.

［3］何友，王国宏，陆大唫，等.多传感器信息融合及应用［M］.北京：电子工业出版社，2000.

［4］田明辉，方青，任清安.机载ESM与雷达航迹融合仿真系统研究［J］.雷达科学与技术，2012，10（1）：64－70.

［5］吴巍，王国宏，柳毅，等.机载雷达、红外、电子支援措施协同跟踪与管理［J］.系统工程与电子技术，2011，33（7）：1517－1522.

［6］王妍妍.基于GAM模型雷达与ESM数据关联实现方法［J］.指挥信息系统与技术，2012，3（3）：40－44.

［7］卜卿.D－S证据理论在ESM－雷达航迹关联中的应用［J］.指挥信息系统与技术，2011，2（4）：60－63.

［8］董红波，王刚，刘进忙.机载雷达与ESM航迹关联技术研究［J］.传感器与微系统，2010，29（1）：12－14.