大电网可靠性评估的灵敏度分析新方法
谭文刚,刘 为,靳东一,徐鹏程
(国网四平供电公司调控中心,吉林四平136000)
电力系统可靠性不仅取决于其网络拓扑结构,而且与各系统中元件的参数密切相关,传统可靠性分析方法只能反映出整个系统或负荷点供电的好坏,难于找到钳制系统可靠性的元件信息,而基于拓扑结构的电力系统可靠性灵敏度分析可通过网架结构及元件信息,解决此类问题[1-2]。
文献[3]通过分析各可靠性指标对应的测试函数,利用偏微分的概念推导了失负荷概率LOLP、失负荷频率LOLF、电力不足期望ENDS等指标对元件无效度的灵敏度解析表达式。在此基础上,文献[4]完整地推导了失负荷概率LOLP、失负荷频率LOLF、电力不足期望ENDS等大电力系统可靠性指标对元件有效度、无效度、故障率和修复率的灵敏度。其后,文献[5]采用机组的多状态可靠性模型,考虑了机组的检修计划和运行约束,分别对基荷机组和循环机组进行了可靠性灵敏度分析。但上述这些方法通常仅适用于简单的情况,在需要考虑系统复杂运行工况或元件多状态可靠性模型时,往往难以应对[6-8]。基于此,本文提出了大电网可靠性评估灵敏度分析新方法,即通过元件可靠性信息以及连通关系,求得灵敏度的相关信息,并对系统薄弱环节提出相应指导意见,以解决计算时的复杂程度问题。
1 回路
在过去的输变电设施可靠性基础数据的管理中,可靠性基础数据的统计管理是基于单个元件进行的。在2010年可靠性管理专业会议上,国家电网公司发布了新的《输电系统可靠性评价实施细则(试行稿)》。该实施细则中首次提出了回路的概念,即将连接在传输终端、变电站、或者是系统输电节点之间,具有一定功能的设备组,定义为一个回路。在发输电系统中,主要包括母线回路、变电回路和输电回路3类基本回路。因此,发输电系统可靠性管理将由原来基于单个元件的管理,升级到以回路为基本单元的管理。
2 回路停运模型
2.1 对于母线回路l
导致母线回路失效的原因有一阶故障(某一个元件随机故障或计划检修),也有二阶故障(两个元件随机故障重叠停运、一个元件计划检修期间另一元件随机故障重叠停运)。令一阶故障的元件序号集合为k∈F1,二阶故障的元件序号集合为(i,j)∈F2,则母线回路强迫停运(计划停运期间发生重叠随机停运也归为强迫停运)和计划停运引起的停运概率(年平均停运时间,单位年)分别为
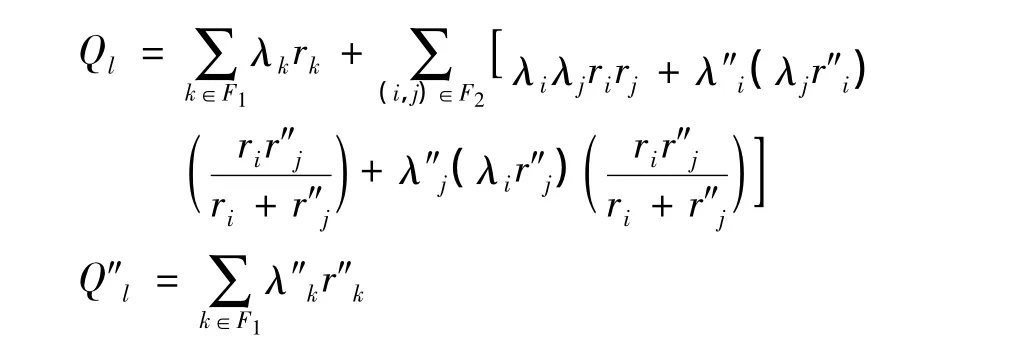
式中:Ql为母线回路强迫停运概率;Q″l为计划停运概率;λi为元件 i的故障率;λ″i为计划停运率;ri为平均故障修复时间;r″i为平均计划停运时间。
对应于强迫停运和计划停运的综合停运概率为上述两式之和。
在此,只考虑到二阶割集,则等效强迫停运率和计划停运率为

对应于强迫停运和计划停运的等效平均修复时间分别为

此时,回路l的各个参数对元件i的各个参数的灵敏度则可按元件一阶故障事件以及二阶重叠故障事件进行求解。
2.2 对于线路或变压器回路l
对于线路或变压器回路l,从可靠性等值网络的角度,可以将其看成由所属元件组成的串联系统,故回路参数可按相加考虑,此处不予以赘述。
3 基于最小割集法的母线节点供电可靠性及灵敏度分析
假设因电网中其它回路的随机故障、计划停运期间重叠随机故障或该母线本身计划检修或随机故障,导致该母线回路l失效,令最小割集故障事件共有 n 个,即 C1、C2、…、Cn,则母线回路 l的不可靠度和失效频率分别为

该表达式的上限估计为

其上限估计相对容易,只需计算P(Ci),但下限估计涉及到P(Ci∩Cj)的计算,尤其当多重计划检修和多重随机停运重叠发生时,P(Ci∩Cj)的计算比较复杂,因此下面仅以上限估计进行分析,且假定割集事件最高到三阶。
对于母线节点不可靠度对元件可靠性参数的灵敏度分析,将分为两步计算:母线节点不可靠度对回路可靠性参数的灵敏度,以及在此基础上求解其对元件可靠性参数的灵敏度。母线节点不可靠度对回路可靠性参数的灵敏度相当于P(Ci)与f(Ci)对回路可靠性参数的偏导数之和。因此,计算该方面灵敏度时,其关键在于计算P(Ci)和f(Ci)对回路可靠性参数的偏导数。假设考虑最高到三阶割集,约有10种情况应对其进行赋值计算。
基于上述计算结果,最终可得母线节点不可靠度对回路l中元件i的可靠性参数,即强迫停运率λi、计划停运率 λ″i、平均故障修复时间 ri、平均计划停运时间r″i的灵敏度。
1)强迫停运率λi的灵敏度:

2)计划停运率λ″i的灵敏度:
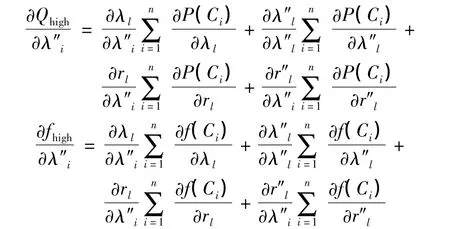
3)平均故障修复时间ri的灵敏度:

4)平均计划停运时间r″i的灵敏度:
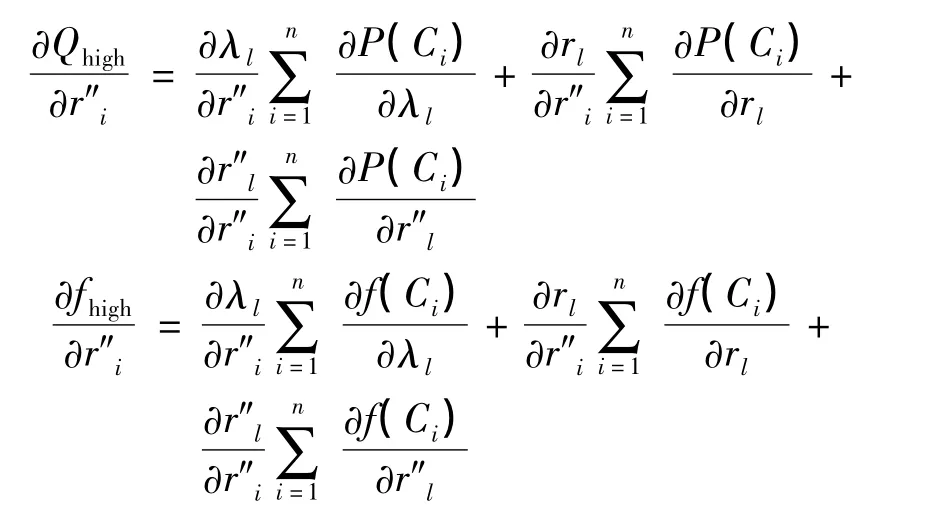
4 算例验证
采用FORTRAN软件编写了基于拓扑结构的大电力系统可靠性灵敏度分析程序,对CEPRI-36系统节点算例进行了计算分析,列出了CEPRI-36系统的计算和分析结果,其中,2个节点(BUS13为电源点)的可靠性指标,如表1所示,其可靠性评估灵敏度分析(按强迫停运率)结果,如表2、表3所示。

表1 BUS13及BUS27的可靠性指标Tab.1 Reliability indices of BUS13 and BUS27

表2 BUS13的灵敏度分析结果Tab.2 Sensitivity indices of BUS13

表3 BUS27的灵敏度分析结果Tab.3 Sensitivity indices of BUS27
将表2、表3中元件强迫停运率均降低1次/a,再计算的各点可靠性指标如表4、表5所示。

表4 元件可靠性参数改变后BUS13的可靠性指标Tab.4 Reliability indices of BUS13 after component reliability parameters are changed
从表4、表5中可以看出:对于某点灵敏度较高的元件,将元件相应参数改变相同数量级,灵敏度较高元件所提升的可靠性越高。

表5 元件可靠性参数改变后BUS27的可靠性指标Tab.5 Reliability indices of BUS27 after component reliability parameters are changed
5 结语
基于拓扑结构的大电网灵敏度分析程序,并根据电网网架连接关系,可快速分析出对某一节点可靠性影响较大的节点。而且,这些灵敏度指标在基于拓扑结构可靠性分析应用中,能助于有效找到某节点的可靠性薄弱点,提供改善节点可靠性的措施,为全网可靠性的提升提供借鉴指导。
[1]BILLINTON R,ALLAN R N.Reliability evaluation of power systems(Second Edition)[M].New York and London:Plenum Press,1996.
[2]国家电力监督委员会电力可靠性管理中心.电力可靠性技术与管理培训教材[M].北京:中国电力出版社,2007.National Electric Power Supervision Committee Reliability Management Center.Training materials of electric power reliability technology and management[M].China Electric Power Press,2007.
[3]A.C.G.Melo,M.V.F.PEREIRA.Sensitivity analysis of reliability indices with respect to equipment failure and repair rates[J].IEEE Transactions on Power Systems,1995,10(2):1014 1021.
[4]赵渊,周念成,谢开贵,等.大电力系统可靠性评估的灵敏度分析[J].电网技术,2005,29(24):25 30.ZHAO Yuan,ZHOU Niancheng,XIE Kaigui,et al.Ssensitivity analysis method for reliability evaluation of bulk power system[J].Power System Technology,2005,29(24):25 30.
[5]H.SALEHFAR,S.TRIHADI.Application of perturbation analysis to sensitivity computations of generating units and system reliability[J].IEEE Transactions on Power Systems,1998,13(1):152 158.
[6]YUAN ZHAO,NIANCHENG ZHOU,JIAQI ZHOU,et al.Research on Sensitivity Analysis for Composite Generation and Transmission System Reliability Evaluation[C].International Conference on Power System Technology,2006:1 5.
[7]赵渊,周家启,周念成,等.大电力系统可靠性评估的解析计算模型[J].中国电机工程学报,2006,26(5):19 25.ZHAO Yuan,ZHOU Jiaqi,ZHOU Niancheng.An analytical approach for bulk power system reliability assessment[J].Proceedings of the CSEE,2006,26(5):19 25.
[8]M.MASOOD AHMAD,ATIF DEBS,YORAI WARDI.Estimation of the derivatives of generation system reliability indices in monte carlo simulation[J].IEEE Transactions on Power Systems,1993,8(4):1448 1454.

