一种基于主动视觉的非线性摄像机自标定

禹旺勋 YU Wang-xun；王爱菊 WANG Ai-ju

（①昆明理工大学津桥学院工学系，昆明 650106；②云南师范大学商学院会计学院，昆明 650106）

（①Department of Engineering，Oxbridge College，Kunming University of Science and Technology，Kunming 650106，China；②Department of Accounting，Yunnan Normal University Bussiness School，Kunming 650106，China）

0 引言

摄像机标定是从二维图像获取三维信息的必不可少的步骤。空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系由几何模型决定，通过试验和计算获得摄像机内参数和外参数的过程称为摄像机标定。传统的标定方法是通过结构的物体（如标定块，标定板等）在图像中的投影计算摄像机的内参数。但是这种方法必须要有标定物，在很多实际应用中难以实现。近年来，摄像机自标定技术以其应用的灵活性得到了很多研究者的重视，但自标定方法最大的不足是鲁棒性差。这主要是由于自标定方法不论何种形式出现，均是基于绝对二次曲线（absolute conic）和绝对二次曲面（absolute quadric）的方法，需要求解复杂的多元非线性方程来计算摄像机的内参数，从而导致运算速度和结果的精度都不理想。而基于主动视觉的摄像机自标定可以克服这个缺点，它是通过控制摄像机做某些特定的运动来获取图像从而标定摄像机的内参数。一般来说，摄像机的模型参数可以线性的求解，因而算法的鲁棒性较高。但是线性模型一般不能准确的描述真实摄像机的几何成像关系，因此对基于主动视觉的非线性摄像机自标定的研究具有十分重要的意义。因此，本文提出一种基于主动视觉的非线性摄像机自标定方法。

1 基础知识

1.1 线性摄像机模型 摄像机的线性模型为针孔模型。空间点的物理坐标和图像坐标之间关系如下：

设空间中某一点P在世界坐标系与摄像机坐标系下的坐标分别是（Xw,Yw,Zw）T与（Xc,Yc,Zc）T，存在如下关系：

空间任一点P在图像上的投影位置p，由透视投影得到如下关系式：

用齐次坐标与矩阵表示上述透视投影关系：

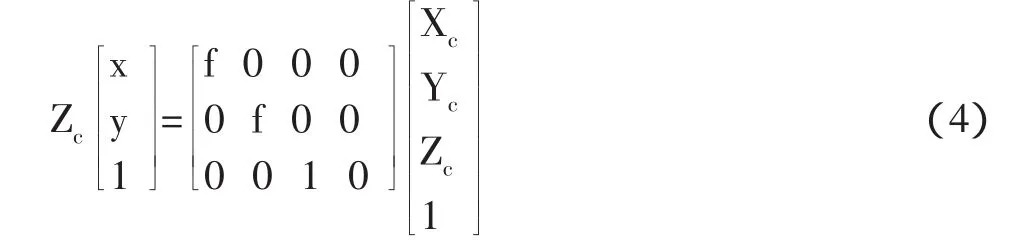
将式（1）与（2）代入（4）式，得到以世界坐标系表示的P点坐标与其投影点p的坐标(u,v)的关系：

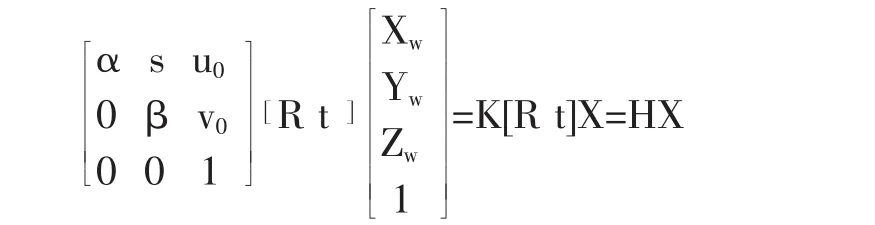
其中，（u0,v0）为主点坐标；α=f/dx为图像轴的尺度因子；β=f/dy为图像轴的尺度因子；s=s′f为畸变因子；H 为3×4矩阵，称为投影矩阵；矩阵K称为内部参数矩阵；[R t]摄像机的外部参数矩阵。

1.2 非线性摄像机模型 摄像机的非线性模型，是指成像过程不服从小孔模型。摄像机的非线性模型可使用下述公式来描述：

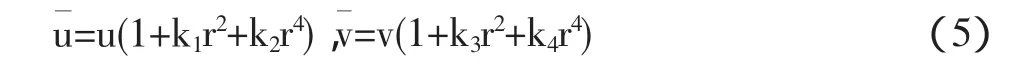
其中r2=u2+v2，式中的k1,k2,k3,k4称为非线性畸变参数。线性模型参数的线性内参数α,β,u0,v0,s与非线性模型的非线性内参数k1,k2,k3,k4一起构成了摄像机的所有内参数。

1.3 主点坐标的确定 纯轴向运动是指摄像机沿光轴方向做平移运动，纯轴向运动特有的性质使其能够应用于摄像机自标定中。根据Ma[4]提出的定理知道，当摄像机作纯轴向运动时，因为光轴方向就是摄像机运动方向，所以对应点连线交点就是运动方向与图像平面的交点，所以对应点连线的交点就是摄像机主点。

水平平移运动是指摄像机在作平移运动时，平移向量为（Xc,0,Zc）；垂直平移运动是指摄像机作平移运动时，平移向量为（0,Yc,Zc）。

设 空 间内任意两点 X1=(Xwl，Ywl，Zwl，1)T，X2=(Xw2，Yw2，Zw2，1)T，对应点连线交于同一点e。X1在摄像机作水平平移前后通过投影矩阵H1，H2投影到图像平面上，投影点为m11=H1X1，m12=H2X1同样可以得到 X2通过投影矩阵 H1，H2投影到图像平面上的投影点m21,m22。mij表示第i个空间点在第j幅图像上的投影点。则m11,m12确定了第一幅图像上关于X1的对应点连线，该直线可以表示为m11×m12。同样，m21,m22确定了第一幅图像上关于X2的对应点连线，该直线可以表示为m21×m22。则对应点连线的交点为e=(m11×m12)×(m21×m22)=(a,b,1)，化简后b的值恰好等于v0。即通过一次水平平移运动可以确定主点的v0值。同理可证在摄像机的畸变因子为零时，通过一次垂直平移运动可以确定主点u0的值。

2 非线性内参数自标定

2.1 非线性内参数约束 在线性模型下，控制摄像机作n组两正交运动，每组正交运动的FOE点，表示为eij(i=1,…,n;j=1,2)，其中i表示第几组正交运动，j表示该组正交运动的第几次运动。如果摄像机作纯平移运动，则为摄像机光心到对应点连线的交点方向。利用每次运动前后由图像对应点连线的交点可以计算出相应的eij。

设已求出eij在图像平面上的坐标为（），则由式（1）和式（3），可以得到eij在摄像机坐标系下的坐标为

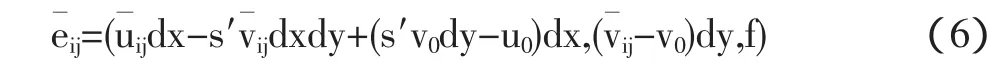
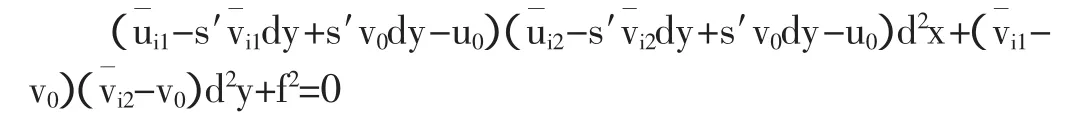
令 h=s′dy，上式两边同除以 f2得

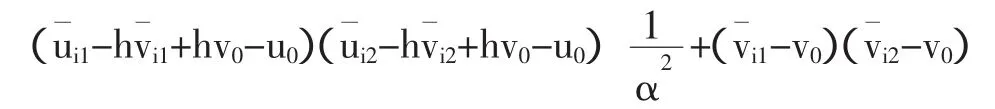
于是，求解非线性内参数问题等价于求解下述优化问题

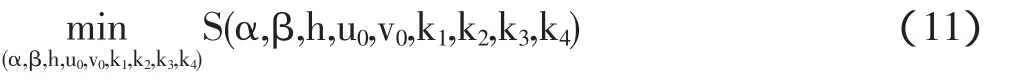
2.2 求解非线性内参数算法 在本文中，将使用变度量法中的DFP技术来求解非线性最小问题[5]。为了叙述方便，将式（11）的变量改写为 X=(x1,x2,x3,x4,x5,x6,x7,x8,x9)。

其中，(x1,x2,x3,x4,x5,x6,x7,x8,x9)=(α,β,h,u0,v0,k1,k2,k3,k4)为非线性的内参数向量；则式（11）应写为

利用DFP算法对式（12）进行求解，从而得出非线性内参数的解。

3 实验

图1为用于非线性摄像机自标定的其中的两组正交运动下的图像，其中十字点被取为图像间的对应点。利用OpenCV中的角点检测函数，检测出一组正交运动下的两幅图像的点对应图像坐标，从而计算出FOE点，然后根据文中所述的基于主动视觉的自标定方法，计算出的非线性的摄像机所有内参数如表1所示。

表1

图1 正交运动下的两组图像

4 结论

由于线性模型摄像机不能准确地描述真是摄像机的几何成像关系，因此对非线性模型的摄像机自标定的研究有很重要的意义。文中探讨了一种基于主动视觉的非线性摄像机自标定方法，通过真实实验数据表明文中提出自标定方法是可行的，精度较高，有一定的实用价值。

[1]邱茂林,马颂德,李毅.计算机视觉中摄像机定标综述[J].自动化学报，2000,26(1)：47-48.

[2]W.Faig.Calibration of close-range photogrammetry systems:Mathematical formulation.Photogrametric Eng.Remote Sensing,41(12):1479-1486,1975.

[3]马颂德,张正友.计算机视觉-计算理论与算法基础[M].北京科学出版社,1998.

[4]Ma S D.A self-calibration technique for active vision system[J].IEEE Trans on Robotics and Automation,1996,12(1):114-120.

[5]吴福朝.计算机视觉中的数学方法[M].北京:科学出版社,2008.

[6]Tsai R Y.An efficient and accurate camera calibration technique for 3D machine vision.In:proc.CV PR’96.364-374.

[7]Hu Zhan-Yi,Wu Fu-Chao.A review on some active vision based camera calibration techniques[J].Chinese Journal of Computer,2002,25(11)：1149-1156.

[8]吴福朝,李华,胡占义.基于主动视觉的摄像机自标定方法的研究[J].自动化学报，2001,27（6）：736-746.

[9]禹旺勋,王爱菊,刘云涛.基于主动视觉的摄像机线性自标定方法.价值工程，2013，32（8）：258-259.