植入式集成磁耦合谐振无线电能传输分析

程瑜华，舒亚明

(杭州电子科技大学射频电路与系统教育部重点实验室，浙江杭州310018)

0 引言

采用4线圈结构的磁耦合谐振无线电能传输方式可以提高效率［1］，实现了中等距离的高效能量传输，但其并未对在植入式医疗应用中情况进行分析。耦合模理论［2］对磁耦合谐振的理论模型进行了详细的理论分析，但是此理论缺乏对实际电路设计的指导。而文献［3］虽然从电路分析角度建立了理论模型，但并不完整;忽略了如第2和第4线圈之间的耦合系数。本文针对植入式集成线圈实现的应用，对磁耦合谐振无线电能传输建立完整和简化的电路理论，分析传输效率，并与传统2线圈电感耦合方式传输效率进行比较。

1 电路理论建模和分析

1.1 完整电路模型

4线圈的无线电能传输等效电路如图1所示。其中，Ln为线圈n的电感值，Cn为线圈n外加串联谐振电容，Rn为线圈 n 的寄生电阻，线圈 m 和线圈 n 之间的耦合系数为 kmn，n=1，2，3，4，m=1，2，3，4。RL为整流电路的输入阻抗。

图1 磁耦合谐振无线电能传输电路模型

当输入电压源工作频率与4个线圈的谐振频率相同时，能量以类似于量子效应中隧道方式进行传输［1］，具有较高的传输效率。本文采用的电压源工作频率与线圈的谐振频率相同。为了有助于理论分析，根据图1中的电压电流关系可以建立电压电流矩阵。

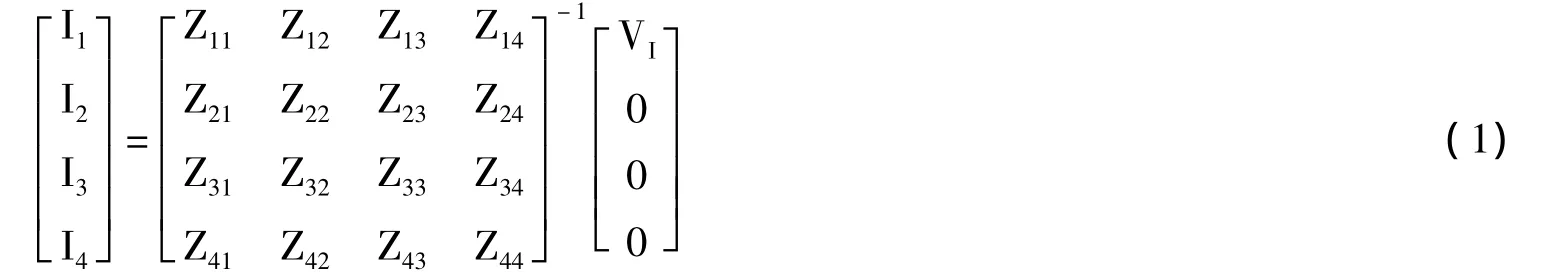
式中，VI为输入电压幅值，In为线圈n上的电流幅值，阻抗Zmn在m=n时为寄生电阻Rn，在m≠n时为线圈m和n之间的互感Mmn，并且满足Mmn=kmn(LmLn)1/2。由式(1)可解得传输效率的表达式为:

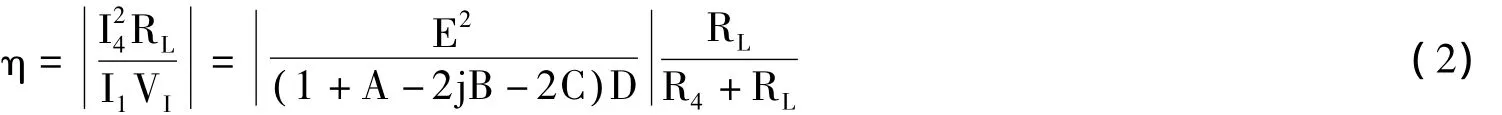
式中，A、B、C、D、E 参数的表达式如下:

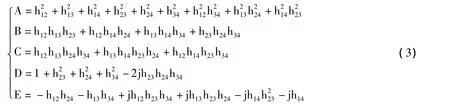
式(3)中，hmn=kmn(QmQn)1/2。从效率表达式可见，耦合系数kmn和线圈Q值Qm、Qn可以作为一个整体考虑。这也体现了磁耦合谐振方式可以在中距离达到较大传输效率的本质原因是通过耦合系数和Q值的互相弥补，使系统达到较大的传输效率。

1.2 简化电路模型

在本此应用中，制作在PCB上的线圈1和2的Q值一般能够到达50 250［4］。若驱动电源采用较低的输出阻抗的E类放大器实现，其Q值可较高。在本文采用的13.56 MHz的工作频率下，CMOS工艺可以实现未带负载时Q值为2的线圈［5］，而带负载时Q值更低，且随整流电路及其后功能电路工作状态变化，因此在0.1 1范围内考虑线圈4回路的Q值。

由于线圈1和2制作在同一PCB上，线圈3和4层叠集成在同一片上，它们的耦合系数k12、k34可以设计得较大。但是，由于线圈1和2在体外，线圈3和4在体内，相距较远且尺寸相差较大，因此它们之间的耦合系数远小于k12和k34。

由以上分析可得，hmn中h12远大于其他值，因此，式(3)的效率表达式可简化为:

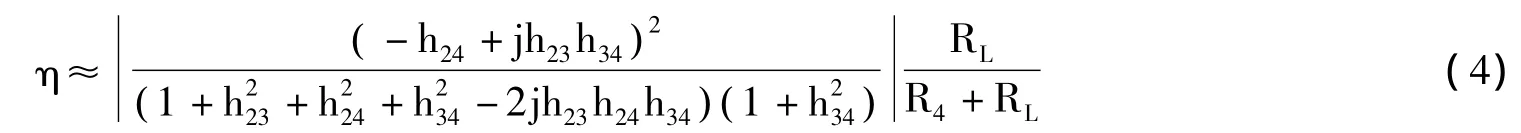
效率随Q4和k24变化时的结果如图2所示，其中图2(a)为简化模型式(4)的结果，图2(b)为完整模型式(3)的结果，其他参数分别为 Q1=Q2=100，Q3=2，k12=0.7，k13=k14=0.05，k23=k24，k34=0.7，RL≈R4+RL。从图2中可见，随着耦合系数k24和线圈4回路Q值Q4的增大，效率迅速增大，最大效率可达13%。同时，从图2中可见简化模型和完整模型之间的误差较小，具有较高的精度，为电路设计者提供较好的指导。

图2 效率随Q4和k24变化结果

2 与传统电感耦合无线电能传输比较

传统的电感耦合电能传输由两个线圈组成，这里将其记为体外线圈1和体内线圈4。当两个线圈工作于谐振方式时，可以达到最大效率［3］，此时的效率表达式为:

式中，k14作为体内外两个线圈之间的耦合系数，类似于磁耦合谐振方式中线圈2和线圈4之间的耦合系数k24。磁耦合谐振方式与传统电感耦合方式的传输效率在不同耦合系数k24和k14下，随Q4变化的比较结果如图3所示。其中，磁耦合谐振方式采用简化模型，各参数与图2所用相同;传统电感耦合方式参数Q1=100。

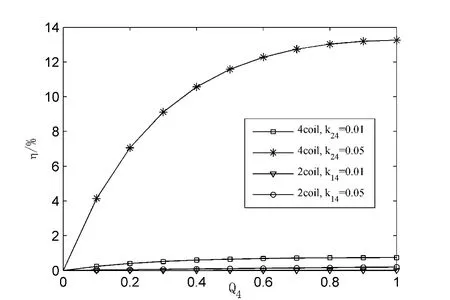
图3 磁耦合谐振方式与传统电感耦合方式传输效率比较

从图3中可见，磁耦合谐振方式的传输效率远大于传统电感耦合方式。这是由于传统电感耦合方式的h14值太小;而磁耦合谐振方式插入了线圈2和线圈3，分两步进行能量传输，且每一步的能量传输效率都较大:线圈2、3之间以及线圈3、4之间通过耦合系数和Q值的互相弥补实现了比直接从线圈2、线圈4耦合更高的传输效率。

3 结束语

本文针对植入式器件无线电能传输中，集成实现接收线圈的具体应用，分析了采用磁耦合谐振无线电能传输方式提高传输效率的可行性。建立了磁耦合谐振的完整电路理论模型及其简化模型，给电路设计者提供较好的指导作用。分析结果显示，与传统的电感耦合方式相比，磁耦合谐振方式具有更高的传输效率。

［1］Kurs A，Karalis A，Moffatt R，et al.Wireless power transfer via strongly coupled magnetic resonances［J］.Science，2007，317(5 834):83 －86.

［2］Haus H A，Huang W.Coupled-mode theory［J］.Proceedings of the IEEE，1991.79(10):1 505 －1 518.

［3］Kiani M，Ghovanloo M.The circuit theory behind coupled-mode magnetic resonance-based wireless power transmission［J］.IEEE Transaction on Circuits and Systems I:Regular Papers，2012，59(9):2 065 －2 074.

［4］Zargham M，Gulak P G.Maximum achievable efficiency in near-field coupled power－ transfer systems［J］.IEEE Transaction on Biomedical Circuits and Systems，2012，6(3):228 －245.

［5］Yue C P，Wong S S.Physical modeling of spiral inductors on silicon［J］.IEEE Transaction on Electron Devices，2000，47(3):560－568.