亲油多孔介质残余油膜的微观运移机理

谷建伟,张文静,张以根,黄迎松

(1.中国石油大学(华东)石油工程学院,山东 青岛 266580; 2.中国石化胜利油田分公司 地质科学研究院,山东 东营 063004)

亲油多孔介质残余油膜的微观运移机理

谷建伟1,张文静1,张以根2,黄迎松2

(1.中国石油大学(华东)石油工程学院,山东 青岛 266580; 2.中国石化胜利油田分公司 地质科学研究院,山东 东营 063004)

为研究亲油多孔介质中残余油膜的微观运移机理,以毛细管渗流模型为基础,结合边界层理论,建立膜状残余油微观渗流模型.根据亲油多孔介质中膜状残余油的分布特征,推导毛细管中油、水微观运移方程;改进毛细管模型,推导不等径毛细管模型的油水相对渗透率表达式,得到相对渗透率曲线,分析毛细管半径、边界层厚度和流体黏度对相对渗透率曲线的影响.结果表明:随着毛细管半径增大,相对渗透率曲线向左逐渐平移;随着边界层厚度减小,相对渗透率曲线向左逐渐平移;随着油黏度增大,水相的相对渗透率曲线向右下方逐渐平移,油相的相对渗透率曲线没有变化.该结果对分析高含水期残余油渗流机理及提高采收率提供理论指导.

亲油多孔介质;膜状残余油;边界层理论;微观运移;相对渗透率曲线

0 引言

对于注水开发油藏,水驱后的亲油岩石壁面上滞留大量原油吸附层,成为亲油孔隙中一类主要的残余油——油膜状残余油(简称膜状残余油)的存在形式,该吸附层即为原油边界层[1-6].低水淹部位存在较多膜状残余油[7],具有一定挖掘潜力.降低原油边界层厚度不仅能够增加原油的可采储量,而且能够增加油层的渗透率,改善原油在孔隙中的渗流特性[8].

边界层理论[9]由普朗特在1904年提出,对流体力学发展产生深远影响,近年来学者将它引入到油气田开发领域,开辟油气渗流研究的新方法.李中锋等通过实验发现原油边界层厚度与毛细管半径、压力梯度、流体黏度和组分的关系[10];刘卫东等以去离子水在微圆管中流动的实验数据为基础,通过数据拟合分析,确定流体流动速度、边界层厚度与压力梯度之间的关系[11].张普等通过实验发现,低渗多孔介质中流体的渗流特征受吸附边界层的影响极大,边界层越厚,渗流规律越偏离达西定律[12].

有关边界层理论的研究大多建立在实验基础上[4],对其与原油开采理论结合的研究较少.文中结合改进的毛细管渗流模型和边界层理论,建立膜状残余油微观渗流模型,推导不等径毛细管中油、水的微观运移方程,得出油、水相对渗透率表达式,为残余油开采提供理论依据.

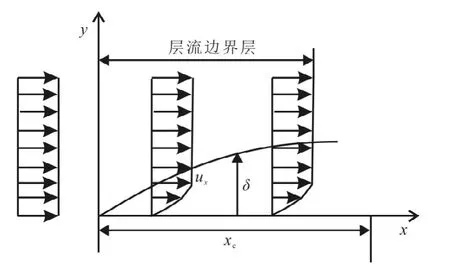
图1 平板壁面上层流边界层示意Fig.1 The formation of laminar boundary layer on flat surface

1 运动方程

膜状残余油运动模式可用边界层理论表述,边界层定义为紧贴壁面的一层极薄的流体,附着在壁面上不滑脱,流体的速度值为0.在壁面附近流体流动法向方向上,流体有较大的速度梯度,且受到黏滞力作用的影响,其平板壁面上层流边界层见图1,其中ux为边界层流体速度;xc为边界层临界距离;δ为边界层厚度.

假设:(1)毛细管中的流体呈层流流动;(2)原油边界层对称、均匀分布在毛细管壁内侧,毛细管中心为水的流动通道.膜状残余油微观渗流模型见图2,其中,r0为毛细管半径;p1、p2为毛细管两端压力;vo、vw为油、水相的流速;L为毛细管长度.

由图2可以看出:由于黏滞力的影响,油、水两相呈层流流动.把油、水两相的流动看成一组分别以不同速度运动、长度为L的同心液筒[13-15],有

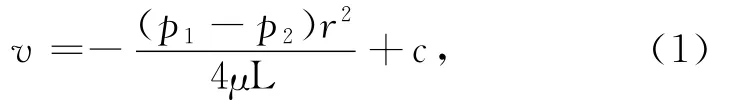
油、水两相的运动方程分别为

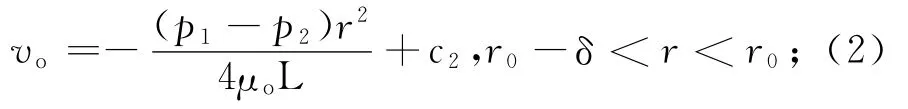
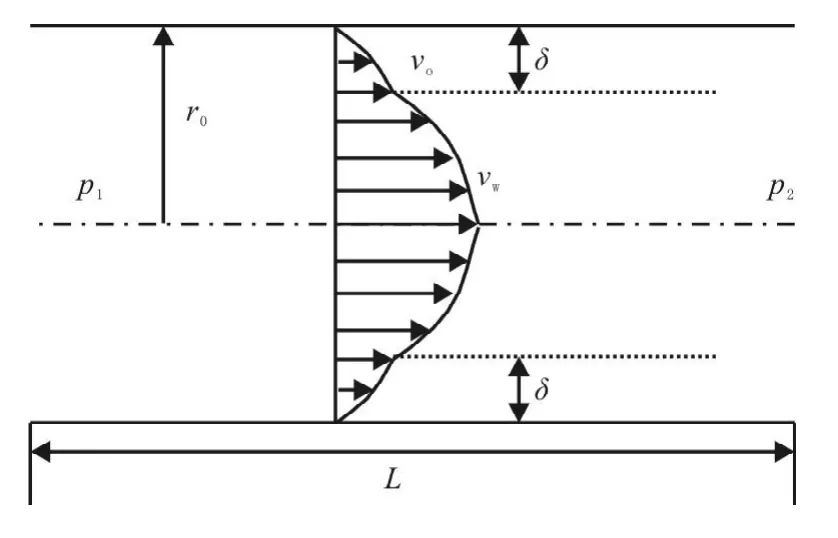
图2 膜状残余油微观渗流模型Fig.2 Microscopic seepage model of residual oil film

式(1-3)中:r为毛细管中心到任意位置的径向距离;μw、μo分别为水和油的黏度;c1、c2为常数.

边界条件为

根据式(4)边界层厚度定义,取vo为vw的99%时的δ值,即

将边界条件代入式(2)和(3),得

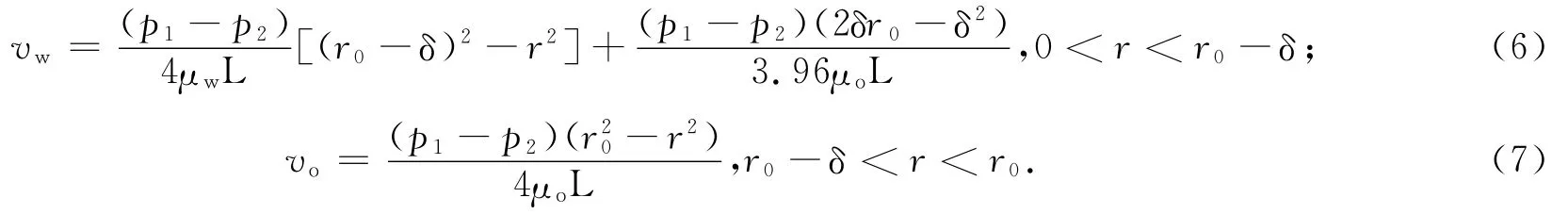
2 相对渗透率

假设岩石孔隙为由n根半径为ri(i=1,2,…,n)的毛细管构成的毛细管束,则真实岩石的孔隙体积Vp可以等价为由n根半径为ri(i=1,2,…,n)的不等径毛细管的体积,通过每根毛细管的油、水流量分别为

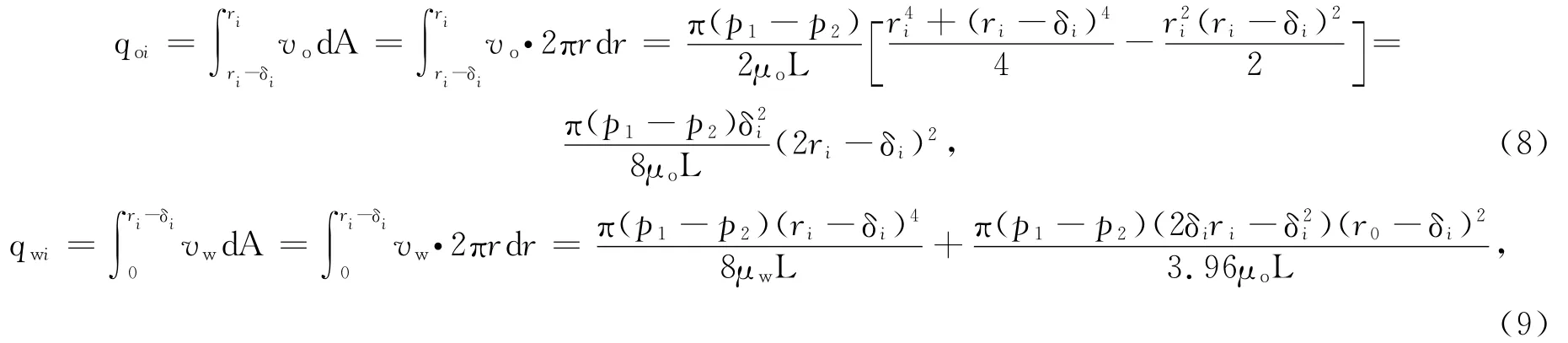
式(8-9)中:qoi、qwi分别为第i(i=1,2,…,n)根毛细管中的油、水流量;δi为第i根毛细管中的边界层厚度;A为同心液筒的柱筒面积,A=2πr L.

通过假设岩石的油、水总流量分别为

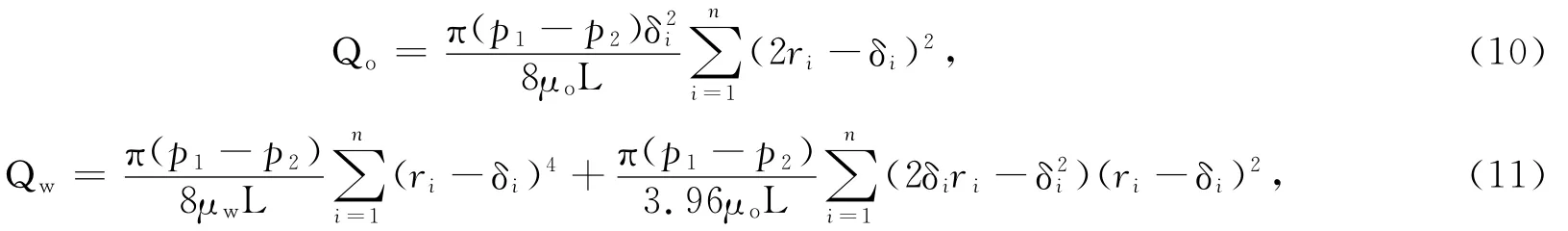
式(10-11)中:Qo、Qw分别为通过假想岩石的油、水总流量.

假设岩石的含水饱和度为

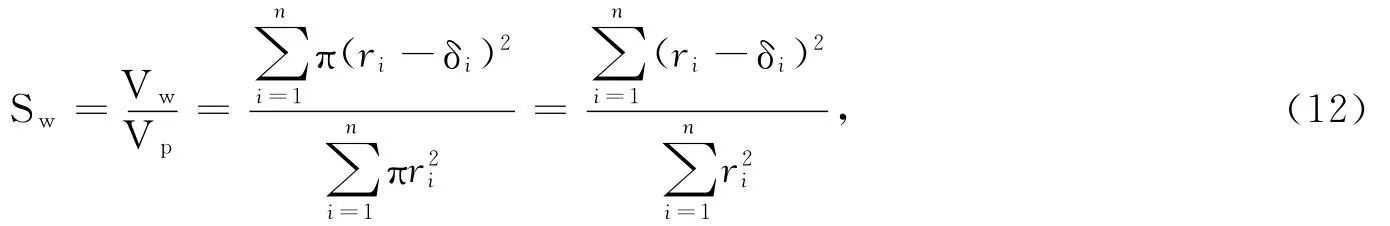
式中:Vw为假设岩石中水的体积;Vp为孔隙体积.

通过真实岩石的油、水流量为

式(13-14)中:Q′o、Q′w分别为通过真实岩石的油、水流量;Kro、Krw为油、水的相对渗透率.

联立式(10-12),可得

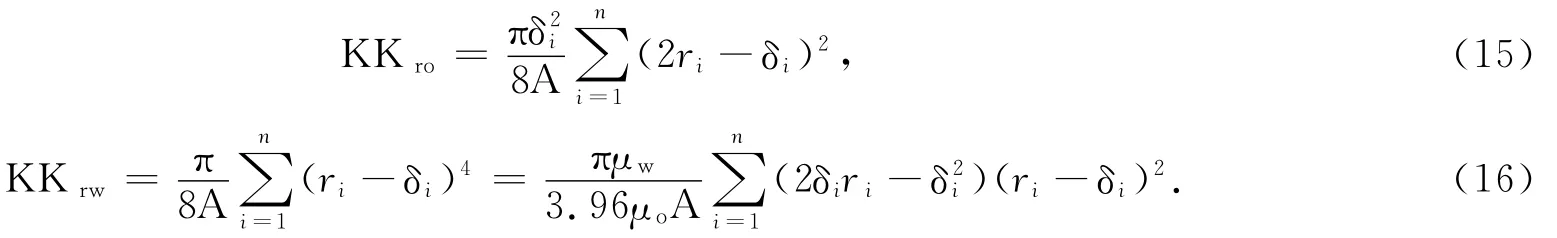
绝对渗透率表示为

联立式(15-17)得到油、水相对渗透率的表达式为

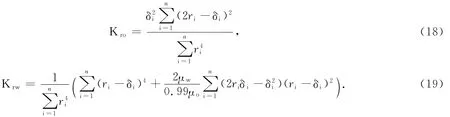
3 相对渗透率影响因素

根据文中推导的油、水相对渗透率公式,由式(12)得到毛细管束在不同边界层厚度下的含水饱和度,由式(18-19)得到不同含水饱和度下的油、水相相对渗透率,并绘制油、水相对渗透率曲线.

3.1 毛细管半径

毛细管半径对油、水相对渗透率的影响在真实岩石中对应岩石孔隙结构对油、水相对渗透率的影响.高渗、大孔隙、连通性好的岩心的油、水两相渗流区范围较大,而低渗、小孔隙、连通性差的岩心的正好相反.设毛细管根数n=1 000,毛细管半径的分布范围分别为0.05～50.00、15.05～65.00和25.05～75.00 μm,毛细管平均半径分别为25.03、40.03和50.03μm,不同毛细管半径下油、水相相对渗透率曲线见图3.

由图3可以看出:随着毛细管半径逐渐增大,油相相对渗透率降低,水相相对渗透率增大.因为边界层厚度与毛细管半径成反比,随着毛细管半径的增大,边界层变薄,油相所占的渗流通道变小,水相所占的渗流通道变大,所以油的渗流能力减小,水的渗流能力增大,表现在油、水相相对渗透率曲线上为曲线左移.

3.2 边界层厚度

边界层厚度对油、水相对渗透率的影响,实质上是油、水所占渗流通道的大小对油、水相对渗透率的影响.边界层厚度越大,油相所占的渗流通道越大,水相所占的渗流通道越小.因为边界层厚度与驱替时间和毛细管半径成反相关[12],所以设置边界层厚度与驱替时间,与毛细管半径成反比,毛细管根数依然为1 000,通过计算得到边界层平均厚度的分布范围分别为15.247 6～0.620 5、13.251 5～0.661 3和12.544 3～0.739 3μm,边界层平均厚度分别为2.132 6、2.137 3和2.270 1μm,不同边界层厚度下油、水相相对渗透率曲线见图4.

由图4可以看出:随着边界层厚度的减小,油、水相对渗透率曲线向左平移.因为随着边界层厚度的减小,越多的流动通道被水相占据,油的流动通道就越小,所以导致油的渗流能力减小,水的渗流能力增大,表现在相对渗透率曲线上为整个曲线左移.

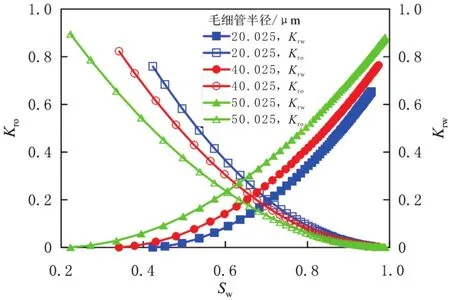
图3 不同毛细管半径下油、水相相对渗透率曲线Fig.3 Relative permeability curves under different capillary radius

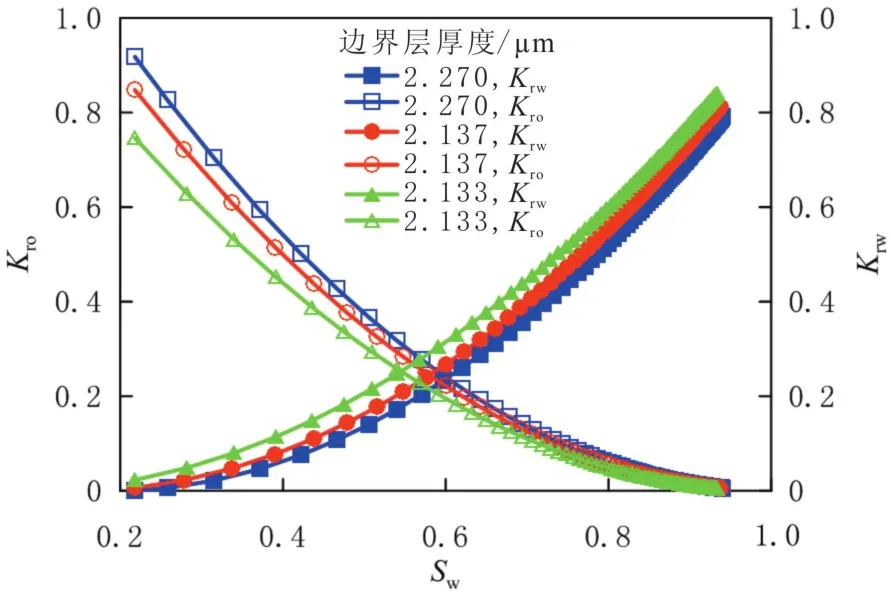
图4 不同边界层厚度下油、水相相对渗透率曲线Fig.4 Relative permeability curves under different boundary layer thickness

3.3 原油黏度

原油黏度对渗透率的影响存在不同观点:一种观点认为黏度对渗透率无影响;另一种观点认为当非润湿相黏度很高且远高于润湿相时,原油黏度对渗透率产生影响[13].设原油黏度分别为3、30和300 mPa·s,由式(18-19)计算不同原油黏度下油、水相相对渗透率曲线(见图5).

由图5可以看出:原油黏度对油、水相相对渗透率产生影响.随着原油黏度的增大,油相的相对渗透率曲线没有变化,水相的相对渗透率曲线向右下方平移.在油相占据的渗流通道不发生改变时,改变原油黏度对油相的渗透率的影响可以忽略;原油黏度越大,对油水边界处的水流动越不利,降低了水的相对渗透率;随着原油黏度的进一步增大,对油水边界处的影响越微弱.这表现在相对渗透率曲线上为水相相对渗透率曲线向右下方平移的趋势减弱.

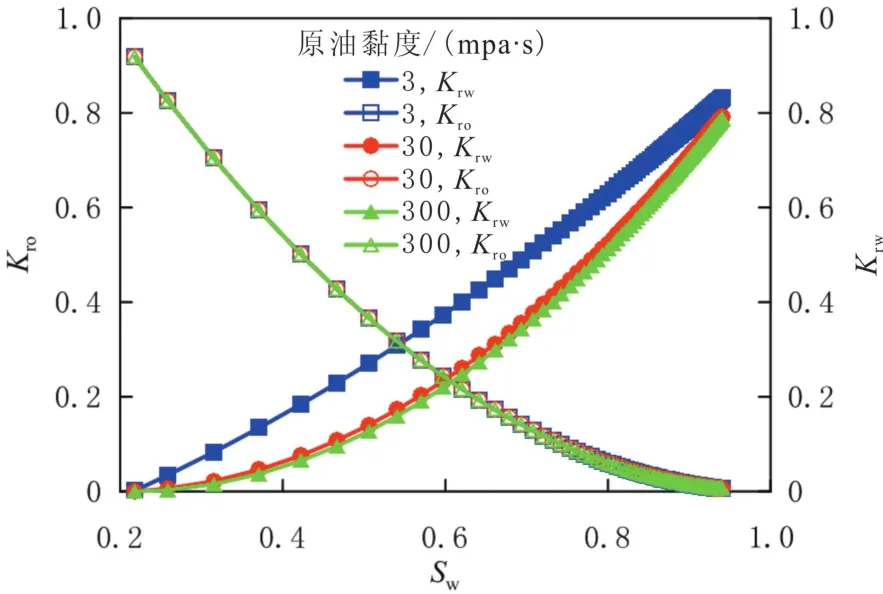
图5 不同原油黏度下油、水相相对渗透率曲线Fig.5 Relative permeability curves under different oil viscosity

4 结束语

运用边界层理论和毛细管渗流模型,研究亲油岩石孔隙中膜状残余油的微观渗流机理,建立不等径毛细管束模型渗流方程,并得到渗透率表达式,进一步得到油、水相对渗透率曲线.随着毛细管半径的增大,相对渗透率曲线向左平移;随着边界层厚度的减小,相对渗透率曲线向左平移;随着原油黏度增大,油相相对渗透率曲线没有变化,水相相对渗透率曲线向右下方平移.

[1] Hossein Nourozieh,Mohammad Kariznovi,Jalal Abedi,et al.A new approach to simulate the boundary layer in the vapour extraction process[J].Journal of Canadian Petroleum Technology,2011,50(11):11-18.

[2] Nadeem S,Anwar Hussain.Solutions for boundary layer flow in the region of the stagnation point towards a stretching sheet[J].Communications in Nonlinear Science and Numerical Simulation,2010,15(3):475-481.

[3] 王景灏,李菊香.流体层流横掠多孔介质中等温平板的边界层分析[J].大庆石油学院学报,2009,33(1):68-71.

Wang Jinghao,Li Juxiang.Boundary analysis of fluid's forced laminar flow over an isothermal plate in a porous medium[J].Journal of Daqing Petroleum Institute,2009,33(1):68-71.

[4] 刘慧枝,舒宏纪.边界层理论[M].北京:人民交通出版社,1991.

Liu Huizhi,Shu Hongji.Boundary layer theory[M].Beijing:China Communications Press,1991.

[5] 谢晓强,张蕾.不可压流体的边界层问题[J].数学年刊,2009,30A(3):309-332.

Xie Xiaoqiang,Zhang Lei.Boundary layer associated with incompressible Navier-Stokes equations[J].Annals of Mathematics,2009,30A(3):309-332.

[6] 姜瑞忠,杨仁峰.低渗透油藏非线性渗流理论与数值模拟技术[M].北京:石油工业出版社,2010.

Jiang Ruizhong,Yang Renfeng.Nonlinear seepage theory and numerical simulation technology in low permeability reservoirs[M].Beijing:Petroleum Industry Press,2010.

[7] 宋考平,杨钊,舒志华,等.聚合物驱剩余油微观分布的影响因素[J].大庆石油学院学报,2004,28(2):25-27.

Song Kaoping,Yang Zhao,Shu Zhihua,et al.Effective factors of microscopic distribution of remaining oil of polymer flooding[J].Journal of Daqing Petroleum Institute,2004,28(2):25-27.

[8] 张立娟,岳湘安.亲油岩石壁面残余油膜的微观驱替机理[J].油气地质与采收率,2007,14(1):79-82.

Zhang Lijuan,Yue Xiang'an.Microscopic displacement mechanism of oil segment remained on hydrophobic rock wall[J].PGRE,2007,14(1):79-82.

[9] Schlichting H.Boundary-layer theory[M].New York:McGraw-Hill,1968.

[10] 李中锋,何顺利.低渗透储层原油边界层对渗流规律的影响[J].大庆石油地质与开发,2005,24(2):57-59.

Li Zhongfeng,He Shunli.Influence of boundary layers upon filtration law in low-permeability oil reservoirs[J].Petroleum Geology&Oil field Development in Daqing,2005,24(2):57-59.

[11] 刘卫东,刘吉,孙灵辉,等.流体边界层对低渗透油藏渗流特征的影响[J].科技导报,2011,29(22):42-44.

Liu Weidong,Liu Ji,Sun Linghui,et al.Influence of fluid boundary layer on fluid flow in low permeability oilfield[J].Science&Technology,2011,29(22):42-44.

[12] 张普,张连忠,李文耀,等.边界层对低渗透非达西渗流规律影响的实验研究[J].河北工程大学学报:自然科学版,2008,25(3):70-72.

Zhang Pu,Zhang Lianzhong,Li Wenyao,et al.Experiment on the influence of boundary layer on the Non-Darcy seepage law[J].Journal of Hebei University of Engineering:Natural Science Edition,2008,25(3):70-72.

[13] 秦积舜,李爱芬.油层物理学[M].东营:中国石油大学出版社,2003.

Qin Jishun,Li Aifen.Reservoir physics[M].Dongying:China University of Petroleum Press,2003.

[14] 梁利平,姬定成,王光耀,等.基于毛细管的水驱剩余油模型[J].西北大学学报:自然科学版,2011,41(6):1025-1030.

Liang Liping,Ji Dingcheng,Wang Guangyao,et al.Remaining oil model of water flooding base on capillary[J].Journal of Northwest University:Natural Science Edition,2011,41(6):1025-1030.

[15] 谢刚.毛细管束流变模型内壁黏附力的测量及影响因素研究[J].黑龙江大学自然科学学报,2005,22(1):53-55.

Xie Gang.Measurement of the adhesive force at the internal wall of a capillary rheological model and its affecting factors[J].Journal of Natural Science of Heilongjiang University,2005,22(1):53-55.

TE341

A

2095- 4107(2014)01- 0080- 05

DOI 10.3969/j.issn.2095-4107.2014.01.012

2013- 11- 14;编辑:张兆虹

国家油气重大专项(2011ZX05011-002)

谷建伟(1971-),男,博士,教授,主要从事油藏工程方面的研究.