基于多尺度块搜索的单幅图像超分辨率重建
申世闻,曹 国,孙权森
(南京理工大学计算机科学与技术学院,南京 210014)
1 概述
图像超分辨率技术可以分为2个方向:基于重建的超分辨率技术[1-2]和基于学习的超分辨率技术[3-4]。基于重建的超分辨率技术利用多幅具有互补信息的低分辨率图像来复原其对应的高 /低分辨率图像[5],这些互补信息可以是亚像素差,也可以是不同的模糊核;此方法存在很多问题,如当放大倍数过大时(2倍以上),会因重建过程中能够使用的互补信息太少,导致重建效果不太理想[6]。基于学习的超分辨率技术基本思想为通过对高/低分辨率图像库的学习,在某种最优化方法下求出给定低分辨率图像对应高分辨率图像。如Freeman的方法[3]:运用马尔科夫网络找出对应的高分辨率块的最大后验概率值,在此基础上也有一系列改进方法[1,7]。以上这些方法都需要大量的训练集图像,且重建出的图像有明显的伪边缘,看起来十分不自然。重建速度过慢也是这类方法一个共同的缺陷。针对上述问题,如何在无任何先验信息的前提下,能够快速地对一张图像进行超分辨率重建,且重建效果良好,成了本文研究的问题。
本文在文献[8]的研究基础上做了3点改进:(1)把查找到的2个相似低分辨率块之间的差值进行插值放大,并加到对应的高分辨率块上。避免了低分辨率相似块之间差异较小,但是两者对应的高分辨率块却差异较大的情况。(2)不仅考虑到要重建的低分辨率和学习到的相似低分辨率之间的差异,而且考虑到重建出的高分辨率块是否和其周围的高分辨率块兼容。由于文献[8]并没有考虑这几点,使得其重建后的高分辨率图像有一定的锯齿现象,并且图像看起来极其不自然。(3)引入最新的随机块搜索[9]算法,使得算法用于KNN查找的速度大幅提高,降低了重建时间。
2 基于学习的超分辨率技术
在自然图像中,一副图像中像素块相似甚至相同的现象也较为普遍。文献[8]在伯克利分割数据库上做了大量的实验,并对结果进行了统计。实验证明源图像上多于90%的5×5小块,在此图像的其他位置都可以找到9个或者更多的相似块,大约80%的图像块在源图像的0.41=1.25–4下采样级别上有9或者更多的相似块,大约70%的图像块在源图像的0.26=1.25–6下采样级别上有9或者更多的相似块。这一结论奠定了利用一幅图像及其下采样图像的块冗余信息进行高分辨率重建的基础。文献[8]把基于重建和基于学习的超分辨率方法结合起来,利用不同级的相似块,构成对应的高/低分辨率块集,通过学习找出低分辨率块对应的多个中间级的高分辨率块。把这多个中间级高分辨率看成具有互补信息的冗余块,最终用这些互补信息来复原目标级高分辨率块。
2.1 高低分辨率图像间的线性约束
现给定一幅低分辨率图像L,假定它是由原高分辨率图像H经过模糊和下采样过程得到:L=(H*B)↓s。这里,↓代表下采样操作;s是H和L之间下采样的缩小比例因子;B是相应的模糊核(点扩散方程);*为卷积。因此,L中的每个像素p的值可由高分辨率图像相应位置上像素q∈H及其周围的像素进行线性变换求得,有:
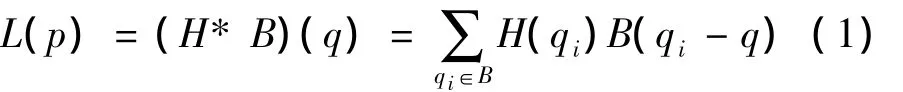
这里用高斯核对B进行估计,i的大小由模糊核B来决定。如果有足够多的低分辨率图像,就形成了上述方程的方程组,并且如果独立方程的个数大于未知数的个数,则方程(1)有解。正如文献[8]所述,一幅图像本身及其下采样图像中有大量的冗余块。设P为低分辨率图像L中以p为中心的一个5×5图像块,L中存在多个相似图像块 P1,P2,…,Pk(在L下采样中也可找到多个相似块)。假设这k个低分辨率块来自于k个不同低分辨率图像,且这些低分辨率图像描述的是同一个高分辨率场景。可利用传统的多帧超分辨率重建方法进行亚像素配准[2],并根据P和Pi之间的相似度对相应方程的可信度进行衡量,最终解出目标高分辨率H。
2.2 不同分辨率图像级联中的块冗余
现在令I0,I1,…,In为从低分辨率L到目标高分辨率H的级联,且分辨率依次递增(即I0=I,In=H)。相应的模糊核为 B0,B1,…,Bn(点扩散函数),这样每一个Il满足L=(Il*Bl)↓sl(sl表示相应的放缩因子)。仍然用高斯核来代替,方差由 sl决定。放缩因子sl用sl=αl表示,这里α为相邻级之间的放大倍数。
为了得到各级中间图像Il,可以分下面3个步骤。
(1)建库:为每级图像建立低/高分辨率库[P,Q]l。设 L=I0,I-1,…,I-m为从 L 开始分辨率逐渐降低的一组级联,这些低分辨率图像可以由L进行模糊下采样得到 I-l=(L*B-l)↓sl,B-l=Bl。为 I-l中每个点取以其为中心的块,并在 I0中取相应位置 sl·∈I0上的块 Q0(sl·),这样就构成了低高图像块库在后面的实验中,取低分辨率块大小为5×5,若放大2倍sl=2,则高分辨率块大小为9×9。有些文献中用其他形式特征来建库,如拉普拉斯金字塔[7]、梯度特征[4]。
(2)相似块查找:在库中搜索和P0(p)相似的低分辨率块,文献[8]里面用到了近似最近邻查找算法(k=9)[10]。

图1 高分辨率块学习过程
2.3 随机最近邻查找算法的引入
由前文可知,求相似块是一个极其重要的步骤。但由于源图像块与各级下采样块数目过多,想要准确地查找到k个近邻需要花费大量的时间。例如用最普通的查找算法需耗时O(r2M),其中,r为块大小;M为图像中的像素数。故基于学习的超分辨率方法一般选用近似最近临查找法。这些方法基本上是基于树结构的,如 TSVQ[11],kd-trees[12]和 VP-trees[13],这些方法都是利用块的维数进行查找。并且经常和降维技术结合起来使用,如PCA[12]。能够达到耗时O(mMlogM),但是建树时需多增加O(M)的内存空间,这里m为树的维数。
但是基于树的查找方法在建树和查找上面仍然花费大量时间,它并没有考虑到图像具有局部相似性。为此,本文引入了Connelly的随机块匹配算法[10],此算法在时间和空间消耗上面都要优于带降维的kd-trees。它几乎不需要额外的空间消耗,仍需耗时O(mMlogM)。虽然在数量级上和最右的基于树结构的查找算法相同,但是实际上的常数要远小于基于树结果的查找算法。由于本文的着重点并不在求随机最近邻这一步骤,因此该方法的详细步骤在此不予列出。此方法也有一定的局限性,只能用于如图像这类具有局部相似性的搜索,并且实验结果也受到实验环境的影响(并行计算)。
3 目标图像的重建
本文对上KNN查找到了中间级高分辨率块做了改进,并且在用这些中间级高分辨率块复原目标级高分辨图像时考虑到多方面因素。本文通过自适应加权使得重建结果模糊度和锯齿现象都有所降低,看起来更自然。
3.1 高分辨率块的改进
虽然P1,P2,…,P9和P之间较为近似,但是不同Pi对应的高分辨率块Qi之间却差别很大[3],这也是由文献[8]重建出的图像看起来不自然的一个原因。并不直接使用学习出的Qi作为P对应的高分辨率估计值。本文把P与Pi之间的差值进行放大(可采用双立方法),再加到对应的高分辨率Qi上面,使得到的高分辨率估计值更加准确,如图2所示。

图2 修正学习到的高分辨率Qi
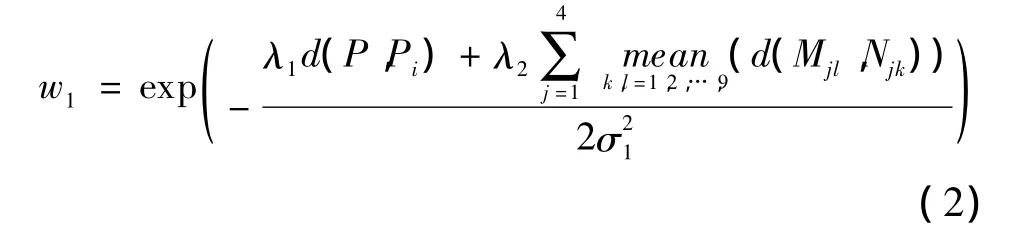
其中,σ1为高斯核的标准差;λ1,λ2为系数;w1不仅考虑到了由于相似度不同导致的9个相似块的可信度不同,而且考虑到了相邻块重叠部分的相似度对重建结果的影响,这样不仅使得重建出的目标分辨率H和真实的高分辨率图像更吻合,而且大大消除了锯齿现象,使得重建效果看起来更真实。σ1的取值也对最终的放大效果有着重要影响,关系到最终图像的清晰度。
3.2 不同权值下数值的求解
并不是由式(1)直接求出 H,而是依次把 I1,I2,…,Il当成目标高分辨率,每级都要求出直到H。当把 Il+1当作目标分辨率进行重建时(此时I1,I2,…,Il已求出),同时利用2.1节在L上找到了多个低分辨率块P1,P2,…,Pk和2.2节中以 L为中间级学习到的多级(1,2,…,l+1)高分辨率块(也可以Ii,i≤l为中间级,学习出 i+1,i+2,…,l级的高分辨率块)。通过块加权分别把每级高分辨块拼接融合成一幅高分辨率图像。

当求出图像Il+1时,再通过相同的模糊和下采样求出和L一样大小的低分辨率图像,并和L比较。差距的大小预示着求出的高分辨率图像Il+1和真实图像之间的差距。可以用“反投影”法[5]来修正求出的高分辨率图像,此过程和图2类似。这一步骤确保每个新得到的高分辨率图像Il+1和输入的低分辨率图像L一致。
4 实验结果及分析
本文从有参图像质量评价和无参图像质量评价2个方面进行比较。有参质量评价所用的20张灰度图片来自Granada大学计算机视觉组数据库。包括自然图像,如人像、风景、建筑、静物、显微镜图像、合成图像以及遥感图像。每张图像的大小都是512×512像素。实验操作平台硬件为Intel Core i5-2450 MB、2.5 GHz、4 核心、3 GB 内存,软件配置为Windows 7 旗舰版32位操作系统,Matlab R2009a。
4.1 随机查找算法效率比较
本文采用的随机查找算法[9],在相同的配置下和文献[8]中所用到的 kd-tree[10]和 priority-kdtree[10]算法进行比较。以2个相似块差值的加权平方和作为块与块之间的距离,权值大小和式(3)相同。查找时间以秒为单位,比较结果如表1所示。表中第1行为在源图像中查找相似块。

表1 各种搜索方法的对比
本文通过调节参数使块与块的平均距离尽可能相同,可以看出随机查找算法在块与块的平均距离略小的情况下,速度提高了近2倍。表1中第2行为在源图像的下采样图像中查找的实验结果,实验时先对源图像进行模糊加高斯白噪声,下采样率为0.5。而且还发现当近邻k的数量增加时,此算法要更优于树结构的算法。
4.2 重建图像质量比较
将本文改进的块查找算法运用在图像超分辨率放大上面,对高分辨率图像进行模糊、加高斯白噪声,并进行下采样得到128×128像素的低分辨率图像,图像的质量相对较差。用本文方法放大4倍并和最近邻插值、双线性插值、双立方法比较,实验结果如表2所示。
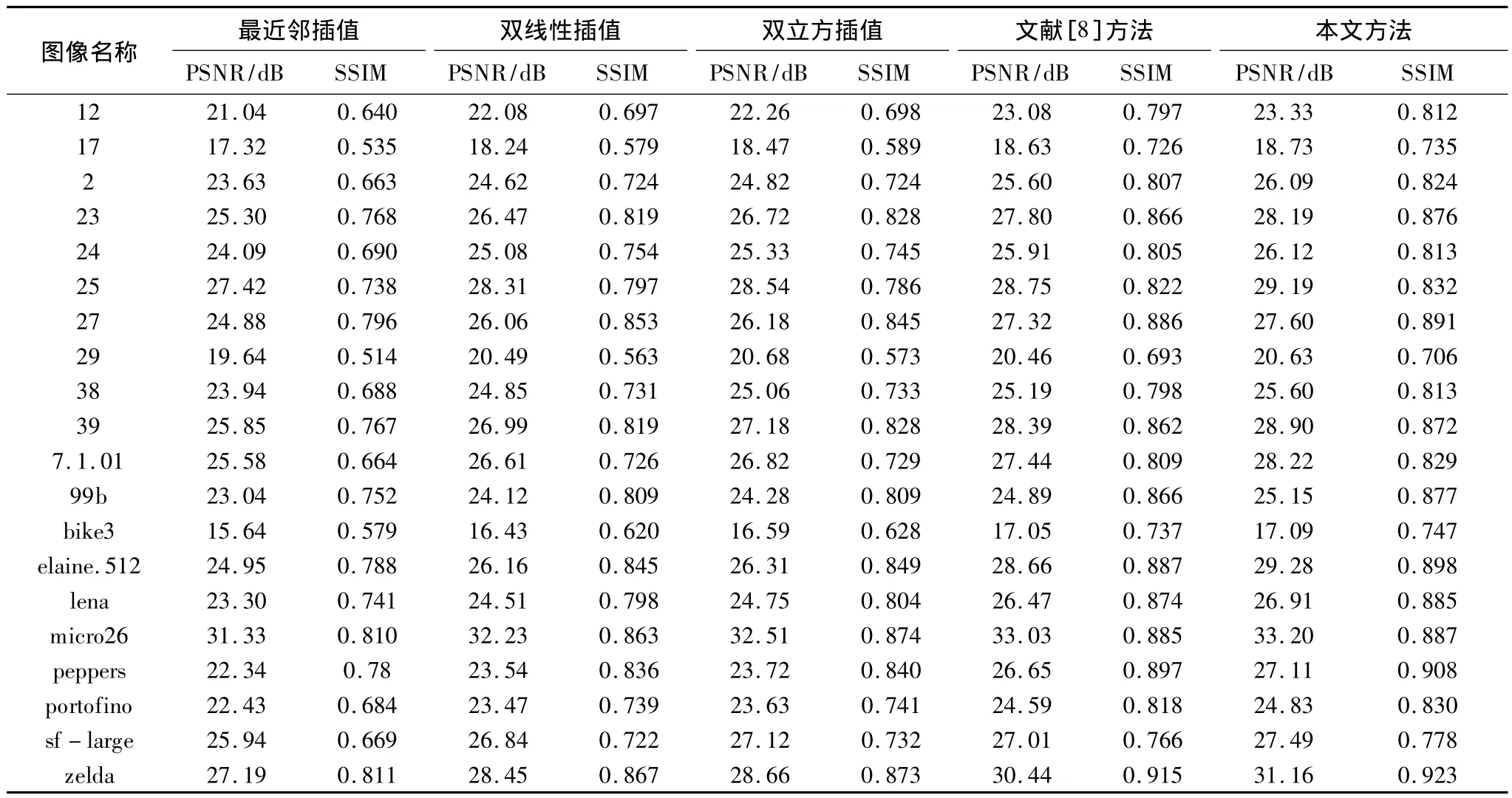
表2 各方法放大结果比较
大量实验结果表明,随着σ1的增大图像会更加模糊。若源图像质量较差时σ1应取值较大值(如180),但是和双立方法的实验结果比较时还是要明显清晰很多;当源图像较好时,σ1应取值较小值(如20)。实验中取 λ1=0.5,λ2=0.05。由于低分辨率图像质量较差且放大倍数较高,其他方法都显示出了其本身固有的缺点,而本文方法要明显好于其他方法。前文的3个方法都是利用Matlab的imresize函数来完成的。本文选择2个指标:峰值信噪比(Peak Signal to Noise Ratio,PSNR)和结构相似性(Structural Similarity,SSIM)来衡量算法的好坏。
表2的结果是有参的质量评价,可以看出无论文献[8]方法还是本文方法,和传统的插值方法比较都有着很明显的优势。另外本文方法从多幅图像重建结果看,都要好于文献[8]方法的结果。
为了进一步进行对比,本文和文献[8]中一样也采用Berkeley大学视觉组的彩色图像进行实验。这些图片相对于前文选择的20张灰度图像,图像质量好且清晰度高。下面将从无参的客观评价和主观评价2个方面对实验结果进行对比。
选用文献[15]的方法作为无参的客观评价标准,此方法从模糊度以及锯齿性等多个方面来衡量图像的好坏。分值越低,图像的质量越优。结果和人视觉系统判断效果较为吻合。先把RGB图像转换为 YCbCr值,再用本文方法放大4倍并和文献[8]的放大结果进行比较,实验结果如表3所示。图3、图4为重建效果,从视觉上可以看出本文方法明显优于其他方法,比双立方法更加清晰,减少了边缘模糊。通过对细节的放大可以看出,相比于文献[8]方法锯齿现象有所减少,图像看起来更自然。特别是图3中帽子和孩子脸部分、图4中花瓣边缘和蝴蝶翅膀边缘,要明显好于文献[8]方法。图像放大4倍后仍有很好的效果。

表3 无参图像质量评价结果

图3 重建效果1

图4 重建效果2
5 结束语
本文利用多尺度图像之间的块冗余现象,提出了一种快速超分辨率重建的方法。已有的超分辨率方法多侧重利用不同的信息(如高频、低频)来建立高低分辨率库,而鲜有对查找到的相似块进行修正以及对图像块进行更准确的加权的,并且速度较慢。本文依据这一思路对算法做了改进。实验证明本文算法无论是重建速度还是重建图像质量都有所提高。下一步工作是结合基于学习的超分辨率重建算法与传统的基于重建的超分辨率算法作进一步研究。
[1]Tsai R Y,Huang T S.Multipleframe Image Restoration and Registration[C]//Proc.of Conference on Advances in Computer Vision and Image Processing.Greenwich,USA:JAI Press Inc.,1984:317-339.
[2]Stark H,Oskoui P.High-resolution Image Recovery from Image-plane Arrays,Using Convex Projections[J].Journal of the Optical Society of America A,1989,6(11):1715-1726.
[3]Freeman W T,Jones T R,Pasztor E C.Example-based Super-resolution[J].IEEE Computer Graphics and Applications,2002,22(2):56-65.
[4]Chang Hong,Yeung D Y,Xiong Yimin.Super-resolution Through Neighbor Embedding[C]//Proc.of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington D.C.,USA:[s.n.],2004:275-282.
[5]Irani M,Peleg S.Improving Resolution by Image Registration[J].CVGIP:Graphical Models and Image Processing,1991,53(3):231-239.
[6]Baker S,Kanade T.Limits on Super-resolution and How to Break Them[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(9):1167-1183.
[7]薛翠红,于 明,于 洋,等.基于MAP框架的金字塔人脸超分辨率算法[J].计算机工程,2012,38(10):206-208.
[8]Glasner D,Bagon S,Irani M.Super-resolution from a Single Image[C]//Proc.of the 12th International Conference on Computer Vision.Kyoto,Japan:[s.n.],2009:349-356.
[9]Barnes C,ShechtmanE,GoldmanD B,etal.The Generalized Patch Match Correspondence Algorithm[C]//Proc.of the 11th European Conference on Computer Vision.Heraklion,Greece:[s.n.],2010:29-43.
[10]Arya S,Mount D M.Approximate Nearest Neighbor Queries in Fixed Dimensions[C]//Proc.of the 4th Annual ACMSIAM Symposium on Discrete Algorithms.Philadelphia,USA:[s.n.],1993:271-280.
[11]Wei Liyi,Levoy M.Fast Texture Synthesis Using Tree Structured Vector Quantization[C]//Proc.of the 27th Annual Conference on Computer Graphics and Interactive Techniques.New Orleans,USA:ACM Press,2000:479-488.
[12]Hertzmann A,Jacobs C E,Oliver N,et al.Image Analogies[C]//Proc.of the 28th Annual Conference on Computer Graphics and Interactive Techniques.Los Angeles,California,USA:[s.n.],2001:327-340.
[13]Kumar N,Zhang Li,Nayar S.What is a Good Nearest Neighbors Algorithm for Finding Similar Patches in Images?[C]//Proc.of the 10th European Conference on Computer Vision.Berlin,Germany:[s.n.],2008:364-378.
[14]姚 琦,沈 松,朱 飞.基于加权 POCS的图像超分辨率重建[J].计算机工程,2013,39(3):264-266,271.
[15]Mittal A,Soundararajan R,Bovik A.Making a“Completely Blind” Image Quality Analyzer[J].IEEE Transactions on Signal Processing Letters,2013,20(3):209-212.

