小波变换与GARCH组合模型的网络流量预测＊

刘 渊，黄世忠

（江南大学数字媒体学院，江苏 无锡 214211）

1 引言

随着各种网络服务如网上支付、视频会议、IP电话等的广泛应用，人们对网络质量的要求越来越高。然而，当今网络已经变得十分复杂，出现突发事件与拥塞的可能性也大为增加，因此改善网络的运行环境显得至关重要，这就需要人们更好地了解网络流量的特征及其变化规律并用来预测未来的网络流量。网络流量预测在拥塞控制、网络管理与诊断、路由器设计等领域都具有重要意义［1］。

近年来，许多学者应用小波变换和时间序列方法对网络流量进行了大量的研究和分析。文献［2］在国内最早提出了基于小波的多尺度网络流量自回归滑动平均ARMA（Auto Regressive Moving Average）预测模型。该模型融合了多尺度时间序列分析和回归分析的优点，在网络流量预测中得到了广泛应用。但是，由于其基于线性建模并且假设网络流量序列为同方差，因此在某些环境中，难以准确、全面地描述网络流量的非线性变化规律，从而影响最终预测精度［3］。

Engel［4］首先提出了广义自回归条件异方差GARCH（Generalized Auto Regressive Conditional Heteroskedasticity）模型，用于对时间序列的方差进行建模。GARCH模型可以较好地描述序列的异方差性，因此在时间序列建模和预测中具有广泛应用。

在一些网络环境中，网络流量数据存在波动聚类性和异方差性，而国内将GARCH模型应用于网络流量预测的文献极少，因此本文提出使用小波变换与GARCH的组合模型进行网络流量预测。

2 基本理论

2.1 小波变换

小波变换［5］是一个平方可积函数f（t）与一个在时频域上均具有良好局部性质的小波函数φ（t）的内积：

其中，〈＊，＊〉表示内积，a＞0为尺度因子，b为位移因子，＊表示复数共轭，φa，b（t）称为小波。

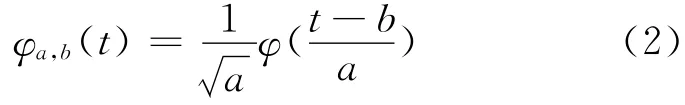
改变a值，对函数φa，b（t）具有伸展（a＞1）或收缩（a＜1）的作用；改变b值，则会影响函数f（t）围绕b点的分析结果。φ（t）称为母小波函数，其必须满足容许性条件：

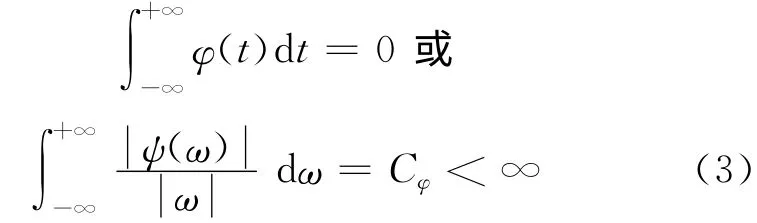
其中，φ（t）是ψ（ω）的傅里叶变换。

在实际应用中，需要对尺度因子a和位移因子b进行离散化处理，可以取：

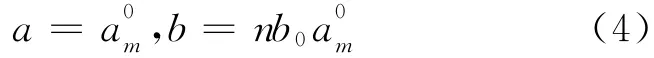
其中，m、n为整数，b0为大于1的常数，a和b的选取与小波φ（t）的具体形式有关。

则离散小波函数表示为：

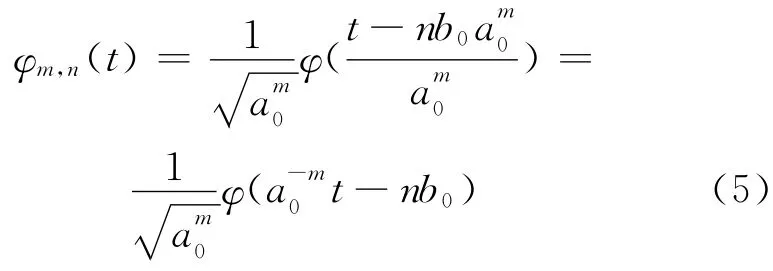
相应的离散小波变换表示为：

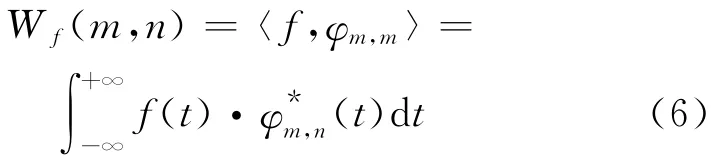
二进制离散小波变换Mallat算法简洁实用，广泛应用于实际时间序列处理中。

Mallat小波分解是将原始信号分别通过高频和低频两个滤波器进行频带划分，该算法可表示为：

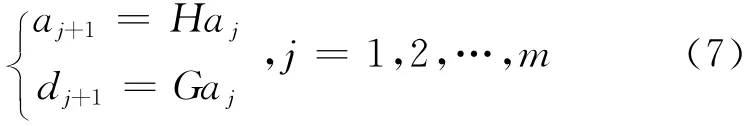
其中，H为低通滤波器，G为高通滤波器。Mallat算法将原始信号分解为低频部分和高频部分。低频部分是近似分量，反映的是信号的轮廓特征与变化趋势；高频部分是细节分量，反映随机扰动等动态因素所带来的影响。

分解后的信号可由Mallat重构算法进行重构，该算法可表示为：

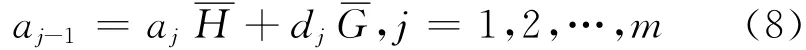
其中，和分别为H和G的对偶算子。

2.2 GARCH模型

GARCH模 型［6，7］是 自 回 归 条 件 异 方 差 模 型ARCH（Auto Regressive Conditional Heteroskedasticity）模型的进一步推广，其定义如下：对于给定的阶数p≥0和q≥0，有：

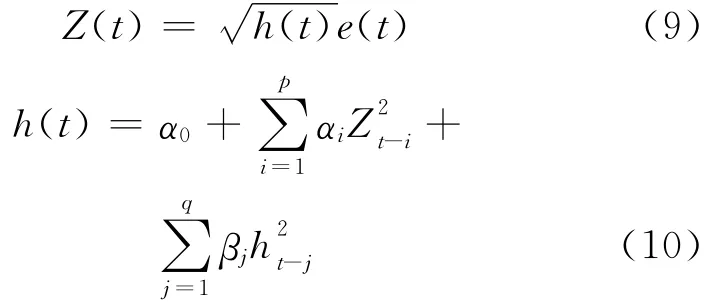
其中，e（t）～IID（0，1），也就是说，｛e（t）｝是一个均值为0、方差为1的独立同分布随机变量序列，并且e（t）与过去的值无关。e（t）与Zt－k（k≥1）相互独立，α0＞1，αi≥0，β≥0均为常数，且满足：

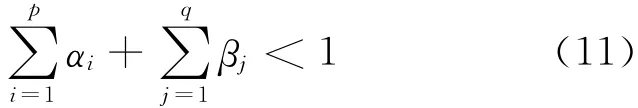
式（10）定 义 的 随 机 过 程z（t）称 为GARCH（p，q）过程。其中，h（t）是z（t）的条件变量，对于｛Z（s），s＜t｝，e（t）为相应的残差变量。GARCH模型的实质是使用残差平方序列的q阶滑动平均拟合当期异方差函数值以及利用异方差函数的p阶自相关性。

3 仿真实验

3.1 实验说明

本文采用实际流量数据LBL－tcp－3.tcp［7］进行网络流量预测实验。该数据集来源于伯克利实验室，是公允的权威流量数据。其内容包括两小时内在一个隔离区（Demilitarized Zone）中通过某服务器所有的网络流量数据，以微秒级记录某个时刻的网络数据流量大小。

通过计算，本文以1秒为时间尺度获得了该网络中前2 000秒的网络数据流量（如图1所示），并使用前1 900秒的网络流量数据进行小波分解，将其分解成高频信号和低频信号，如果这些分量信号存在GARCH效应，则进行GARCH建模；如不存在GARCH效应，则进行ARMA建模。然后，分别使用这些模型预测后100秒的网络流量，最终通过小波分析理论将预测的结果进行重构，并与真实流量数据进行比较并计算出精确度的量化指标。

为了达到对比目的，本文使用了传统的小波分析与ARMA组合模型对相同的网络流量数据建模和预测，并将其预测结果与小波分析与GARCH组合模型预测结果进行比较。

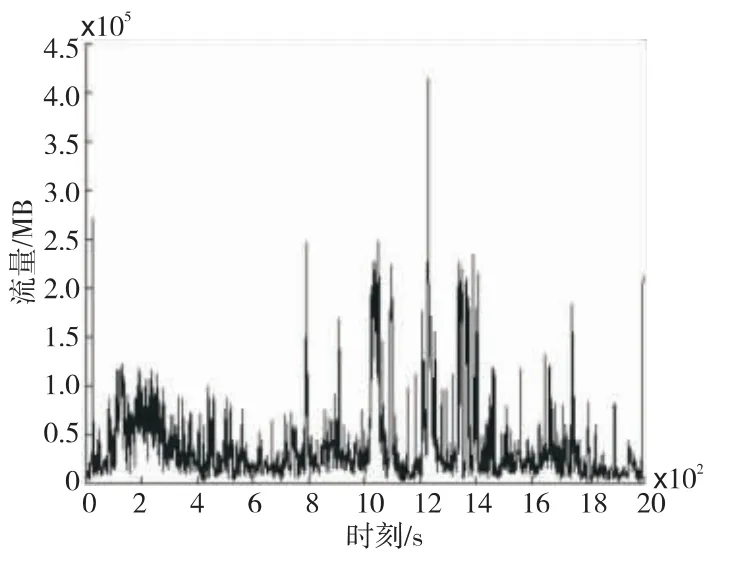
Figure 1 Experimental network traffic data图1 实验网络流量数据

3.2 小波分解

本文运用了Daubechies（db3）小波，使用Mallat算法对实验数据进行尺度为w的小波分解，得到一组近似分量aw和w组细节分量dj（j＝1，2，…，w）。w值的选取不宜过大，也不宜过小。w过大对流量数据的信息损失大，分解过程中必然存在计算上的误差；w过小则不能很好地得到反映流量数据某些特性的高频信号。通过反复实验，当w＝3时误差较小且能获取丰富的高频信号，结果如图2所示。

3.3 建模与预测

对各子序列a3，d3，d2，d1建立起合适的模型。通过拉格朗日乘数检验方法［8］得出子序列d2和d1具有GARCH效应，因此对子序列d2和d1建立GARCH模型，对a3和d3则建立ARMA模型。

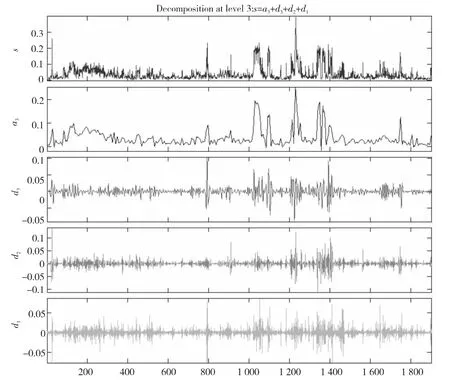
Figure 2 3－level wavelet decomposition of the raw network traffic图2 db3小波对原始网络流量进行三层分解

本文限于篇幅，仅介绍子序列d2的GARCH建模过程。

为了选择合适的GARCH阶数，本节计算了赤池信息量准则AIC（Akaike Information Criterion）［9］值。AIC准则要求AIC值越小越好，其计算结果如表1所示。

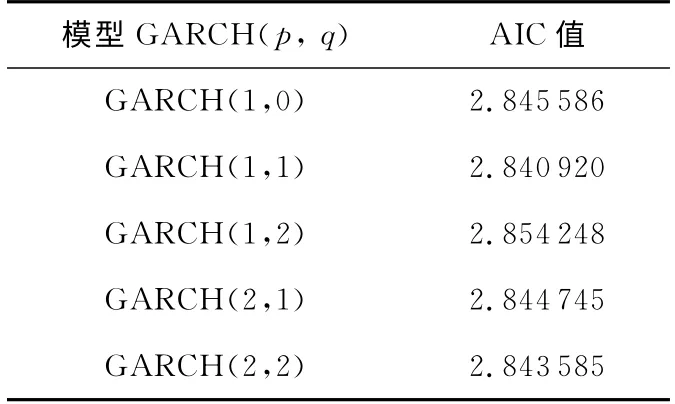
Table 1 AIC of subsequence d2of GARCH with different orders表1 子序列d2的GARCH模型阶数的AIC值

综上，GARCH（1，1）的AIC值最小，因此选择GARCH（1，1）较为合适。

然后，使用极大似然估计，计算出该模型的各参数的估计值，其结果如表2所示。

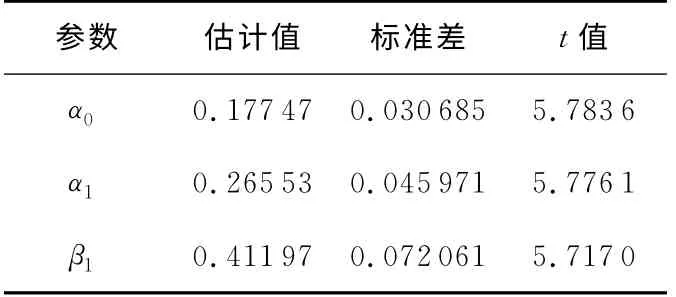
Table 2 Parameters estimation of GARCH（1，1）表2 GARCH（1，1）模型的参数估计

接着就可以使用该GARCH（1，1）模型来预测子序列d2后100秒的数据。

3.4 预测结果及其对比

使用Mallat重构算法，将子序列a3，d3，d2，d1的预测结果进行重构，最终便可得到原始流量序列的预测值。

为了对预测效果进行客观的量化评价，本节引入了式（12）和式（13）量化指标。

均方根误差（RMSE）：

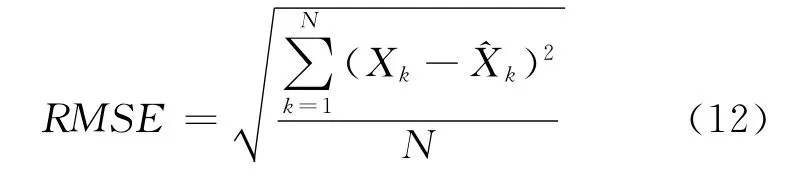
相对均方根误差（RRMSE）：

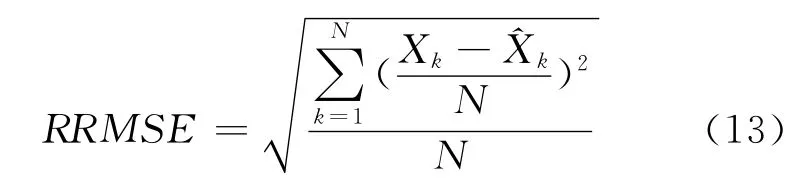
其中，Xk为序列的实际观察值，为Xk的预测值，N为原始流量数据序列预测元素的个数。

均方根误差和相对均方根误差的值越小，说明预测值与实际观察值越接近，预测效果越好。

为了进行横向比较，本节同时使用了小波分析与ARMA组合模型对该流量数据进行了预测，其结果如图3所示，预测效果量化指标如表3所示。图4截取了前30秒的预测结果。

Table 3 Comparison of forecasts precision表3 预测精度比较

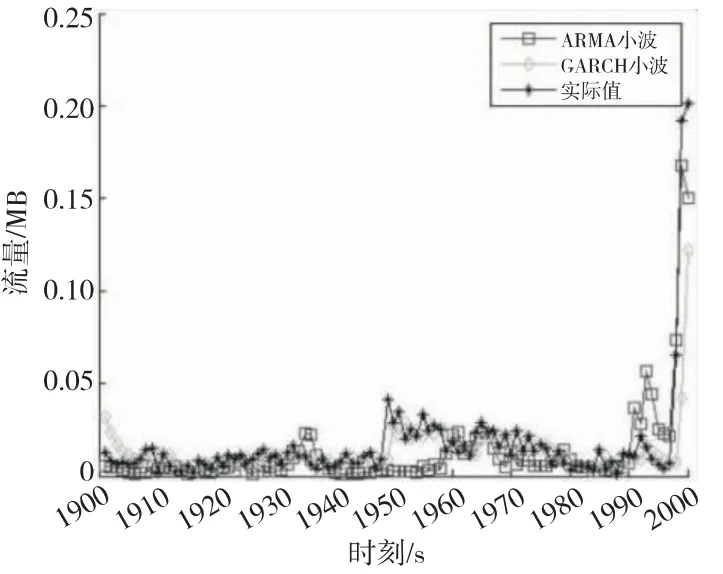
Figure 3 Comparison of the forecasts图3 预测结果对比图

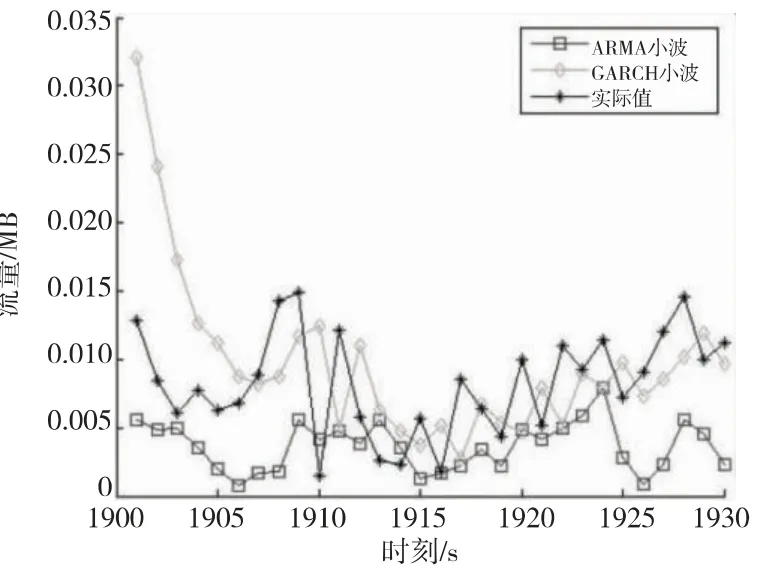
Figure 4 Details of comparison of the forecasts图4 预测结果放大对比图

4 结束语

本文对实际网络流量数据使用小波分析与GARCH组合模型进行了预测，仿真实验结果表明，小波分析与GARCH组合模型可以较好地描述网络流量数据的异方差性。由于实验数据具有“波动集群”现象，其方差是随着时间而变化的，这与传统的小波分析与ARMA组合模型的同方差假设不相符，因此小波分析与GARCH组合模型较之传统的小波分析与ARMA组合模型大幅提高了预测精度。而且，小波变换与GARCH模型的计算复杂度均为线性，因此该算法时间复杂度为O（N），在实际应用当中一般可行，在网络流量等非线性预测问题中应用前景广泛。

［1］ Jiang Ming，Wu Chun－ming，Zhang Min，et al.Research on the comparison of time series models for network traffic prediction［J］.Acta Electronica Sinica，2009，37（11）：2353－2357.（in Chinese）

［2］ Hong Fei，Wu Zhi－mei.Multiscale network traffic prediction model based on wavelet［J］.Chinese Journal of Computers，2006，29（1）：166－170.（in Chinese）

［3］ Dong Meng－li，Yang Geng，Cao Xiao－mei.Methods of network traffic prediction［J］.Computer Engineering，2011，37（16）：98－100.（in Chinese）

［4］ Wu wei，Liu Xi－yu，Yang Yi，et al.Analysis method of time array and two models of ARMA and GARCH［J］.Computer Technology and Development，2010，20（1）：247－249.（in Chinese）

［5］ Zhang Shan－wen，Lei Ying－jie，Feng You－qian.Application of time series with MATLAB［M］.Xi’an：Xidian University Press，2007.（in Chinese）

［6］ Cryer J D，Chan Kung－Sik.Time series analysis with applications in R［M］.Pan Hong－yu，translation.Beijing：China Machine Press，2011.（in Chinese）

［7］ Yi Dan－hui.Analysis of time series：Methods and application［M］.Beijing：China Renmin University Press，2011.（in Chinese）

［8］ Pan Hong－yu.Analysis of time series［M］.Beijing：University of International Business and Economics Press，2006.（in Chinese）

［9］ Wei Jin－wu，Wu Jiang－xing，Chen Shu－qiao.Joint multifractal model and characteristics analysis of network traffic［J］.Acta Electronica Sinica，2004，32（9）：1459－1463.（in Chinese）

附中文参考文献：

［1］ 姜明，吴春明，张旻，等.网络流量预测中的时间序列模型比较研究［J］.电子学报，2009，37（11）：2353－2357.

［2］ 洪飞，吴志美.基于小波的多尺度网络流量预测模型［J］.计算机学报，2006，29（1）：166－170.

［3］ 董梦丽，杨庚，曹晓梅.网络流量预测方法［J］.计算机工程，2011，37（16）：98－100.

［4］ 武伟，刘希玉，杨怡，等.时间序列分析方法及ARMA，GARCH两种常用模型［J］.计算机技术与发展，2010，20（1）：247－249.

［5］ 张善文，雷英杰，冯有前.MATLAB在时间序列中的应用［M］.西安：西安电子科技大学出版社，2007.

［6］ Cryer J D，Chan Kung－Sik.时间序列分析及应用：R语言［M］.潘红宇，等译.北京：机械工业出版社，2011.

［7］ 易丹辉.时间序列分析：方法与应用［M］.北京：中国人民大学出版社，2011.

［8］ 潘红宇.时间序列分析［M］.北京：对外经济贸易大学出版社，2006.

［9］ 魏进武，邬江兴，陈庶樵.网络流量的联合多重分形模型及特性分析［J］.电子学报，2004，32（9）：1459－1463.