基于无套利原理的资产证券化产品定价模型扩展
余粤
(中债信用增进投资股份有限公司,北京100033)
基于无套利原理的资产证券化产品定价模型扩展
余粤
(中债信用增进投资股份有限公司,北京100033)
基于高斯联结相依函数的单因子资产证券化定价模型由于其表达形式简洁、数值模拟简单,被业界广泛应用于资产证券化产品定价,但单因子模型对损失分布的刻画粗糙,无法充分估计尾部风险。使用基于损失分布特征函数的多因子模型对资产池的损失分布进行精细化的建模,在不增加参数要求的基础上提高了对损失分布构建的准确性。另外,对于目前我国市场上越来越多的单一标的资产证券化产品,也给出了具有解析解的定价方法。
资产证券化;无套利定价模型;损失分布;价值过程
一、引言
在当前国内经济增速回落的背景下,通过资产证券化的方式盘活流动性差的资产,可以增强经济的整体流动性,缓释存量信用风险。2013年7月国务院发布的《关于金融支持经济结构调整和转型升级指导意见》中要求逐步推进信贷资产证券化常规化发展;同年8月,国务院常务会议决定在严格控制风险的基础上扩大信贷资产证券化试点,均为我国资产证券化市场发展释放了积极的信号。事实上,2012年资产证券化重启后,中国人民银行、银监会、证监会、中国银行间市场交易商协会等部门主管的各类资产证券化产品累计发行额已超过1600亿元。
资产证券化产品作为复杂的信用衍生品,产品价格的准确计量,对发行方和投资者都有很重要的意义。赵亮等[1]基于一般信用衍生产品损失端和溢价端无套利原理,以2012年第一期开元信贷资产支持证券为例介绍了基于高斯联结相依函数(Gaussian Copula)的单因子模型[2]。虽然单因子模型表达形式和数值计算相对简洁,但由于模型在构建资产池损失分布时使用各资产平均违约率、平均相关性系数和平均违约损失率,因此模型存在一定局限性。首先,单因子模型中平均违约率的计算依赖加权平均评级因子(Weighted Average Rating Factor)的选择,而尽管目前我国评级机构在证券化产品评级报告中给出资产池的加权平均信用等级,但至今市场并没有一套公认的加权平均评级因子;其次,模型中平均相关性系数和平均违约损失率的选择缺乏系统性,事实上,同样基于单因子模型的Risk Metrics信用风险资本模型在不同平均相关性系数的假设下得到的VaR值差异巨大[3];再次,由于单因子模型基于高斯联结相依函数,模型无法准确描述资产池损失分布特征,也无法充分估计证券化产品的尾部风险,这使得高斯联结相依函数在美国次贷危机后饱受批评。除上述局限性外,单因子模型只适用于具有多个相关资产构成的资产池,而2012年资产证券化重启后,除了大量信贷资产池证券化产品(以中国人民银行和银监会主管ABS为主)外,还有越来越多的以单一企业资产或其收益权为标的的证券化产品(以证监会主管ABS和交易商协会ABN为主),对于这类产品,单因子模型也并不适用。
基于上述单因子模型的局限性,本文讨论使用多因子模型构建资产池损失分布的方法,同时针对单一标的资产证券化产品提出定价方法,并通过两种模型与单因子模型的比较,说明两种模型的优点和适用范围。
二、资产证券化无套利定价基础
本节简要介绍基于一般信用衍生产品损失端和溢价端无套利的定价原理。参考业界通行的定义方法,以整个资产池的百分比定义证券化产品分层,即假设产品共分M层,其中第x层的起始点为Ax-1(令最低层即次级层/权益层为第1层,起始点为A0=0,初始名义本金总额为AM=1),则第x层初始名义本金为Ax-Ax-1。
假设付息时点ti基础资产累计发生的违约金额比例为Z(ti),则ti时刻证券化第x层的损失比率为:
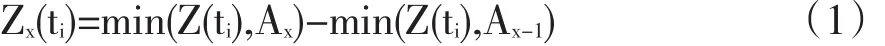
资产证券化产品的卖方需要对资产违约带来的预期损失支付收益率溢价。可以采用一般信用衍生产品定价的方法,分别求解各层损失端(Contingent Leg)和溢价端(Premium Leg)的现值,进而求得各层较无风险收益率的信用风险溢价。假定利率过程与各资产违约过程独立,并假设D(t0,t),t0≤t为t到t0的贴现因子,则对于资产证券化产品的第x层,分别定义其损失端和溢价端如下:
(1)损失端:资产证券化产品第x层的总预期损失在t0时刻的现值为:
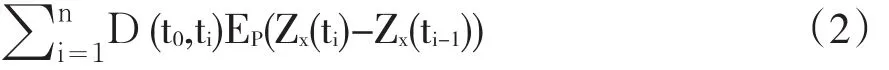
Zx(ti)-Zx(ti-1)为ti-1时刻到ti时刻第x层损失比率的增加值,对t0到tn各时段损失增加值的数学期望贴现到t0时刻,得到第x层的总预期损失在t0时刻的现值。
(2)溢价端:假设sx为第x层的风险溢价率,即利差,用于补偿第x层投资者因损失端信用风险产生的预期损失,则t0时刻第x层的溢价端现值为:
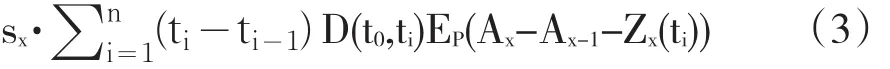
其中Ax-Ax-1-Zx(ti)为ti时刻第x层的剩余名义本金量,即为ti-1到ti时段内第x层的计息基数。将sx与各期时段长度、贴现因子和计息基数相乘并加总,得到t0时刻溢价端的现值。
根据无套利定价原理,令溢价端与损失端现值相等,即可求得第x层的利差sx为:
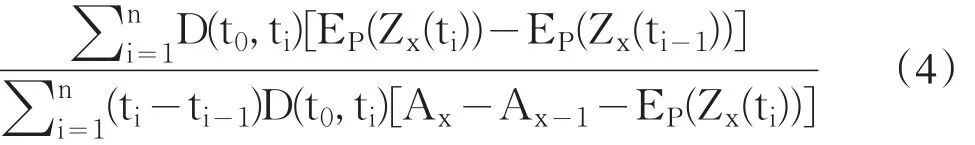
从上式可以看出,证券化产品定价的重点在于求解第x层损失比率Zx(ti)在测度P下的数学期望EP(Zx(ti))。本文的下面两章,就是在不同总损失Z(ti)假设下,讨论不同资产证券化产品的定价方法。
三、基于违约分布特征函数的资产池模型
考虑到本文引言所述单因子模型在构建资产池损失分布的局限性,本节放松单因子模型同质资产(违约率、损失率以及相关性一致)的假设,利用异构的单个资产损失分布构建资产池整体损失分布。
(一)多因子定价模型
参考前人研究成果[1],假定概率空间(Ω,F= (ℱt)0≤t≤T*,P),资产j(j=1,…,N)在t时刻的违约概率pj,t在一定假设下(如Merton模型[4]的假设)可表示为一ℱt可测正态随机变量ξj,t不大于非随机变量Kj,t的概率:
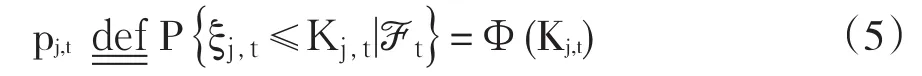
为了引入资产间的相关关系,假设正态违约因子ξj,t与正态公共因子Yt的相关性系数为ρj,t,即:
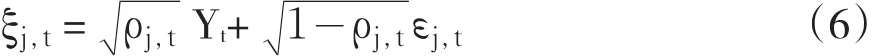
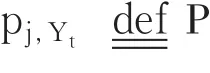
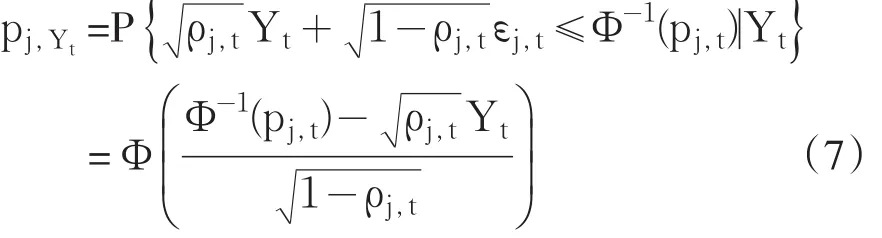
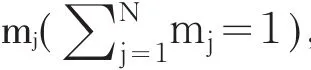
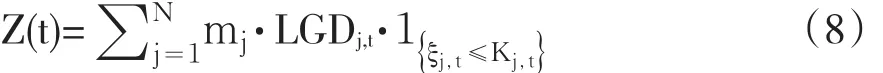
公式(8)是一系列随机变量的和,构建独立随机变量之和的分布函数一般采用各随机变量概率测度的卷积或通过下述特征函数方法间接求得:根据(8),Z(t)在给定公共因子Yt条件下的特征函数φZ(t)|Yt(u)为:
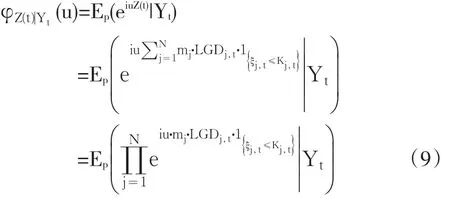
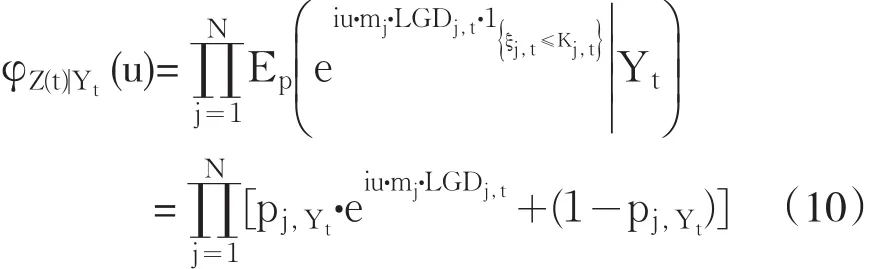
其中pj,Yt由公式(7)给出。由于Yt服从标准正态分布,积分可得到Z(t)的特征函数:
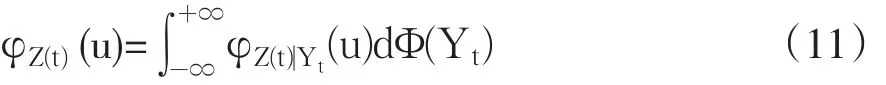
通过数值方法求得Z(t)的特征函数后,可通过傅立叶逆变换还原Z(t)的概率密度函数,进而求得第x层损失比率Zx(ti)在测度P下的期望EP(Zx(ti))。
(二)数值结果
上述资产池损失分布是通过构建N个伯努利随机变量(条件独立且非同分布)之和的特征函数,并通过傅立叶逆变换得到的,因此,为说明资产池损失分布的构建方法,不妨首先考察二项式分布(可以视为多个独立同分布伯努利随机变量之和)特征函数的傅立叶逆变换。图1比较了二项式分布特征函数离散傅立叶逆变换还原结果,左上图为其原始概率质量函数,右上、左下、右下三图分别为采样点为8、64、512个时离散傅立叶逆变换对特征函数的还原结果,可见,随着采样点个数的提高,还原结果逐渐逼近原始分布①由于傅立叶逆变换结果为连续函数,因此采样点数提高时,虽然变换结果的纵坐标值很高(例如右下图512个采样点时纵坐标值最高接近50),但曲线下的黎曼积分值将会收敛于原概率质量函数对应点的概率值。。
图1 二项式分布特征函数离散傅立叶变换还原结果
下面以2014年第一期农银信贷资产支持证券为例,比较使用单因子和多因子模型构建损失分布的结果,根据中债资信评估有限责任公司评级报告,证券化产品资产池行业和评级分布如表1所示②注意到目前我国信贷资产证券化产品募集说明书和评级报告中均只分别给出行业和评级这两个单一维度的资产分布状况,而并没有如表1所示的两维资产分布状况披露,因此表1为作者根据公开信息披露信息构造。本文选择2014年第一期农银信贷资产支持证券也是由于该产品所含贷款资产个数较少(仅为29个,其他产品大多在50个以上),便于由公开披露信息重构资产二维分布。:
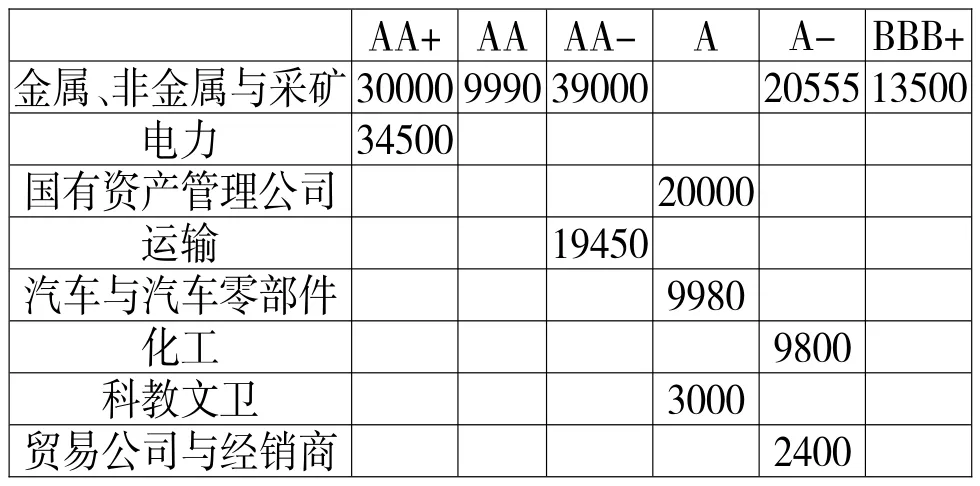
表1 农银信贷资产支持证券资产详情 单位:亿元
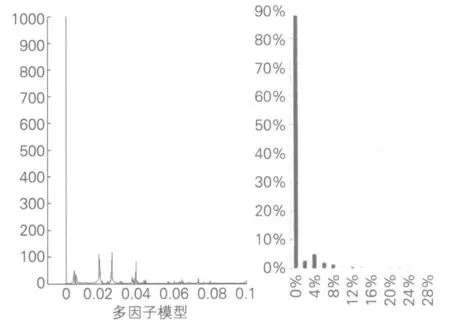
图2 多因子模型和蒙特卡洛模拟构建损失分布结果
参数选取上,使用各评级对应期限债券收益率曲线隐含的风险中性违约概率作为各资产违约率pj,t,各资产与公共因子相关性系数ρj,t采用深交所发布的行业指数与深成指之间的序列相关性③从公式(6)不难看出,且对于任意i≠j,违约因子ξi,t与ξj,t的相关性系数ρij,t为ρij,t = ρi,t∙ρj,t ,于是,若给出违约因子的两两相关系数矩阶[ρij,t]N×N,则资产j违约因子ξi,t与公共因子Yt的相关性系数ρj,t= =(i≠j≠k)。此处为简化处理,直接使用各行业指数序列和大盘指数序列的相关性。,不失一般性,假定各资产违约损失率均为40%。使用多因子模型构建资产池损失分布,如图2左侧所示。图2右侧直接截自中债资信《2014年第一期农银信贷资产支持证券信用评级报告》,报告中构建损失分布的方法为基于相关性矩阵Cholesky分解的蒙特卡洛模拟,从两图比较不难看出,多因子模型构建损失分布的结果同蒙特卡洛模拟结果相似,随着采样点个数的提高,结果逐渐逼近真实损失分布。
图3比较了使用单因子模型和多因子模型构建资产池损失分布的结果。可以看出,由于单因子模型参数只有平均违约率和平均相关性系数,因此模型对资产池损失分布的刻画非常粗糙,而通过多因子模型所构建的损失分布则充分揭示了损失分布的特性,并且对尾部风险给予了充分估计。
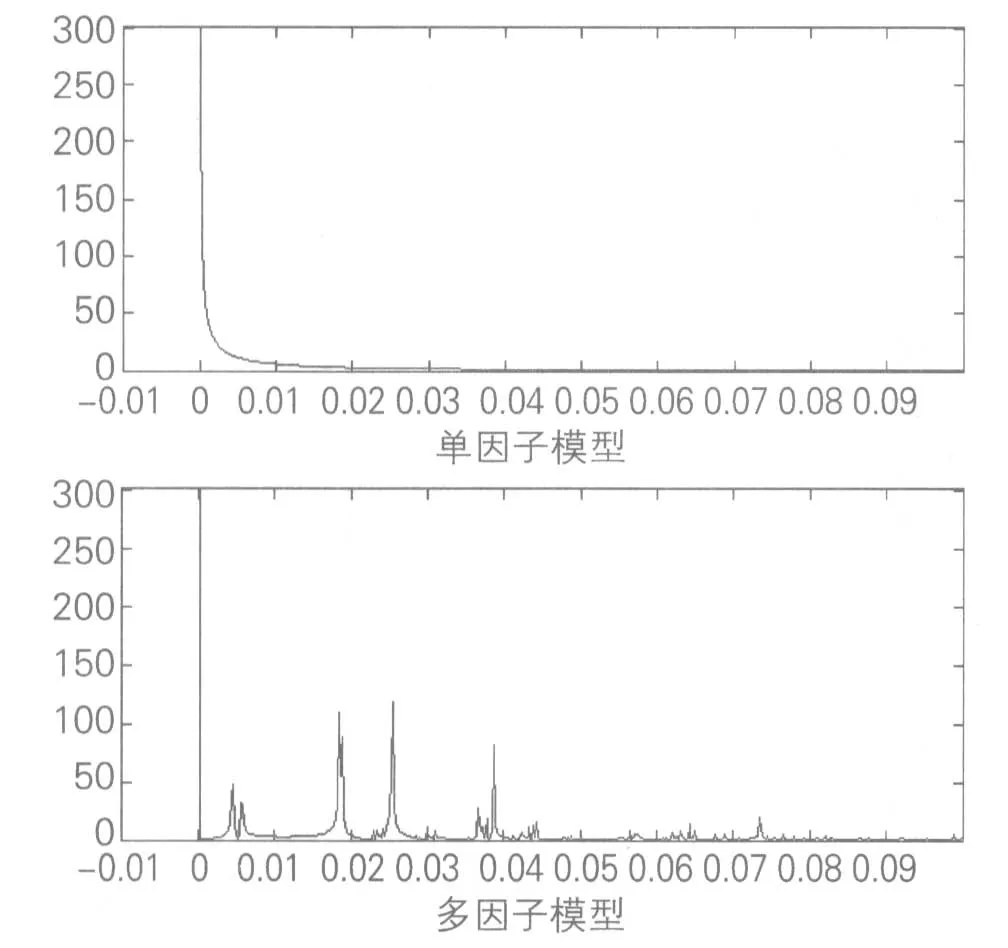
图3 单因子和多因子模型构建损失分布结果比较
实际上,通过表2中累积分布的比较不难看出,多因子模型较单因子模型体现出了明显的厚尾性。

表2 单因子模型和多因子模型累积损失分布比较
综上所述,多因子模型在没有大幅增加计算复杂度的基础上对于损失分布的构造明显优于单因子模型,对2014年第一期农银信贷资产支持证券资产池损失分布的构造结果与评级报告中蒙特卡洛模拟结果相符。基于损失分布进一步使用公式(4)即可对证券化产品第x层的溢价sx进行估值,这里不再赘述。
四、单一标的资产证券化产品定价模型
上述多因子模型与单因子模型均只适用于以多个资产构成资产池为标的的证券化产品,对应的大多是中国人民银行和银监会主管的信贷资产证券化产品,而目前由证监会主管的企业资产证券化和交易商协会主管的资产支持票据,标的大多为单一企业资产或其收益权。对于有稳定现金流的收益权类产品,可选用现金流支付瀑布(Payment Waterfall)模型,考虑证券在各离散付息时点资产和负债的现金流,进而对产品进行定价。然而,基于单一企业财务报表的现金流预测非常繁琐,且目前一些项目收益权的现金流本身并不足以覆盖产品本息,产品还款来源实际为企业或其产生收益权的基础资产的价值增值(例如以商业地产租金收入为标的的证券化产品还款实际来源为商业地产价值的增值)。基于上述考虑,本节介绍一种在证券化产品标的为单一企业资产或其收益权的情况下,利用标的资产价值变动对产品进行估值的方法。
(一)定价模型
假定概率空间(Ω,F=(ℱt)0≤t≤T*,P),并假定单一资产价值Vt在P下服从几何布朗运动:

初始条件V0=1。从第二节的讨论可知,对证券化产品定价的关键在于如何求得任一付息时点ti形如公式(1)的某一层损失比率Zx(ti)在测度P下的数学期望EP(Zx(ti)),而在单一资产假定下,任意时刻t整个证券化产品总损失比率为1-Vt,由公式(1)可知任意t时刻第x层的损失比率为:
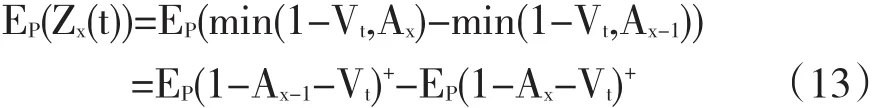
即EP(Zx(t))实际为两个执行价格分别为1-Ax-1和1-Ax的欧式看跌期权价值之差。
本文第二节所述证券化结构的定义和推导仅包含了对违约情况的处理,而从目前已发单一标的资产证券化项目来看,大多数具有提前偿付的机制,提前还款的现金流首先从最高优先级开始对本金进行偿付,较高优先层到期日较近,由于较优先的x层提前偿付,标的资产对证券化剩余的第x-1及以下层的覆盖程度更高,最终结果表现为剩余层利差的相对缩小,这里仅需将公式(13)中的1-Vt改为Am(t)-Vt即可:
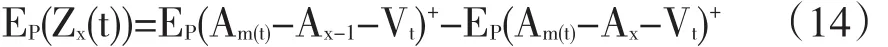
其中m(t)为截至t时刻尚未到期的最优先层的层数。
对两个期权分别使用Black-Scholes-Merton公式可得到EP(Zx(ti)),即:
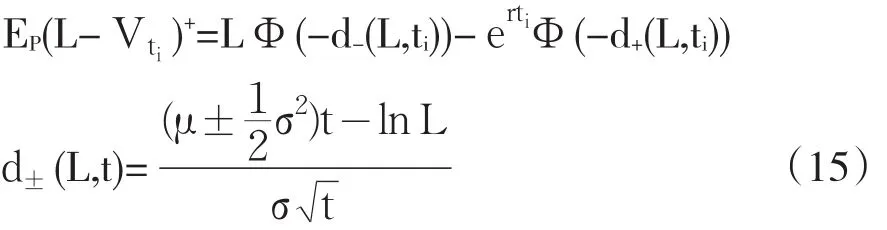
上式中L为Am(t)-Ax-1或Am(t)-Ax。综合公式(4)、(14)和(15),即可对单一资产证券化产品第x层的利差sx进行估值。
(二)数值结果
区别于单因子和多因子等资产池模型,本节所述单一标的资产证券化产品定价模型不再需要对标的违约率进行估计,而是在假设标的资产服从几何布朗运动的情况下,直接通过资产价值的变化估计各层损失,可以视为Merton结构化模型的一种扩展(Merton模型[4]可视为仅有净资产和负债两层)。因此,对单一标的资产证券化产品定价的主要参数包括:
(1)基础资产漂移μ,即资产价格的长期趋势;
(2)基础资产波动率σ;
(3)分层结构Ax-Ax-1(x=1,…,M);
(4)资产初始质押率,初始质押率决定了权益层A1-A0的大小,进而影响分层结构。
在下述算例中,假设证券化产品分为9层,其中权益层为20%,剩余优先层均为10%,假设提前还款从最优先级开始发生,每期偿还一层本金,即最优先层存续1期,次优先层存续2期,以此类推,同时假设基础资产价格的长期趋势为μ=5%,图4显示了各层风险溢价与资产波动率σ(0%—100%)的关系。
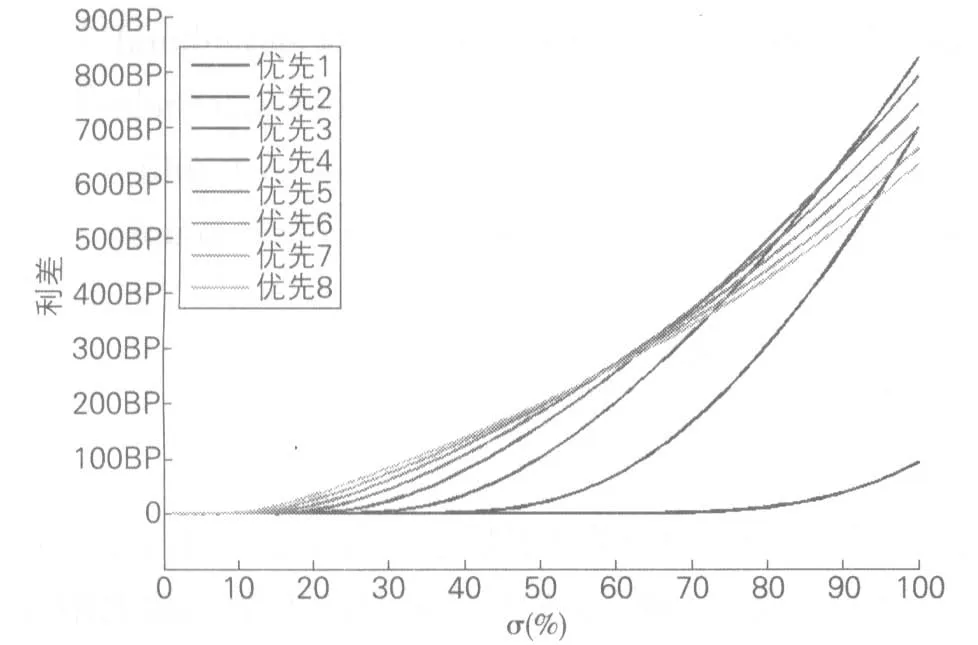
图4 证券化产品各层利差与资产波动率的关系
从图4中看出,在资产波动率正常范围内(≤30%),各优先层利差符合优先层顺序,即较高优先层的溢价较低,且各层与无风险利率的利差均在100BP以内,证明了市场单一标的资产证券化产品各优先层评级大多为AAA的合理性。在波动率较大情况下,各层利差出现倒挂,主要原因在于较优先层的提前偿付机制,即当较优先层提前偿付后,由于标的价值对剩余次优先层覆盖程度提高,导致次优先层风险降低,因而其利差相对较小。
本节给出的单一标的资产证券化产品定价模型虽基于基础资产价值服从几何布朗运动的假设,但由于把证券化产品每层的预期损失表示成了两个看跌期权之差,基础资产价值同样可以使用其他随机过程建模(如加入跳跃过程等[5]),因此适用于不同标的资产的情况。本节定价模型的结果与资产池证券化产品模型定价结果有相似之处,但由于方法具有解析解(单因子模型需使用数值积分、多因子模型需要使用离散傅里叶变换和数值积分等数值方法),因此便于对产品进行快速定价及参数敏感性等讨论。
五、结论与建议
资产证券化产品定价模型通常较为复杂,涉及参数较多,基于高斯联结相依函数的单因子模型由于使用平均违约率、平均相关性等简化参数,在业界得到了广泛的应用,但单因子模型也存在损失分布构建粗糙、尾部风险考虑不足、依赖加权平均评级因子、参数选取主观性较强等缺点。
对于单因子模型的上述不足,本文使用基于损失分布特征函数的多因子模型对资产池的损失分布进行更精细化的描述。考虑到单因子模型中平均违约率和平均相关性系数亦需要通过各资产违约率和相关性加权平均得到,因此多因子模型在不增加参数要求的基础上大大提高了损失分布构建的准确性。同时,通过对不同产品损失分布进行统计,多因子模型也可为构建适用于我国的加权平均评级因子提供方法和依据。
另外,对于目前我国市场上越来越多的基于单一企业资产或其收益权的资产证券化产品,本文也在同一无套利定价框架下给出了其定价方法。由于方法具有解析解,因此较损失分布模型和现金流瀑布模型更适于对产品进行快速定价及敏感性分析。
最后,模型估值只是资产证券化产品定价的第一步,只有在产品信息披露简单透明的基础上,才能引导投资人根据产品特点和自身数据积累选取合适的方法,从而促进产品流动性、控制产品风险。
[1]赵亮,余粤,孟琪.信贷资产证券化产品定价研究[J].金融理论与实践,2013,(3):41-46.
[2]O A Vasicek.Loan Portfolio Value[J].RISK, 2002,(12):160-162.
[3]O A Vasicek.Invited Talk:The Distribution of Loan Portfolio Value[C].Symposium on Credit Risk, National University of Singapore,2014.
[4]R C Merton.Theory of Rational Option Pricing [J].Bell Journal of Economics and Management Science,1973,(4):141-183.
[5]John Cox,Stephen Ross.The Valuation of Options for Alternative Stochastic Processes[J].Journal of Financial Economics,1976,(1-2):145-166.
(责任编辑:张艳峰)
1003-4625(2014)10-0073-05中图分类号:F830.91文献标志码:A
2014-08-12
本文为国家社会科学基金项目“量化宽松政策研究:理论、效应与中国选择”(编号:13BJL024)。
余粤(1983-),男,广东揭阳人,博士,中国社会科学院研究生院金融系博士研究生,中债信用增进投资股份有限公司高级经理,研究方向:货币理论与政策,金融衍生品,风险管理。

