基于F-MMC和LCC的混合型三极直流系统及其控制策略

许 烽，徐 政，刘高任，黄弘扬

（浙江大学 电气工程学院，浙江 杭州 310027）

0 引言

伴随着电力负荷需求的快速增长，现有的交流线路传输容量已难以满足发展要求。而土地资源的限制和时间、费用等问题也增加了新建一条线路走廊的困难和不可行性［1-3］。因此，需要选择其他有效的途径对现有交流线路进行扩容。传统扩容方法有多种，如采用紧凑型输电线路、提高导线的温度等级、装设 FACTS 设备等［1，4］。 但是，将交流线路改造成直流的方式更吸引人［5-7］，这种方式不仅具有更大的扩容潜力，而且还具有快速控制和网络分割能力，能够缓解交流系统存在的一些问题，如短路电流越限、低频振荡加剧、故障大范围传递等。

文献［8］提出了一种三极直流结构，利用特殊的电流调制策略，能够更大程度地提高线路改造后的输电容量，其中，极1和极2采用晶闸管换流器，极3采用由反并联晶闸管组成的换流器或反向并联的换流阀组成的换流器［8-11］。基本换相单元为晶闸管，与传统直流输电系统类似，存在换相失败、过电压等问题［12-14］，同时在过渡过程中，由于直流电压和直流电流需要大范围变化，还存在如下缺陷：

a.直流电流变化伴随有无功变化，由于无功设备调节缓慢，因而会引起交流系统无功剩余或不足，产生电压波动；

b.极3在电流调制过渡阶段，其直流电流需要反向，存在过零点现象，而传统直流具有最小直流功率（电流）的要求［15-16］，一般为额定值的 10%左右，因而，过渡阶段容易引发过电压等问题；

c.每个过渡阶段，极3都需要进行闭锁和解锁动作，如果没有严格的操作时序保证，容易引起过电压和过电流。

全桥子模块 FBSM（Full Bridge Sub-Module）具有输出+1、0、-1这3种电平的能力，且电流能够双向流通，因此，基于全桥子模块的模块化多电平换流器（F-MMC）具有直流电压和直流电流双向运行能力。三极直流的极3需要每间隔一定的周期时间进行一次直流电压和直流电流的反向变化，必然需要采用具有直流电压和直流电流双向运行能力的换流器，而F-MMC正是选择之一。将F-MMC用于极3，则交流侧形成了电网换相换流器 LCC（Line Commutated Converter）和F-MMC并联的结构。根据文献［17］的表述，电压源换流器 VSC（Voltage Source Converter）类换流器能优化LCC的稳态和暂态特性，因此，通过引入F-MMC，能够较好地缓解和避免现有三极直流系统的缺陷，提升整个三极直流系统的运行特性。

本文根据所提出的混合型三极直流系统，针对转换过渡阶段遇到的无功（电压）平衡、电流平衡和电容电压平衡3个主要问题，提出相应的控制策略，并利用PSCAD/EMTDC进行了仿真验证。

1 系统结构及电流调制策略

1.1 系统结构

图1（a）是混合型三极直流系统结构示意图，其由双极直流和单极直流并联组成。与常规的双极直流结构不同的是，极1和极2之间的中性点电流不流入大地，而是通过具有双向流通能力的极3进行回流。其中，极3采用F-MMC，如图1（b）所示；极 1和极2的换流站都采用12脉动晶闸管换流器，如图1（c）所示，属于LCC。LCC和F-MMC都具有直流故障自清理能力，因此，混合型三极直流结构适用于架空线输电。通过在换流器出口处装设平波电抗器，能够平抑直流纹波，同时防止雷电等冲击波进入换流站导致器件遭受过电压而损坏。

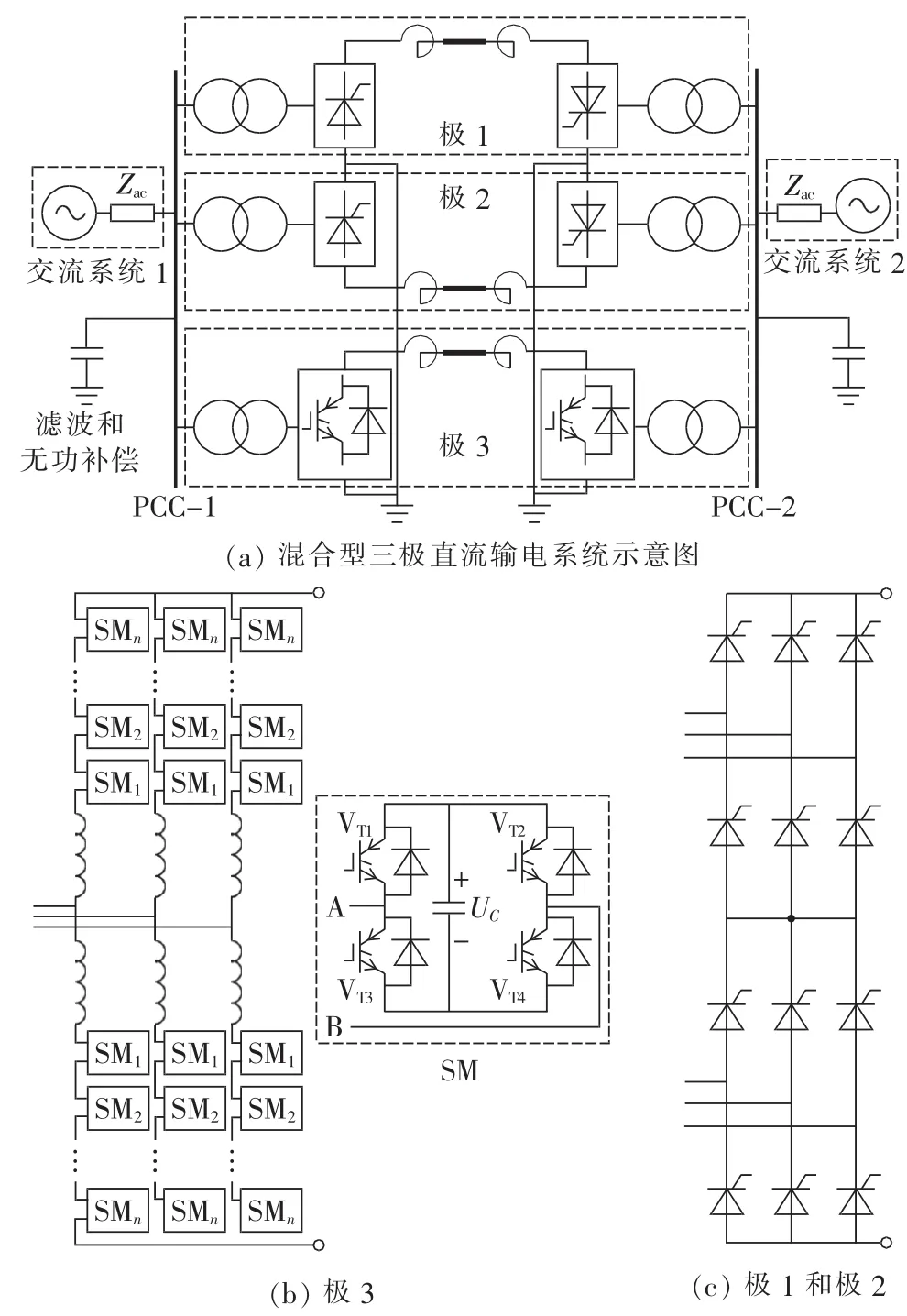
图1 混合型三极直流输电系统示意图Fig.1 Schematic diagram of hybrid tripole HVDC system

1.2 电流调制策略及其影响

文献［8-11］对三极直流系统的电流调制方法进行了具体阐述，电压电流调制过程如图2所示。其指出，当电流调制比为3.73时，可以获得最大传输功率，为双极直流的1.37倍。从图2可以看出，每个过渡阶段包含2个电流调节过程和1个电压反向过程。通过电流调节和电压反向的错时处理，可以尽可能地减少整个过渡阶段的有功功率波动，有利于交流系统稳定运行。

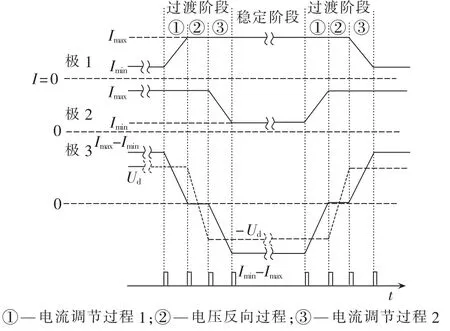
图2 电流调制时序图Fig.2 Sequence chart of current modulation

在2个电流调节过程中，极1和极2的LCC轮流进行直流电流的调节变化，极3根据极1和极2的电流差进行补偿调节，使得此过程满足交直流系统间的有功功率平衡。但是，LCC不具有无功调节能力，在电流变化过程中，会引发无功变动，引起公共连接点 PCC（Point of Common Coupling）电压波动。因此，需要通过F-MMC的无功调节能力来就地平衡此部分变化的无功，维持PCC电压稳定。在电压反向过程中，LCC不作任何变化，F-MMC进行极3直流电压反压控制。整个过程要求极3的直流电流始终维持为0，以免引发接地电流和有功功率波动，同时，要求F-MMC子模块的电容电压保持平衡，防止发生过电压或欠电压，影响整个系统的运行。因此，根据上述分析，混合型三极直流系统的整个过渡过程需要着重注意以下3点：①无功（电压）平衡；②电流平衡；③FBSM电容电压平衡。

为更加清楚地描述上述问题①和②，采用如图3所示的三极直流单侧等效模型进行说明。其中，Ue和δ1、Us和δ2分别是交流等效电源和PCC的电压幅值和相角；Le是交流系统等效阻抗；Ps和Qs分别是交流系统的有功和无功功率；Qh是滤波器和无功补偿器输出的无功功率；Pi、Qi、Udi和 Idi（i=1，2，3）分别是每极吸收的有功功率、吸收的无功功率、直流电压和直流电流。

图3 三极直流单侧等效模型Fig.3 Unilateral equivalent model of tripole HVDC

对于无功（电压）平衡而言，其目的在于控制PCC电压Us保持稳定不变，利用潮流计算，可以得到如下表达式：

通过消去 δ2，得到：

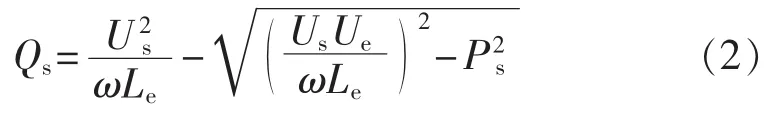
对于具体系统而言，Ue、δ1、ω、Le均确定，且图 2所示的调制策略可确保过渡阶段Ps基本保持不变。因此，从式（2）可以看出，Qs和Us直接关联，维持Us不变可通过维持Qs不变实现。假设控制能够维持Us不变，则对于PCC而言，存在如下无功方程：

由于Us保持不变，则Qh和Qs也维持不变，进而Q0不变。F-MMC无功平衡控制的目标便是控制3个极吸收的总无功功率保持不变，即始终满足Q1+Q2+Q3=Q0。

对于电流平衡而言，3个极直流电流的关系需始终满足式（5），尤其是过渡阶段，若不满足，不平衡电流将流过接地点，三极直流传输的有功功率将不能保持恒定。

2 LCC控制策略

从图2可以看出，极1和极2换流站内的LCC在过渡阶段需要控制直流电流，同时为了保证有功平衡，在电流调节过程中，应尽量保持3个极的直流电压相等，因此，极1和极2的LCC需要分别控制直流电压和直流电流。本文LCC的控制策略参照国际大电网会议（CIGRE）直流输电标准测试系统控制器的结构和参数［12］。

2.1 整流站

整流站直接沿用CIGRE的控制器，即采用定电流控制和最小触发角控制。

2.2 逆变站

逆变站的控制结构如图4所示。其中，Udmes、Idmes和γmes分别为直流电压、直流电流和关断角的测量值；Udref、Idref和 γmin分别为直流电压、直流电流的参考值和关断角最小值；Imarg为电流裕额，一般取Idref的10%。

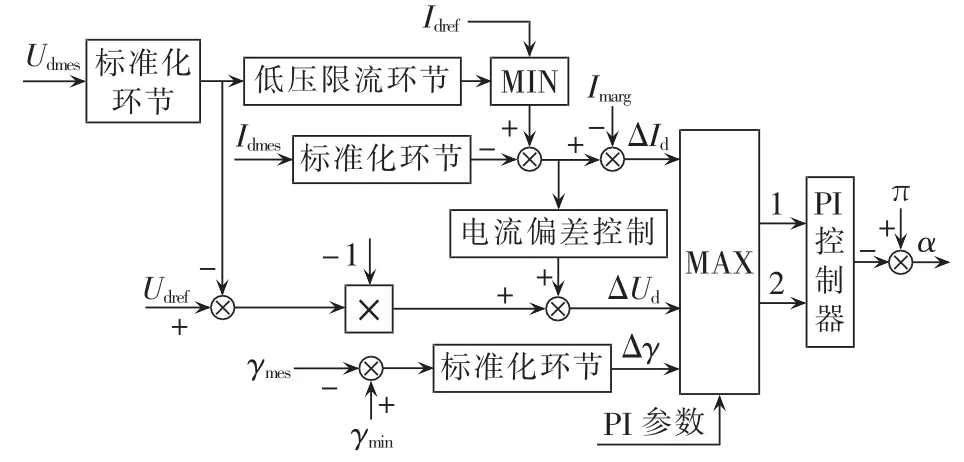
图4 逆变站控制框图Fig.4 Block diagram of inverter station control

上述控制器与CIGRE的控制器的不同点在于：在定电流控制和定关断角控制基础上引入了定电压控制，非暂态情况下，定电压控制作为主控制；控制方式的比较选择信号直接采用信号的偏差量，而不是经过 PI环节后的信号。 各偏差量（ΔId、ΔUd、Δγ）经过最大值比较后，1号端输出选中方式下的信号偏差量，2号端输出相应的PI参数，再分别输入PI控制器。由于直流电压、直流电流和关断角单位量纲和额定数值差异大，不具备直接比较条件，所以设置了标准化处理环节，将比较量归算至某统一量，进而使得各控制方式下的偏差量具有可比性。

3 F-MMC控制策略

F-MMC的等效数学模型与MMC相同，上下桥臂的参考电压可表示如下［18］：

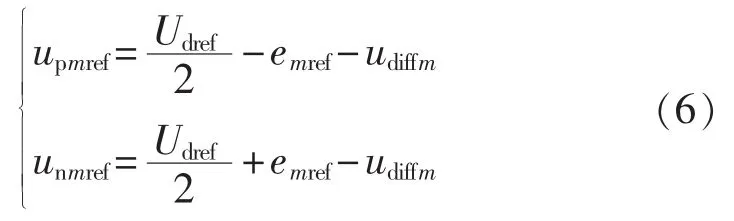
其中，Udref为直流电压参考值；emref（m=a，b，c）为 m 相内部电势参考值；udiffm为m相内部不平衡电压。

F-MMC的整体控制结构如图5所示，采用内外环控制方式。整流站的外环采用改进直流电流控制MCC（Modified direct Current Control）以及交流电压控制 AVC（Alternating Voltage Control）用于控制直流电流和交流电压，逆变站采用直流电压控制DVC（Direct Voltage Control）和AVC用于控制直流电压和交流电压。

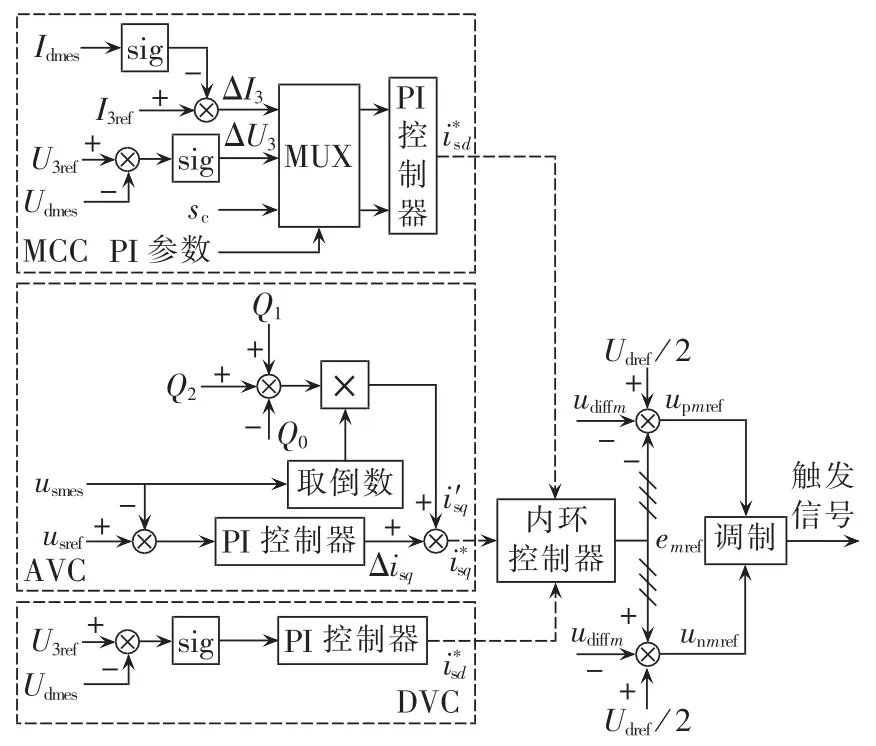
图5 F-MMC控制框图Fig.5 Block diagram of F-MMC control

3.1 MCC

MCC由直流电流控制和直流电压控制两部分构成，主要目的在于控制极3的直流电流在电压反向过程中保持为0。其中，U3ref和I3ref分别为极3直流电压和电流的参考值；Udmes和Idmes分别为直流电压和电流测量值；sc是控制方式选择信号，当系统处于非电压反向过程时，选择器MUX输出电流控制偏差ΔI3并选择相应的PI参数，反之输出ΔU3及相应PI参数；sig为极3直流电压正负标志信号，表达如式（7）所示。

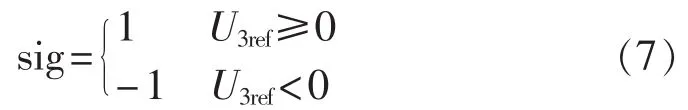
如果极3整流站在电压反向过程中仍采用电流控制方式。当直流电压参考值开始朝着反向变化时，逆变站的直流电压能够通过DVC跟踪参考值，随之变化，但是整流站的直流电压不会与逆变站同步变化，原因在于电流控制只有在电流出现偏差的情况下才起作用，当整流站和逆变站因电压偏差导致电流偏差时，整流站的电流控制器才开始起作用，令整流站的直流电压发生变化，以维持原直流电流，因而，其直流电压变化必然慢于DVC的逆变站。上述控制过程在直流电压反向过程中将一直持续发生，整流站和逆变站的电压偏差始终存在而难以消除，进而使得极3的直流电流一直存在波动而不能维持为0。这一方面会引起直流功率波动，影响交流系统的特性；另一方面，极3波动的电流将馈入接地点，对交流系统和地下金属设备产生不利影响。

在电压反向过程中，如果MCC的直流电压控制起作用，由于整流站和逆变站都处于直流电压控制状态，两者对于直流电压的响应特性将较为接近，从而达到间接控制极3的直流电流维持为0的效果。为达到较好的控制效果，MCC中直流电压控制相对应的PI参数选择也较为简单，直接采用逆变站DVC的相同或相近PI参数即可。

3.2 AVC

根据1.2节的阐述，在过渡阶段，为维持交流系统无功和电压稳定，控制交流电压和控制无功功率具有相同的效果。对于F-MMC而言，控制交流电压显得更加直观简洁，因而，本文在无功控制方面采用交流电压控制。

在电流调节过程中，LCC吸收的无功功率会发生变化，根据式（3）可知，要使得交流电压保持不变，F-MMC的无功也要作相应变化。本文引入稳态逆模型，利用前馈附加控制来减少调节过程中交流电压的波动幅度。在标幺制下，取电网电压矢量的方向为d轴方向，极3无功表达式如下：

其中，usd为PCC交流电压d轴分量；isq为PCC流入F-MMC电流的q轴分量。结合式（3），可得前馈输出的无功电流为：

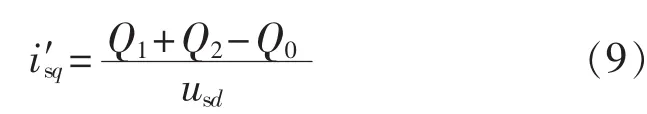
为加速控制器的响应速度，Qi（i=1，2）通过如下表达式计算得到：

其中，Udi、Idi、αi和 μi分别为直流电压、直流电流、触发角和换相角，当计算逆变站吸收的无功功率时，只需将触发角αi换为关断角γi。

图5中AVC的PI控制器主要为消除静态误差，输出Δisq与逆模型输出的预算值相加作为无功电流的参考量，采用稳态逆模型和PI控制器相结合，能够提高控制器的响应速度并消除静态误差。

3.3 调制策略及F-MMC运行模式

3.3.1 调制策略和电容电压平衡

F-MMC含有较多的子模块数，尤其是在高电压大容量情况下，为降低损耗，一般采用低频开关调制策略。根据目前研究成果，有3种常用的低频开关调制方法：特定谐波消去法SHE（Selective Harmonic Elimination）、空间矢量控制 SVC（Space Vector Control）和最近电平控制 NLC（Nearest Level Control）。正如文献［19］所分析，本文采用简单有效且适用于子模块较多情况下的NLC。

图6给出了NLC框图。将桥臂参考电压upmref或unmref除以单个子模块电容电压UC，然后通过最近取整函数round（·），得到最终投入的桥臂电平数S（定义单个子模块输出电压为+UC的称为一个正电平，单个子模块输出电压为-UC的称为一个负电平），S可正可负，由F-MMC的运行工况决定。

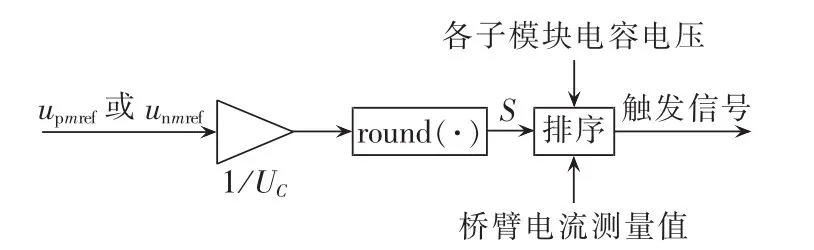
图6 最近电平控制原理图Fig.6 Schematic diagram of NLC

直流电压反向过程中，要求直流电压按照固定的变化率实现反向，但同时子模块电容电压保持稳定。电容电压偏高会降低设备的绝缘特性，而偏低将有可能使得交流电压和直流电压的控制不能得到实现。从直流电压角度来看，极3的直流电压由下式确定：

其中，Spm和 Snm分别为 m（m=a，b，c）相上桥臂和下桥臂的电平数。为达到直流电压Ud3反向、电容电压UC保持稳定的要求，只能通过改变Spm+Snm实现。根据式（6），并利用环流抑制措施［20-21］，可获得如下表达式：

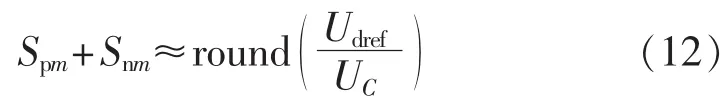
从上式可以看出，Spm+Snm与直流电压参考值Udref成正相关，当直流电压因反压需要改变其参考值Udref时，相单元电平数Spm+Snm也会随之改变，因而满足式（11），维持电容电压稳定。

从上述分析可以看出，在式（6）和图6控制下，F-MMC能顺利实现直流电压反向功能，同时维持电容电压稳定。

3.3.2 F-MMC运行模式

FBSM 能输出 3 种电平：+UC（+1）、0 和 -UC（-1）［22］。假设桥臂的子模块数为N，桥臂中第i个子模块电平为ui。设定ui=+1的子模块个数为J，ui=-1的子模块个数为K，则ui=0的子模块个数为N-J-K。图6得到的桥臂电平数S可以表示成如下形式：

正电平数J、负电平数K以及零电平数存在如下约束：

假设 N 为偶数，根据式（13）和（14），可以得到：

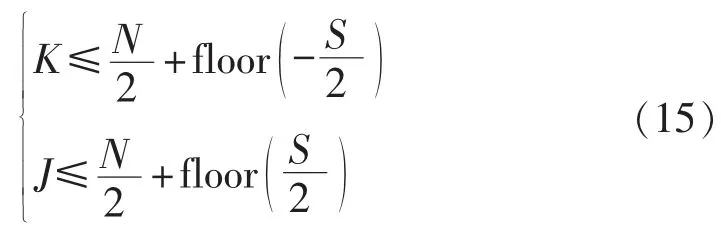
其中，函数 floor（·）为去尾取整函数。 根据式（13），J与K成正比例关系，当J取得最大值时，K也为最大值，反之亦然。因而，根据S值的正负性，可以得到如下表达式：

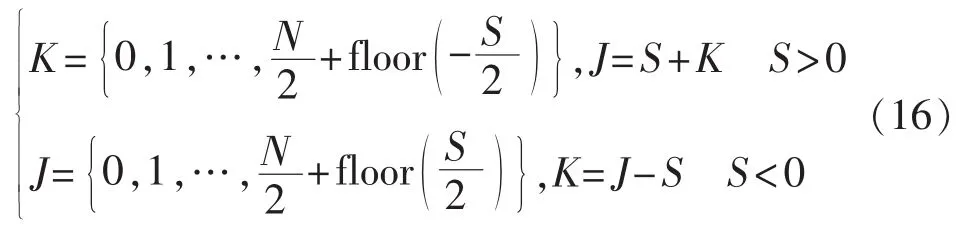
当S＞0时，J的取值由K决定；当S＜0时，K的取值由J决定。在S确定的情况下，由式（16）可以看出，（K，J）的组合选择有多种，即F-MMC有多种运行模式。其中最常见的2种模式为：当S＞0（S＜0）情况下，如果 K（J）设置为最小值 0，那么 J（K）也将取得最小值，此时零电平数将取得最大，因此，此模式可以称为最大零电平模式；如果K（J）设置为最大值，那么零电平数将取得最小，称为最小零电平模式。最小零电平数可能取0，也可能取1，与S的奇偶性相关。

运行模式的选择和F-MMC的损耗密切相关，文献［23］指出损耗的分布与系统运行工况有关。因而，分析F-MMC的损耗与运行模式之间的问题需要进行分类讨论。本文在此不作展开讨论，而直接采用最大零电平模式。

4 仿真分析

为了验证所提出的混合型三极直流的可行性以及控制策略的有效性，在电磁暂态时域仿真软件PSCAD/EMTDC内搭建了一个如图1所示的详细仿真模型。

4.1 系统参数

针对图1所示的三极直流系统，额定功率为2000 MW，其中，每一极的额定直流电压均为500 kV，极1和极2轮换的直流电流Imax和Imin分别为2 kA和1 kA，极3的额定直流电流为1 kA，因而LCC总的额定功率为1500 MW。整流侧和逆变侧交流系统参数相同：电动势 525 kV，Zac=34.7∠80°Ω，短路比SCR为5；F-MMC每个桥臂含有250个子模块，子模块电容为7500 μF，电容额定电压2 kV，桥臂电感为37.2 mH。功率从交流系统1（送端）送向交流系统 2（受端）。

4.2 仿真分析

图7和图8给出了整流站系统稳态运行的仿真波形，其中，电压基准为500 kV，电流基准为1 kA，功率基准为500 MW。根据要求，一般需要过渡阶段的时间为4 s以上，正常阶段的时间为4～5 min。为观察方便，仿真部分作了必要的改动，在t=2.0 s时刻，系统状态已经稳定，2.0～4.8 s为第一过渡阶段，4.8～7 s为正常阶段，7～9.8 s为第二过渡阶段。

图7（a）为极 1（P1）、极 2（P2）和极 3（P3）的直流电压（标幺值），极1和极2的直流电压基本保持不变，极3的直流电压在过渡阶段实现反向。图7（b）为3个极的直流电流（标幺值），极1和极2的直流电流在过渡阶段进行轮换，而极3的直流电流实现了反向，以维持功率传输的一致性。图7（c）和图7（d）分别是极1、极2的触发角和关断角，伴随着直流电流的改变，极1和极2的触发控制角也依次发生轮换。

为验证本文提出的MCC控制器的有效性，及反压过程中电容电压的稳定性，图8给出了电压反向过程的仿真波形。图8（a）为接地电流（标幺值），可以看出，接地电流的波动很小（-0.03～0.02 p.u.）。图8（b）为整流站和逆变站F-MMC控制器输出的有功电流（标幺值），两者的响应特性非常接近，说明MCC能够使得整流站的控制特性较好地跟随逆变站，保证两侧直流电压相近，进而较好地维持极3的直流电流为0。图8（c）为子模块电容电压，反压期间，电容电压能够较好地维持在2 kV左右。

图7 内部特性仿真波形图Fig.7 Simulative waveforms of internal performance

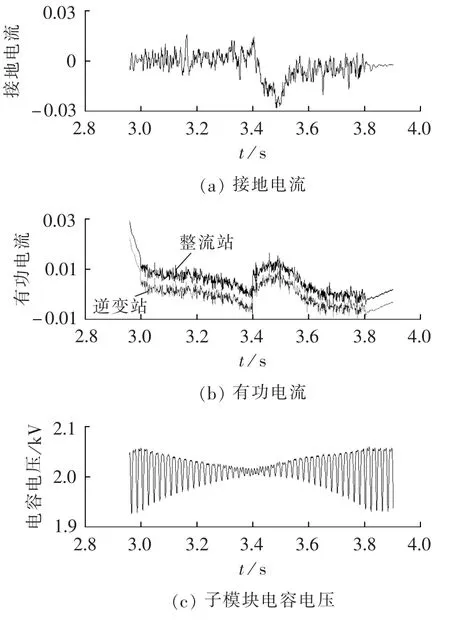
图8 接地电流和电容电压仿真波形图Fig.8 Simulative waveforms of grounding current and capacitor voltage

图9（a）为交流系统与PCC之间传输的有功功率（标幺值），在过渡阶段，有功功率会发生波动，波动范围为 4.05～4.17 p.u.，扰动量占稳定功率（4.12 p.u.）的2.91%，在可接受范围内。图9（b）和（c）分别为交流系统与PCC之间传输的无功功率（标幺值），以及PCC的交流电压有效值（基准为525 kV）。稳定阶段，交流系统与PCC之间交换的无功功率为-0.11 p.u.，在过渡阶段，无功波动为-0.13～-0.08 p.u.，波动较小。PCC的交流电压有效值波动范围为0.959 5～0.961 p.u.，占交流稳定电压的0.16%，波动极小，也间接证明了过渡阶段无功功率波动很小，表明所提出的AVC控制器能够很好地实现无功就地平衡，维持PCC的电压稳定。图9（d）和（e）分别为3个极吸收的有功功率（标幺值）和无功功率（标幺值），可以看出，无功功率的变动和有功功率成正相关，功率变化平滑、无突变，有利于交直流系统稳定运行。

图9 外部特性仿真波形图Fig.9 Simulative waveforms of external performance

5 结论

本文结合LCC和F-MMC提出了一种混合型三极直流系统。针对过渡阶段无功平衡、电流平衡和子模块电容电压平衡问题，利用F-MMC的特性优化能力，提出了相应的控制策略。仿真结果表明：系统无论是处在稳定阶段还是过渡阶段，都能保持稳定运行，系统各运行状态不会发生突变；过渡阶段，PCC交流电压基本保持不变，交流系统和PCC之间交换的功率，其波动幅度在可接受范围内；电压反向过程中，接地电流基本维持为0，从而保证了3个极之间的电流（功率）平衡，同时，子模块电容电压的平均值基本维持不变，不会出现过电压或欠电压等问题。