用列表格法分析数量关系解决数学应用题

张以德

从小学到初中，大多数学生遇到文字比较长的应用题一直不知道怎样去分析，去寻找题中的数量关系，不知道怎样把实际问题化成一个数学问题，建立数学模型。从上学期开始，我尝试采取用表格分析的方法，帮助学生解决列方程解应用题。先列表格，把求解目标、已知条件分列出来，使数量关系明朗化，列方程就容易了。

列表法就是借助于列出表格的形式进行解题的一种方法，在有些应用题里，各种数量间的关系比较隐蔽，一下子不容易看出，而且条件繁多，变化复杂，遇到这些题目时，可以采用列表法来分析条件。列表时，可以先根据题意画出表格，然后把问题中所有的已知量、未知量、隐蔽条件和所求量，用通用的记号、符号、字母等来代替，逐一填入表格中。而把问题中无关要紧的语句去掉，使我们能集中注意力考虑问题，迅速地找到等量关系，从而使问题得到正确解决。下面举几个例子加以说明。

例1：广东宏远队的朱芳雨是中国男篮的主力前锋，在一场洲际杯比赛中，他一人独得23分（不含罚球得分）.已知他投进3分球比2分球少4个，他一共投进了几个3分球和几个2分球？

认真阅读上述题目，我们思考以下问题：

1.题中涉及哪几个量？

2.投中3分球个数和2分球的个数关系如何？得分是多少？

3.题目中的相等关系是什么？（3分球得分+2分球得分=23；2分球个数-3分球个数=4）.

假设投中3分球个数为x个，填写以下表格，根据表格和相等关系列出方程求解，并想一想你能列出其他方式的表格吗？

到了七年级，学习了二元一次方程组，本题可以假设两个未知数，利用以上两个等量关系，列出两个方程，构成方程组求解，更易于理解。

如此，我在问题情景中，初步体验用表格分析问题各量间的相互关系，感受到列表格是解决问题的一个重要手段.

例2：某商店以2400元购进某种盒装茶叶，1月份每盒按进价增加20%作为售价，售出50盒。2月份每盒以低于进价5元作为售价，售完余下的茶叶。在整个买卖过程中盈利350元。求每盒茶叶的进价。

第一步，静心读题理头绪

题意叙述了购进茶叶以及分两个月售完茶叶的过程；题目中有三类不同实际意义的数量：单价，茶叶的盒数，总价；理清这两方面的头绪后，就用表格框架表示出来。

第二步，分析数量填表格

先设购进茶叶的单价为每盒元x，再在表内填入已知数量：购进茶叶的总价2400元，1月份售出茶叶50盒。然后用的x代数式分别表示，1、2月份售出茶叶的单价，表示购进茶叶的盒数和二月份售出茶叶的盒数。在这基础上，以单价与盒数相乘，分别表示1、2月份售出茶叶的总价，得到如下表格（见下表）：

第三步，两个方面作比较

题目还有个条件：盈利350元。就是把两个月售出的总价之和与购进的总价比较，售出的总价之和多350元。

第四步，平衡多少列方程

从“多=少+差”的角度平衡这两方面，列出方程：

50（1+20%）x+（x-5）（2400/x-50）=2400+350

（下略，答案是：每盒茶叶的进价是40元）

用列表法分析条件，不但眉目清楚，而且条件也不会遗漏，对初学者来说，是比较实用的。下面再举一例。

例3：七年级学生去距学校10千米的博物馆参观，一部分同学骑自行车先走，过了20分钟，其余同学乘汽车出发，结果他们同时到达。已知汽车的速度是骑车同学速度的2倍，求骑车同学的速度。

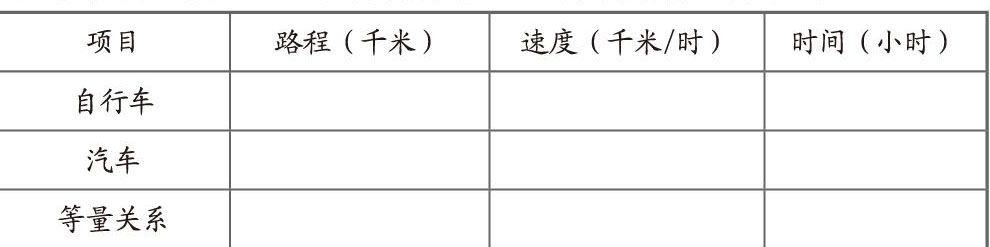
思考：这是匀速运动问题，它涉及到三个量：路程，速度，时间，其关系式为S=Vt，现分自行车、汽车两种情况列表如下：

在中学数学应用题中，这类问题一般编有两层或两方面的内容（如本题中的自行车和汽车），而在三个关系量中，每方面只具体地给出一个已知量（如本题的距离10千米），其他两个量不明确给出（如本题两种车的速度和这两种车到达博物馆所用的时间），题中还给出了三个量之间的等量关系（如题中有：⑴自行车比汽车多用20分钟。⑵汽车的速度是自行车速度的2倍）。

现把已知条件填入上表，进行观察：

？

由上表可以看出，本题共有4个未知量，若想列一元方程来解，就假设一个未知数x来表示这4个未知量中的任何一个，这样一来就有4种设法，到底采用哪一种设法较好呢？一般地说：（1）题目要求什么，就设什么为x；（2）列未知数的系数为整数优于分数。

根据公式S=Vt（隐含着的等量关系）和上面所说的设元方法，现设自行车的速度为x千米/时，填得如下表：

其中，2x利用了题设中的等量关系：汽速=自行车速度的2倍，利用了隐含的等量关系；

没有利用的等量关系是：自走时间-汽走时间=20分钟 ，据此，可列方程：_______-_______=________，求得自行画的速度为每小时15千米。

换个角度思考，如果把本题的要求改为：骑车同学到博物馆用了多少时间？则可设汽车到达博物馆用了x小时，也可以得到下表：

对于任何一个应用题，只要仔细地分析题中的数量关系，都可以得到几个不同的方程方程的意义，这正是我们建起方程的根本。用表格法分析题中的数量关系与线段、图解法一样，仅仅是分析的一种手段而已，并没有什么独创之处。能用表格法分析的应用题，同样也可以借助于其它工具分析。但对于有几个量限制的问题，通过表格法我们更容易理清各个量之间的关系，降低题目难度，快速找到等量关系，列出方程。

几点说明：

1.针对不同的应用题，可以设计不同的表格。表格的横向反映不同数量的关系，即：每份数×份数=总数；表格的纵向反映题目包含的不同阶段或不同方面。

2.填表后总有一个条件没有用过，正好用来列方程。

3.在用此法解决问题时，随着解题的着眼点的不同，表格的形式也不是千篇一律的，必须在实践中灵活运用。