板式加劲梁悬索桥锚跨索股分析

田仲初，崔后吉，彭文平，周 旭

(长沙理工大学土木与建筑学院，湖南长沙 410114)

1999年至今，中铁大桥勘测设计院共设计了6座板式加劲梁悬索桥［1］:其中在贵州省的5座分别是落脚河大桥、西溪大桥、北盘江大桥、阿志河大桥以及在建中的息烽至金沙公路乌江大桥，均采用的是预应力混凝土板式加劲梁。广西柳州市的红光大桥为钢板式加劲梁。结合桥址区的地形特点，主桥均采用单跨双铰式悬索桥布置，主缆采用预制平行钢丝索股。由于主缆直径较小且不需转向支承，同时为了节省造价，在主缆分散锚固起点处仅设置了散索套。散索套是一种简单的索股散开方式，但其形成的过程较为复杂，导致出现了以下不良后果:一是散索套中面以上的索股是往上偏转的，本身处于不稳定状态，索股架设的位置难以保证;二是散索套无法事先成型，索股架设到位后安合施工难度大，且难以同时保证索股的位置和拉力。加之以往的索股索力调整是通过改变锚头垫片的数量，垫片的厚度决定了最小调整量。因此以往此类悬索桥施工控制以线形控制为主，不对索股张力进行特别控制。由此导致的锚跨索股在成桥时出现的索力不均匀性，势必会影响到主缆的安全［2］。因此加强对此类大桥锚跨索股的分析，精确地计算锚跨索股的架设索力是确保悬索桥锚固系统合理性的关键。

以往锚跨分析研究多是针对散索鞍［3］，对于散索套则研究尚少。笔者根据板式加劲梁悬索桥的结构特点，提出了针对散索套的锚跨索力计算模式，并提出了此类桥型锚跨控制的新方法，即索股架设阶段按边锚跨索力相等进行安装、成缆后按精确理论计算值进行索力调整。根据此方案对在建中的乌江大桥进行控制，得到一些结论。

1 散索套组成和构造

散索套设置在主缆边跨与锚跨段相交的理论散索点上，功能类似于散索鞍，但结构构造上更类似于索夹［4］。主缆索股从喇叭形的小端进入散索套，从大端散出后直接连接锚面上的各个锚固点。散索套总体上分为两个功能区，大端为散开区段，其作用是约束主缆索股的散开方向，并将各个索股平顺地引入各自的锚固点。小端为夹紧区段，其作用是提供足够的夹紧力和抗滑摩阻力，从而使主缆上的理论散索点不发生改变。散索套一般情况下仅仅固定在主缆上，并随主缆运动，而不与其他固定结构物有关联。

与散索鞍不同，主缆中心线以上的索股经过散索套后是向上的，而在全部索股架设完成后，散索套才能闭合安装。因此，主缆索股安装时必须采取特殊措施，以保证主缆边跨线形的准确性。乌江大桥在主缆架设前安装临时散索支承架，用以固定理论散索点的高程及方便主缆索股的安装。散索套及临时散索支承架构造见图1。

2 锚跨索股计算

悬索桥锚跨的总体计算思路是通过确定合理的成桥状态得到各个索股的无应力长度，以此为前提进行成缆状态的计算。锚跨索股张力的计算必须考虑到散索套与索股的接触问题，即精确计算索股在散索套内的切点以及转角，同时还要考虑到从切点到锚固点的索股是一铅垂面上的悬链线，其在水平面上的投影为一直线［5］。数值分析方法是悬索桥计算的一个实用的方法，具有计算精度高、速度快、能方便模拟接触问题的优点。因而本文采用数值分析法。

图1 散索套结构图

2.1 成桥状态索力分布模式

锚跨是悬索桥主缆受力较大甚至是最大的位置，成桥时锚跨索力的分布情况将决定锚跨索股或者主缆的实际安全系数，因此需要事先确定锚跨索股的索力分布情况［6］。

在理想的成桥状态，散索套达到设计位置，并且处于悬浮状态。散索套以及两侧的索股在总体上满足平衡条件。由于散索套自身的重量相对于成桥状态下的索股索力较小，此处忽略了它的影响。针对散索套，本文介绍了两种锚跨索股成桥状态索力的合理分布模式。

模式一:锚跨各索股在与散索套的切点处的索力相等。切点处的索力是锚跨索股的最大索力，这种分布情况下，各索股的安全系数相同。

模式二:锚跨各索股与散索套切点处索力在主缆中心线上的投影分量相等。由此得出的索股索力不全相等，但一般情况下索力偏差较小，因此也是合理的。

工程实例表明此类悬索桥的锚跨索股布置是轴对称的，因此成桥状态下散索套的平衡条件为两侧索股索力沿散索套轴线方向投影相等。

结合上述条件可以求得唯一的锚跨索股的索力。

2.2 锚跨索股无应力长度计算

锚跨内主缆索股为分散锚固，同时具有平弯转角和竖弯转角两个未知数。本文充分考虑到使用散索套情况下锚跨索股的布置情况，作了如下假设:锚跨内各索股均与主缆中心线共面。这样一来就可以通过坐标系转换(图2)的方式减少一个未知数，即在索股所在平面内计算只需找到竖弯转角β。

由于索股和散索套的位置是确定的，所以竖弯转角β是唯一的。通过迭代求解便可以得到β值以及索股的空间曲线长度，再结合上文的索力分布模式得到索股切点处的索力，即可求得索股的无应力长度。具体流程见图3。

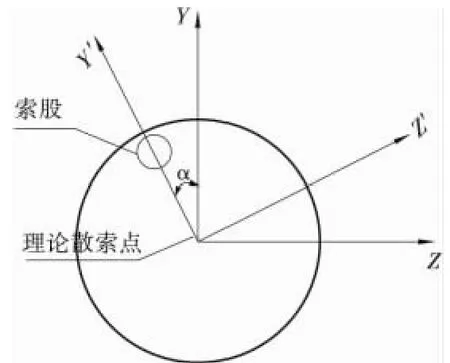
图2 索股分析图

图3 无应力长度计算流程

2.3 成缆状态锚跨索股索力计算

成桥状态下主索鞍和散索套处于设计位置，边跨主缆和锚跨索股满足散索套平衡条件。但在成缆状态下，为保证散索套的受力平衡，需对散索套设置预偏量［7］。该预偏量可以通过无应力长度不变原理以及散索套处的力学平衡等条件进行求解。实际工程中通常使用临时支承架保证散索套准确定位在预偏后的空间位置。有了固定的散索套位置，再结合上文得到的无应力长度计算结果，就能通过迭代算法程序得到成缆状态下锚跨各索股索力。

首先介绍计算中使用到的几个坐标系［8］(参见图4):成缆状态下以散索套轴线为坐标轴的成缆坐标系Xc—Yc—Zc;以成桥状态理论散索点为圆心的全局坐标系Xq—Yq—Zq;前文使用过的成桥状态锚跨坐标系X—Y—Z;在前述坐标系上加撇号代表的是该坐标系绕x轴旋转后得到的新坐标系。

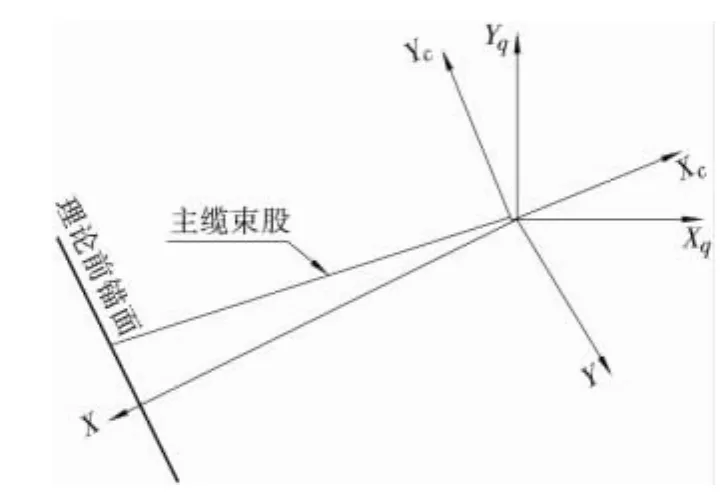
图4 锚跨计算坐标系

通过成缆坐标系的旋转，将待分析的索股放入特定平面内求解，得到索股有应力长度以及切点坐标(Xc'，Yc')，结合此索股的无应力长度可以得到初估的索股索力，进而求得索股切点之外的自由段的无应力长度。然后将此坐标换算到全局坐标系下得到(Xq，Yq，Zq)。有了索股自由段两端点坐标和无应力长度，就可以解得索股切点处的索力。最后比较切点处索力与初估值，若误差小于允许值则结束该索股的计算，否则修正初估索力进入下一个迭代循环直至收敛为止。具体流程见图5。

3 计算实例

3.1 工程背景

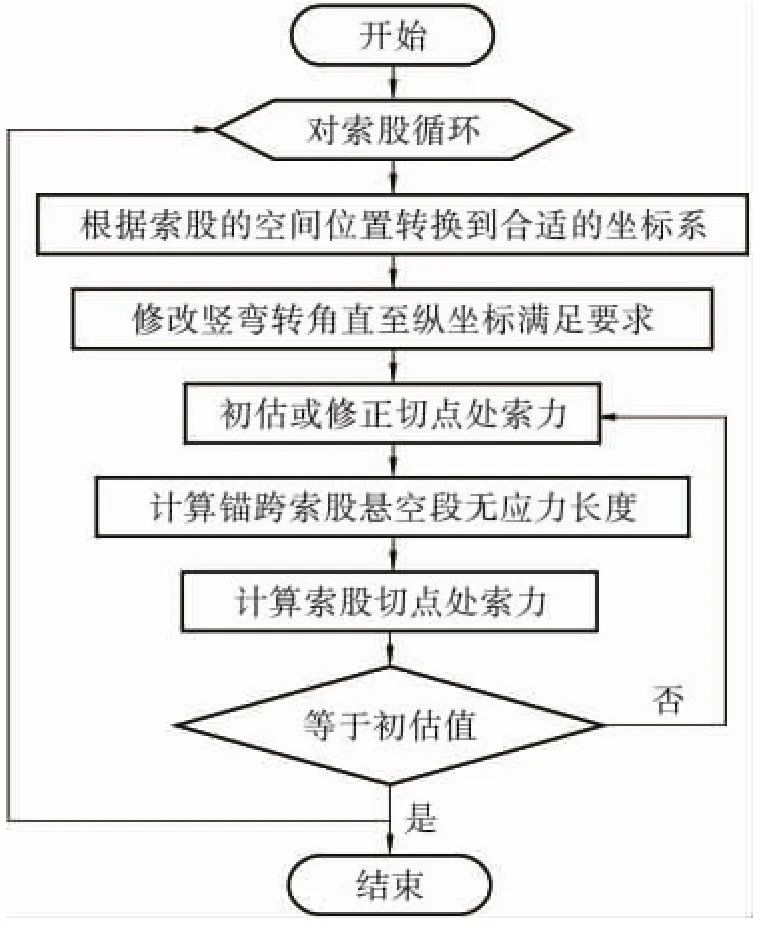
图5 成缆状态锚跨计算流程

贵州乌江大桥主跨为325 m，息烽侧边跨85 m，金沙侧边跨70 m，主缆矢跨比1/10。中跨为悬吊结构，两侧边跨无吊杆。主缆采用预制平行钢丝索股，全桥共2根主缆，每根主缆由37股索股组成，每股由127根直径为5.1 mm镀锌高强钢丝组成［9］。

计算参数包括:基准温度采用15℃;锚跨索股荷载集度q=0.199 6 kN/m;弹性模量E=2.0×105MPa;索股截面积 A=2.594 3 ×10－3m2。

3.2 计算结果

依据本文的分析方法编制了悬索桥锚跨索股计算程序［10］，对该桥的息烽侧锚跨索股进行了分析。在主缆架设完成后，记录了两岸锚跨索股张力的实测值，这里仅列出息烽侧下游锚跨的部分数据进行对比(见表1)。从表中可以看出，两种模式下求得的索力相差不大，所得索股无应力长度最大相差2 mm，同时和设计值吻合较好也证明了本文计算分析的正确性。

表1 乌江大桥锚跨分析结果

成缆状态下部分索力实测值和计算值吻合，但也有小部分索力实测值和理论计算值存在较大差距，其主要原因有:散索套安合时挤压主缆中心线以上的索股;实测时的索股温度与基准温度有差距;锚跨索股实际的边界条件并不是理想的铰接;索力测试的精度等［2］。其中第一条原因的影响较大且无法精确预估，因此必须等到散索套整体安装完成后对索股索力进行调整。考虑温度对锚跨索股索力的影响可参见文献［5］。

根据以上分析，模式1和2计算结果与设计相符，说明两种模式都是合理的。在实际的主缆架设过程中，可以按索股在散索套两侧索力相等的原则进行锚头安装，待安合散索套后再进行锚跨索股索力的调整。这样既能够保证边跨主缆的线形，也可以控制锚跨的索股索力在合理范围，有效提高主缆的安全系数。

4 结语

1)分析结果表明，针对板式加劲梁悬索桥提出的成桥状态锚跨索股索力的两种分布模式都是合理的，实际工程中可以任意选用。

2)充分考虑了此种桥型锚跨索股的分布特点，并根据索股无应力长度不变的原则，建立了成缆状态下的锚跨张力计算程序。

3)以乌江大桥为工程背景，将本文方法计算结果与之进行对比，验证了本文方法的正确性。提出的锚跨控制方法给实际施工提供了参考。

［1］徐恭义.板式加劲梁悬索桥［M］.成都:西南交通大学出版社，2010.

［2］许汉铮，黄平明.大跨径悬索桥主缆锚跨张力控制［J］.长安大学学报，2002，22(5):32－34.

［3］沈锐利，薛光雄.悬索桥主缆索股锚固力的计算方法探讨［J］.桥梁建设，2003(6):25－29.

［4］孟凡超.悬索桥［M］.北京:人民交通出版社，2011.

［5］谭红梅，葛 凯，曾 勇，等.悬索桥锚跨索股张拉力监控［J］.铁道建筑，2010(8):43－46.

［6］罗喜恒，肖汝诚，项海帆.悬索桥锚跨索股分析研究［J］.公路交通科技，2004，21(12):45 －53.

［7］唐茂林，沈锐利，强士中.大跨度悬索桥丝股架设线形计算的精确方法［J］.西南交通大学学报，2001，36(3):303 －307.

［8］肖 军，张永水，董 义.悬索桥锚跨索股分析及程序实现［J］.重庆交通大学学报(自然科学版)，2011，30(5):907－910.

［9］张 伟，曹洪武，易伦雄.贵州乌江大桥主桥设计［J］.桥梁建设，2013，43(2):81－86.

［10］彭国伦.Fortran95程序设计［M］.北京:中国电力出版社，2002.