基于智能容错算法的多传感器皮带秤

籍晋鹏， 李丽宏

(太原理工大学 信息工程学院，山西 太原 030024)

0 引 言

在现行皮带秤重量信息的采集中，由接线盒中将多路称重传感器并联连接，获得多路传感器信号之和,这种方式割裂了传感器之间的联系和相关性。由于称重传感器容易受使用环境的影响而损坏[1],所以,任何一路传感器出现故障都将导致称重系统失效。

根据传感器的对称分布提出了用对应传感器值代替故障传感器的方法[2],但由于皮带秤物料加载时物料下落位置的随机性和流量大小存在不确定性，难以保证物料在皮带秤上的对称分布，所以,这种方法也有着明显的缺陷。径向基函数神经网络(radial basis function neural network,RBFNN)[3]由于具有很强的逼近性非线性函数能力,利用对称分布的传感器之间存在着某种非线性函数关系[4,5]，本文提出以RBFNN为核心建立预估网络，模拟故障传感器的正常输出，完成在称重传感器失效情况下的皮带秤称量[6]。

1 皮带秤称重原理

全悬浮式秤架与非自动平台秤类似，称重平台由4只称重传感器支撑，称重托辊装在平台上。皮带秤结构与受力曲线如图1。

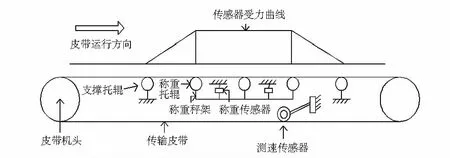
图1 皮带秤称重结构

在现行使用的皮带秤中，重量计量方法基本上可以分为两类，通常采用积分法或累加法来计算瞬时流量和累计重量。以下简述两种不同方法。

1)积分法

当皮带输送物料时，连续测量称重托辊上代表单位皮带长度上的载重值q(kg/m)，并将q值与同一时刻的皮带速度值v(m/s)相乘，则所得的乘积等于物料的瞬时流量

Q=qv,

(1)

式中Q为物料的瞬时流量值，kg/s。

T时间内的累计值Q(t)是瞬时流量Q对时间的积分值，即

(2)

式中q(t)为瞬时载重值；v(t)为瞬时皮带速度值。

2)累积法

累积计量法，是以采样时刻称重值和采样时刻皮带速度，估算整个采样周期内的累计量,即

(3)

将累计量对时间微分，可求出瞬时流量,即

(4)

受限于单片机无法进行复杂的积分运算，所以,采用累加法近似计算瞬时流量值和累计重量值。称重显示控制器将获得的传感器mV级电压信号由A/D转换为无量纲的数字量，即重量内码D。

在现行的皮带秤中采取信号简单的相加法来计算总重量内码D，即

(5)

由式(5)可以看出,任何一路传感器故障所导致的信号缺失、信号异常都会对称量值产生严重影响。

2 RBFNN智能容错算法

故障传感器的判断方法有很多种。根据文献[7]中所提到的传感器容错算法，设计了如图2的智能容错算法。

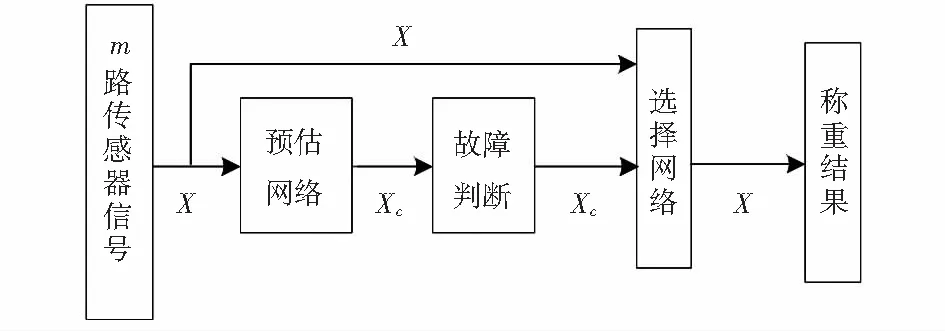
图2 智能容错判断

由图2可知，皮带秤系统分别独立采集m路称重传感器的重量内码X(x1,x2,x3,…,xm)。首先经过估计网络求得预估信号Xc(x1c,x2c,x3c,…,xmc)，并将2路信号X和Xc用于传感器故障判断[8]。若传感器无故障，直接由X计算得出称重结果；如果传感器故障，设第i只传感器故障，由预估信号xic代替原重量内码xi融合成新的重量内码X(x1,x2，…xi-1,xic,xi+1，…，xm)，再得出称重结果。

2.1 多传感器的相关性

多传感器的相关性是进行神经网络预估的基础。皮带秤多路传感器按一定的拓扑结构分布在皮带秤承载架下方，构成典型的多传感器系统，各只传感器相互关联，存在某种函数关系[9]

(6)

由式(6)表明：传感器xi的输出是其他m-1路传感器的输出函数。

2.2 预估网络

利用RBFNN逼近式(6)的多传感器关联函数，从而完成任一传感器的输出估计，广义神经网络模型如图3所示。

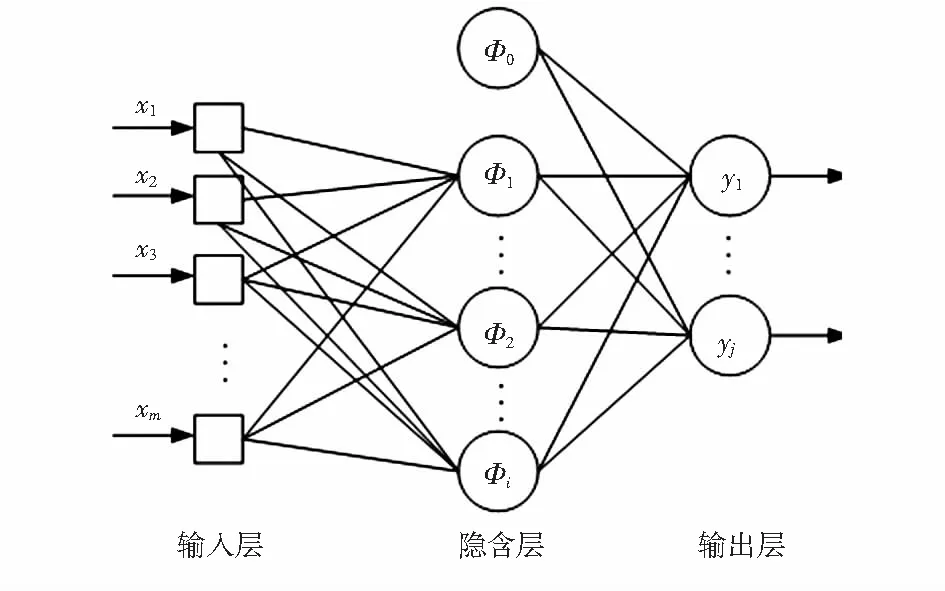
图3 广义神经网络模型

在人工神经网络中，节点对应图中的节点，权值表示节点之间的相互关联强度。网络将知识存储在调整后的各权值中，所以,权值的求取是整个神经网络的关键[10]。

预估计输出Xc(x1c,x2c,x3c,…,xmc)，其值为

(7)

隐含层基函数为高斯函数

(8)

其中,‖xk-xj‖为欧几里德距离，且

‖xk-xj‖2=

(9)

式中W为RBFNN的权重，W=[w1,w2,w3,…,wm]T，其中，w0=1。标准差σ按照下式选取

(10)

式中dmax为所选取的中心最大距离，n为隐含节点的个数。

用伪逆法求得输出权值W，在这里期望输出为原始数据中d={xij}。xij为第i个输入向量在第j处的期望输出值。wij(i=1,2,3,…,I;j=1,2,…,J)为第i个隐含节点到第j个输出节点的权值，则输出权值可用下式求出

W=G+d.

(11)

其中,G+={gkj},矩阵W=wij

(12)

2.3 故障判断

该诊断率只考虑在同一时刻只有一只传感器故障的情况,当n只传感器均正常时满足

(xi-xic)/xi<ε,i∈[1.n]，

(13)

式中ε为检测阈值。当任一传感器故障时，预测输出与自身输入有较大的误差

(xi-xic)/xi>ε.

(14)

连续采样k次后,如果仍然满足上式，则假设成立;否则，判定第i只传感器失效。本文以第3路称重传感器为实验对象，其他称重传感器用同样的方法。根据实验经验获得检测阈值ε为0.01，检测次数k为5。

3 预估网络训练和模拟

RBFNN采用有监督学习方式。每一个样本都对应一个教师信号作为期望输出，训练时计算实际输出与期望输出之间的误差，再根据误差的大小和方向对网络权值进行调整。误差可以使用各输出节点的误差均方值来衡量。这样就建立了一个以网络权值为自变量，最终误差性能为函数值的性能函数，网络训练转换为求解函数最小值的问题。

本文利用Matlab神经网络工具箱中的NEWRB函数自动构建的神经网络[11],结构如图4所示。

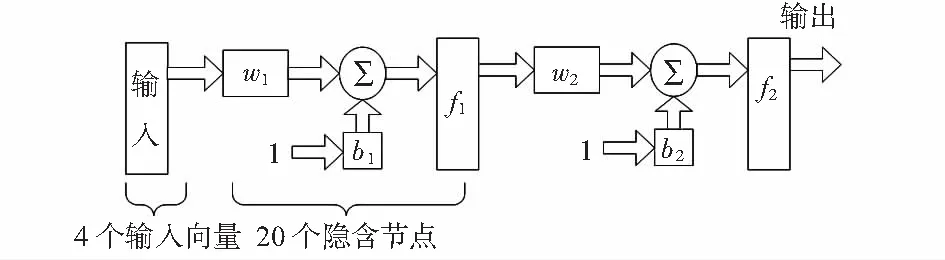
图4 径向基神经网络结构

RBFNN有不同的中心确定方法，在此处采用随机选取固定中心进行网络训练[12],能防止径向基函数出现太平或太尖的情况。

在随机选取固定中心的方法中，基函数的中心和标准差都是固定的，唯一需要训练的参数就是隐含层与输出层之间的权值。

在本文中采集20组检测数据用于神经网络训练。此时，RBFNN为一个4输入，4输出的广义RBFNN，该神经网络共有4个输入节点，隐含层有20个节点。模拟四路传感器称重量内码X[4,20]，数据如表1。

经数据预处理后，得到X=[x1,x2,x3,x4]。其中设定第3路传感器为故障传感器，并且以x3为目标输出进行神经网络的拟合检验。

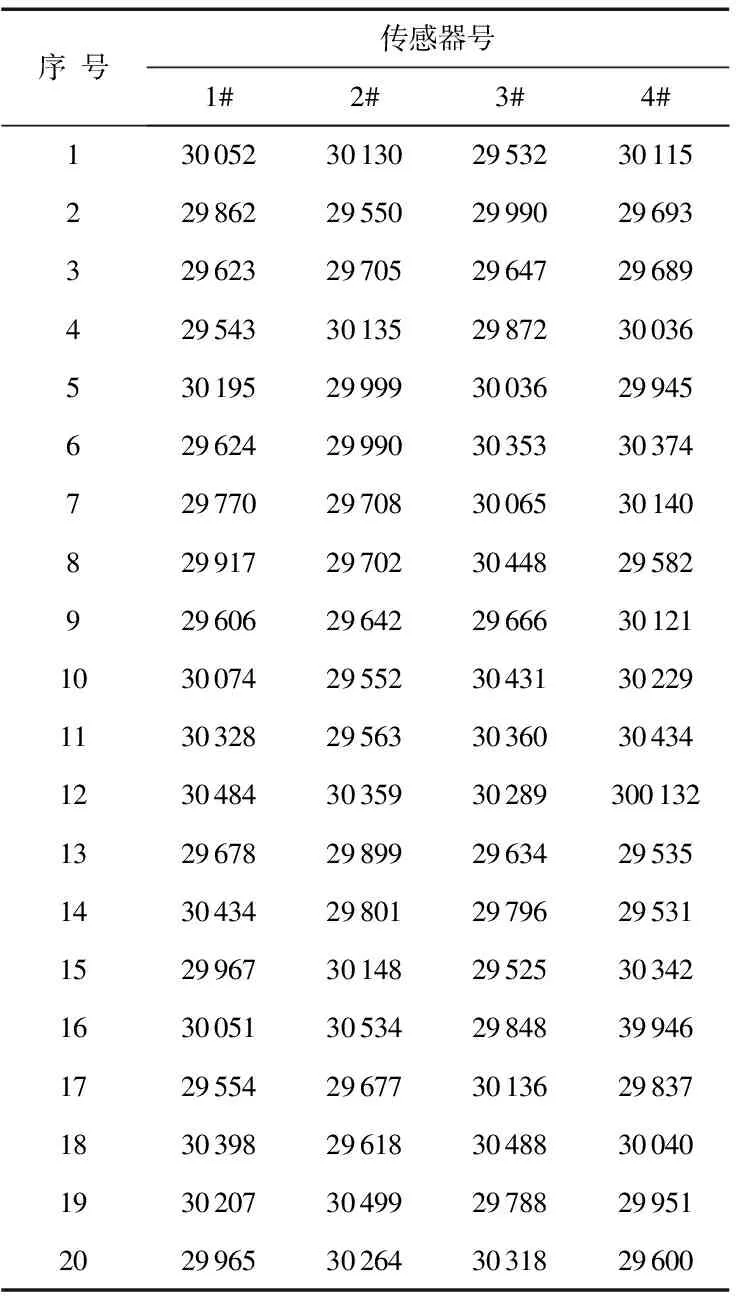
表1 模拟数据

由训练结果可见隐含神经节点的个数和MSE下降的过程。NEWRB,neurons=20,MSE=6.824 24×10-24,误差性能曲线如图5所示。

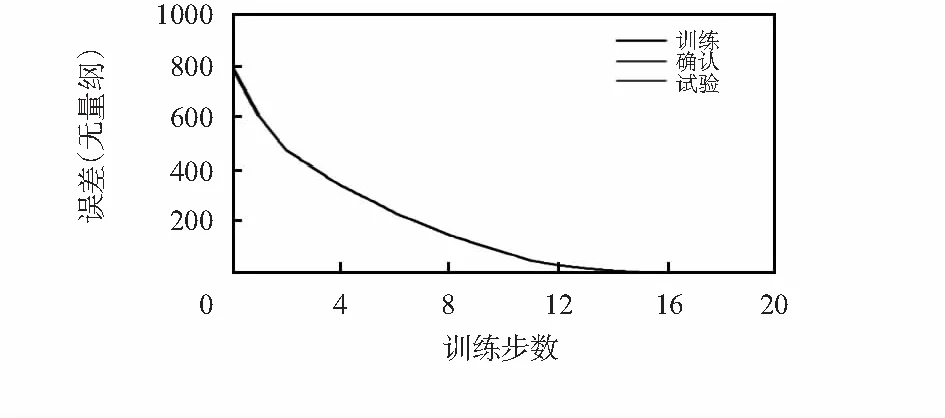
图5 性能误差曲线

从图6可以看出:当传感器正常时的称重数据和传感器发生故障后的称重结果有着明显的误差。用RBFNN预估计值xic拟合预故障传感器完成称重，以达到减少称重误差的作用。

4 结 论

基于神经网络的信息融合技术应用于故障传感器的诊断，目的是将神经网络的非线性拟合能力与多传感器系统中相关传感器之间的信息冗余特性有效结合起来，准确地判断出传感器的故障，并对故障传感器的信号进行模拟恢复。本文将RBFNN应用于电子皮带秤能有效地解决在生产中由于传感器故障发现不及时而导致的称重误差。

参考文献:

[1] 王传文.称重传感器的工作原理及故障检测[J].化学分析计量,2002,11(4):40-41.

[2] 林海军,滕召胜,迟 海，等.基于多传感器相关性的汽车衡智能容错方法[J].仪器仪表学报,2009,30(11):2336-2341.

[3] 林海军,滕召胜,迟 海，等.基于RBF神经网络的汽车衡误差补偿[J].湖南大学学报:自然科学版,2010,37(5):40-44.

[4] 安百旺,葛方远.浅谈称量台式电子皮带秤称重传感器的选型及其安装位置[J].科技信息,2011(10):I0315-I0315.

[5] 张娅玲,陈伟民,章 鹏,等.传感器故障诊断技术概述[J].传感器与微系统,2009,28(1):4-6.

[6] 唐家德.基于Matlab的非线性曲线拟合[J].计算机与现代化,2008(6):15-19.

[7] 房 方,魏 乐.传感器故障的神经网络信息融合诊断方法[J].传感技术学报,2000,13(4):272-276.

[8] 许秀玲,汪晓东.传感器故障诊断方法研究[J].佛山科学技术学院学报:自然科学版,2004,22(3):18-22.

[9] 林海军,滕召胜,刘让周,等.基于自适应加权融合的汽车衡故障传感器预估[J].仪器仪表学报,2010(7):1509-1513.

[10] 陈 明.Matlab神经网络原理与实例精解[M].北京：清华出版社，2013：196-242.

[11] 张秀玲,张志强.四种确定RBFNN中心的新算法[J].工业仪表与自动化装置,2007(2):6-9.

[12] 李 萍,曾令可,税安泽,等.基于 Matlab 的 BP 神经网络预测系统的设计[J].计算机应用与软件,2008,25(4):149-150.