基于反演的稳定高效衰减补偿方法

王本锋，陈小宏，李景叶，陈增保，刘国昌

1中国石油大学（北京）油气资源与探测国家重点实验室，北京 102249 2中国石油大学（北京）CNPC物探重点实验室，北京 102249

1 引言

通过衰减补偿获得高分辨的地震资料，有利于地层或岩性解释，提高油气藏检测或储层反演的精度，是地质学家和地球物理学家共同关注的热点问题之一.地震波在地下介质中传播时，由于地下介质的黏滞性以及非均匀性，经历了大地的Q值滤波过程，使得子波的高频成分迅速衰减，垂向分辨率降低（Hargreaves and Calvert，1991；Varela etal.，1993）.很多衰减模型都可以用来描述地震波的衰减过程，Toverud和Ursin（2005）利用零偏VSP数据比较了八种不同的衰减模型，效果相当，但是最常用的衰减频散模型为Kolsky-Futterman模型.基于该模型，Wang（2002，2006）在波场延拓的基础上推导了具有大地滤波效应的衰减补偿公式以及正Q滤波公式；Wang（2011）在爆炸反射面的基础上推导了正Q滤波公式；Zhang和Ulrych（2007）利用贝叶斯理论和最小二乘反演策略，实现了衰减补偿过程，得到了高分辨率的反射系数序列.

反Q滤波过程可看成逆波场延拓或偏移的过程，消除大地Q值滤波的影响.相位校正是无条件稳定的过程，但振幅补偿具有不稳定性，可以用振幅增益限制或其他稳定性方法解决.Hale（1991）指出，在反Q滤波过程中，波场的直接显式外推方法不稳定，能量随着深度的增加呈指数增加；隐式外推方法一定程度上是稳定的，但是计算量大，效率低，难以向多维推广，因此设计稳定的显式外推方法成为关键问题.Hargreaves（1992）分析比较了一些简单的反Q滤波方法，为利用滤波器的相似性质实现反Q滤波奠定基础.赵建勋和倪克森（1992）借鉴串联偏移的思想，将常Q算法推广到深变Q模型；将串联频散补偿算法与限幅补偿算法相结合，更好地改善地震资料的分辨率.Wang（2002，2006）在波场延拓的基础上，推导了反Q滤波公式，由于振幅补偿的不稳定性，提出了增益限制以及稳定性方法；Yan和Liu（2009）将该稳定性方法推广到转换波中，实现了叠前反射纵波以及PS转换波的反Q滤波，但是该稳定性方法对高频成分没有起到补偿作用，以致在Q值较小时，不能起到很好的补偿作用.余振等（2009）对反Q滤波方法进行了详细研究，根据其实现形式将其分为三类：用级数展开作近似高频补偿的反Q滤波方法、基于波场延拓的反Q滤波方法以及其他的反Q滤波方法，并对其稳定性进行了分析.Wang（2011）在爆炸反射面的基础上，利用正Q滤波公式，借鉴反演的思想实现了地震记录的衰减补偿；忽略子波的影响进行求解，即可实现补偿的过程，但物理解释困难.Zhang和Ulrych（2007）利用贝叶斯理论和最小二乘反演策略，实现了补偿的过程，得到了高分辨率反射系数序列，但是它只是利用时变子波与反射系数进行褶积得到地震记录，由于此方法涉及子波的提取过程，若子波提取不准，其误差会影响反射系数反演的精度.姚振兴等（2003）研究了深度域衰减补偿方法，因为深度域地震剖面是石油地震勘探的最终成果.

反Q滤波的过程需要知道Q的信息，常规的Q值提取方法有频谱比法、上升时间法等（Zhang and Ulrych，2007）；赵伟和葛艳（2008）在小波域利用零偏移距VSP资料对Q值提取进行了分析.由于Q值求取困难，但其可利用Gabor变换，通过非稳态反褶积提高地震记录的分辨率，避开求取Q值的过程，直接求取反射系数，得到高分辨的地震资料（Margrave etal.，2011）.但是它要求子波以及衰减函数都是最小相位的，而实际资料一般为混合相位，假设偏离实际，会导致其在实际资料处理中失效.

本文基于波场延拓正Q滤波公式，借鉴反演的思想，实现地震记录的衰减补偿，最终得到高分辨的地震记录.由于反问题求解是一个不稳定的问题，这也诠释了衰减补偿是一个不稳定的过程；反问题的求解可通过正则化方法进行，最终得到补偿后的地震记录.该过程避免了常规反Q滤波方法振幅补偿不稳定的缺陷，改善了振幅增益限制方法以及稳定的反Q滤波方法对Q值较小时欠补偿的局限.

2 方法原理

在波场延拓的基础上，Wang（2002）推导了反Q滤波公式，

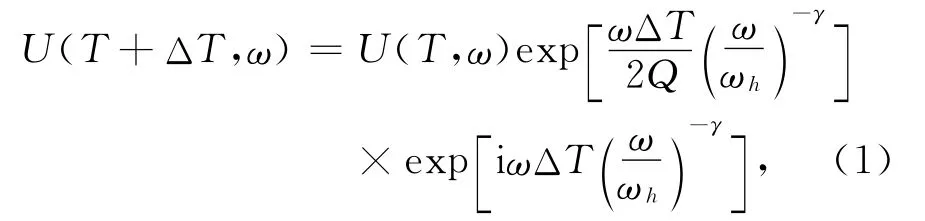
式中的两个指数项分别为对振幅以及相位的校正项.振幅校正项随着时间和频率的增加呈指数增加，这是导致振幅补偿不稳定的原因.鉴于其不稳定性，Wang提出了增益限制方法和稳定性方法，限制对高频信号的补偿.设振幅补偿项为

则增益限制方法对该补偿项修改为

整理公式（1），再利用其递推关系式得

比较稳定反Q滤波方法与振幅增益限制方法，对无噪数据，两种方法都能对衰减的记录起到稳定化补偿的作用，但在Q值较小的情况下，均表现为补偿不足；对含噪数据，增益限制会出现不稳定情况，稳定的反Q滤波方法的补偿效果表现为欠补偿.

鉴于振幅增益限制方法以及稳定的反Q滤波方法对Q较小情况下补偿不足的缺陷，本文结合Wang（2011）以及Zhang和Ulrych（2007）的思想，基于正Q滤波公式，利用反演的策略，实现地震记

录的衰减补偿.具有大地吸收效应的正Q滤波公式为（Wang，2008）

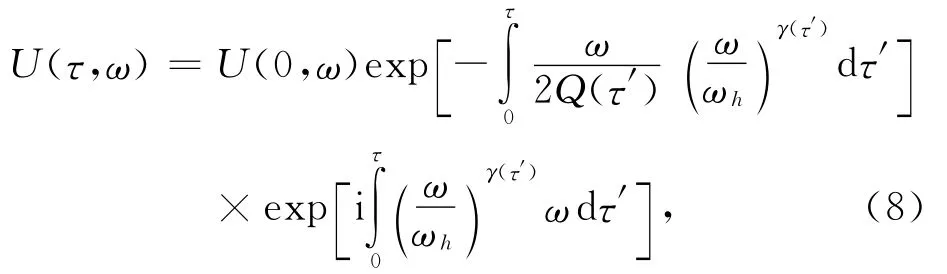
由于地震数据的带限性，一般在有效频带内求出有效频率成分.公式（9）可离散化写成方程组的形式，如公式（10）所示，

其中，S为衰减的地震记录，为实值序列；A 为包含衰减信息的复值矩阵；U为有效频带内未衰减的地震记录的频谱，为复数序列.将方程（10）转化为实值方程，如公式（11）所示，

简记为

其中，d＝S， L＝ ［Re（A），-Im（A）］， m＝［Re（U）；Im（U）］.由于地震数据频带有限以及噪声的污染，方程（12）的求解是不适定的.为此，考虑到地震数据频谱的光滑性，采用正则化策略以及L2范数约束，构建目标泛函如下：

其中，μ为正则化因子，D可以取为单位算子、一阶微分算子或二阶微分算子，其对应的解方程为

通过求解得到未衰减的地震记录的频谱，再经傅里叶逆变换，得到补偿后的地震记录.若已知子波的信息，可利用反褶积技术，得到高分辨的反射系数序列.

另外，也可直接反演得到补偿后的地震记录.由公式（9）得

将公式（15）离散化，得矩阵的形式，

其中，u1是衰减的地震记录，为实值序列；A是与衰减有关的复值矩阵；B是与傅里叶变换有关的复值矩阵；u2是未衰减的原始地震记录，为实值序列.将方程（16）改写为实值方程，

其中，L2＝Re（AB）.由于地震数据频带有限以及噪声的污染，方程（17）的求解是不适定的.为此，考虑到地震数据的光滑性，采用正则化策略以及L2范数约束，构建目标泛函如下：

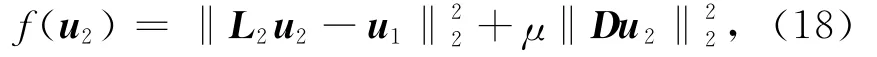
其中，μ为正则化因子，D可以取为单位算子、一阶微分算子或二阶微分算子.其对应的解方程为

通过求解方程（19），可直接得到补偿后的地震记录.

对比公式（14）与公式（19），公式（14）中待求解的参数为地震记录的有效频率分量，而公式（19）中待求解的参数为地震记录时间序列，相当于全频段的信息，计算量较大；且高频成分易被噪声干扰，不易处理.因此本文仅采用公式（14）对衰减问题进行分析求解，得到有效频带内的频谱，再利用傅里叶逆变换得到未衰减的地震记录.

3 数值算例

首先，对稀疏反射系数进行试验.设地下有5个反射界面，分别位于200ms、600ms、1000ms、1400ms、1800ms处，利用雷克子波（主频20Hz，采样率为2ms），首先合成无衰减的地震记录；其次，在Q值分别为400、200、100、50、25的情况下合成衰减的地震记录，如图1所示.

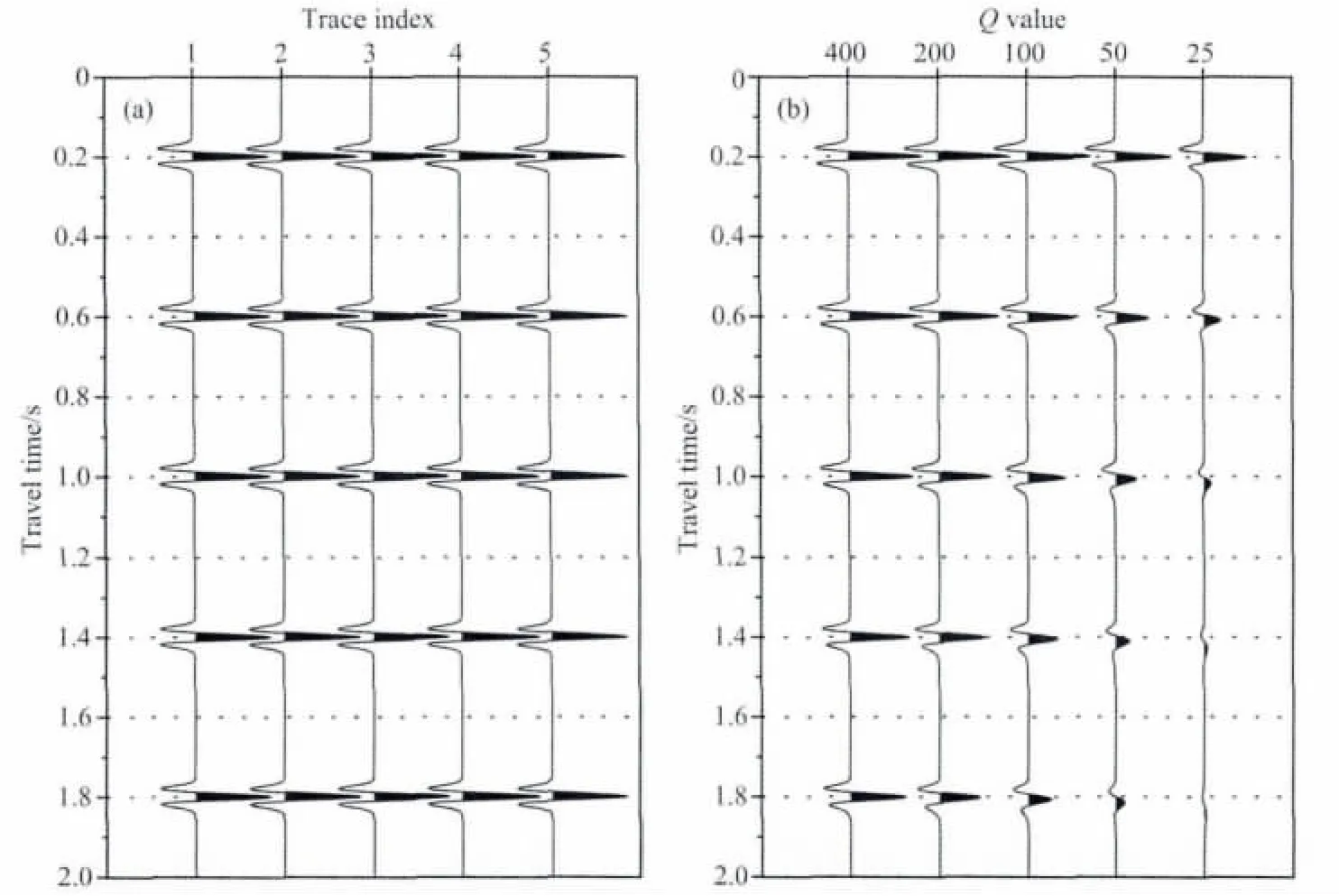
图1 （a）无衰减地震记录；（b）不同Q值对应的衰减记录Fig.1 （a）Seismic record without attenuation；（b）Attenuated record with different Qvalues

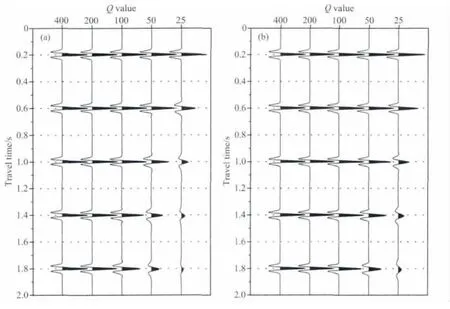
图2 （a）振幅增益限制方法以及（b）稳定化反Q滤波方法补偿结果Fig.2 Compensated results by the（a）gain-limited method and（b）stabilized inverse Qmethod

由图1b可以看出，随着Q值的减小，波衰减越快；传播时间越长，波形畸变越厉害.首先利用振幅增益限制方法以及稳定化的反Q滤波方法分别对衰减地震记录进行补偿，结果如图2a、2b所示；再利用本文方法对衰减地震记录进行补偿，D取为单位矩阵，求得阻尼最小二乘解，得到补偿后的地震记录如图3所示，另外D也可取为一阶微分算子或二阶微分算子.

图3 本文方法补偿结果Fig.3 Compensated results by the proposed method

由图2a、2b可以看出，在无噪声时，增益限制方法以及稳定的反Q滤波方法均能对衰减地震记录进行稳定性补偿，但在传播时间较长以及Q值较小时，均不同程度地表现出补偿不足；比较图2a、2b可知，稳定的反Q滤波方法补偿结果相对较好.本文方法只利用正Q滤波公式，借鉴反演的策略实现衰减补偿得到的记录，对振幅和相位进行了很好的校正，弥补了振幅增益限制方法以及稳定的反Q滤波方法对Q值较小时欠补偿的缺陷.该模型结果阐释了该方法的稳定性好、精度高的优点.

为了验证本文方法的抗噪性，对含弱随机噪声的地震记录进行处理.每道噪声的最大振幅与信号的最大振幅比为2%，由于噪声水平较小，在图上几乎观察不到.含噪记录、振幅增益限制方法补偿结果、稳定的反Q滤波方法补偿结果以及本文方法补偿结果如图4所示.

由图4可以看出，振幅增益控制方法在Q值较小时，振幅补偿的同时放大了噪声，出现了数值不稳定的情形；稳定的反Q滤波方法对噪声有一定的适应性，相对振幅增益控制方法，稳定的反Q滤波方法的实用性更强，但Q值较小时表现为欠补偿.本文方法对含噪地震记录能进行较好的补偿，补偿结果优于振幅增益控制方法以及稳定的反Q滤波方法.其关键在于正则化因子μ的选择，噪声水平较大时，选择较大的μ，会提高稳定性，但是会降低补偿效果，反之亦然.实际资料处理中，可通过反复试验，最终确定μ的取值.

图4 （a）含噪衰减记录；（b）增益控制补偿方法；（c）稳定的反Q滤波方法；（d）本文方法补偿后的记录Fig.4 （a）Noisy seismic records；（b）Compensated results by the gain-limited method；（c）Compensated results by the stabilized inverse Qmethod；（d）Compensated results by the proposed method

上述讨论的模型，反射系数为稀疏的，偏离实际情况，下面对随机产生的伪反射系数序列进行试验，一定程度上更接近实际情况.图5是反射系数序列以及利用雷克子波（主频30Hz，时间采样率为2ms）合成的无衰减的地震记录.

当Q值分别取400、200、100、50、25时，合成衰减地震记录如图6a所示，稳定的反Q滤波方法以及本文方法对衰减地震记录进行补偿，得到补偿后的记录如图6b—6c所示.分析图6可知，随着Q值的减少以及传播时间的增大，衰减越严重，且本文方法的补偿结果优于稳定的反Q滤波方法.对比无衰减的地震记录图5b以及稳定的反Q滤波方法图6b和本文方法图6c的补偿结果可知，本文方法的精度最高，基本消除了衰减的影响；克服了传统反Q滤波方法不稳定的缺陷，弥补了Q值较低时，稳定的反Q滤波方法补偿不足的局限性，其稳定性好、精度高、补偿效果好.

图5 （a）随机反射系数序列；（b）无衰减的地震记录Fig.5 （a）Random reflectivity series；（b）Seismic records without attenuation

最后，将本文方法应用于实际资料处理中，衰减补偿前的地震记录如图7a所示，从图上可以看出，地震记录的振幅发生衰减，相位发生畸变.利用稳定的反Q滤波方法以及本文方法对该记录进行补偿；基于常Q模型（Q＝100）得到衰减补偿后的地震记录如图7b—7c所示，分别为稳定的反Q滤波方法以及本文方法的补偿结果.通过比较图7a—7c知，地震记录的分辨率得到提高（同相轴变细且连续），振幅得到补偿、相位得到校正；特别是黑色圆圈以及箭头所指位置，同相轴更加清晰且连续，分辨率得到提高.图7a—7c对应的平均振幅谱如图8所示，通过分析振幅谱曲线可知，补偿后的地震记录的振幅谱得到展宽，本文方法以及稳定的反Q滤波方法均能达到提高分辨率的目的，且本文方法的补偿效果更好.但补偿后的归一化振幅谱曲线低频相对变弱，分析原因如下：

（1）由公式（9）可知，高频相对低频振幅值衰减较快，衰减补偿前，峰值频率较低，低频为优势频率；衰减补偿后，相位得到校正、振幅得到补偿，峰值频率向中高频移动、中高频相对低频振幅补偿较多，且高低频放大不成比例；

（2）实际Q值随频率变化，但本文采用常Q模型对衰减地震记录进行补偿，Q值不精确也是导致归一化的振幅谱低频相对变弱的原因之一.相对直接求解补偿后的地震记录而言，该方法只需求解有效频带内的频率分量，求解方程组的规模相对较小，计算效率较高，具体分析详见讨论部分.

4 讨论

本文方法具有较好的稳定性以及较高的精度，而且只计算有效频带内的频率分量，与直接计算未衰减的地震记录相比具有较高的效率.分析如下：设N为地震记录的长度，直接求解地震记录方法，要求解的方程组的规模为N×N，本文方法只需求解规模为2 M×2 M的方程组，其中M是有效频带内的频点数，一般情况下M＜N／4.例如，dt＝0.002s时，则奈奎斯特频率fn＝250Hz，假设地震数据的最高频率为fmax＝120Hz，则.用高斯消去法解方程组时，其计算量为，其中n为方程组的规模，从该计算量上可以看出，本文方法具有较高的效率.

Wang（2011）基于反演的衰减补偿，其求解的参数为反射系数序列，由上面的计算量分析可知，其计算量较大；其忽略子波的影响，即能起到补偿的作用，物理成因解释难.Zhang和Ulrych（2007）利用最小二乘的观点求解反射系数序列，计算量与Wang的方法相当，但是其正演记录为衰减子波与反射系数的褶积，它基于褶积机制，而不是接近实际的波动方程机制；其次，子波估计不准会对反射系数反演带来误差，影响反演的精度.本文的方法不涉及子波的问题，只起到衰减补偿的作用，来提高地震记录的分辨率，稳定性好、精度高，且具有较高的计算效率.

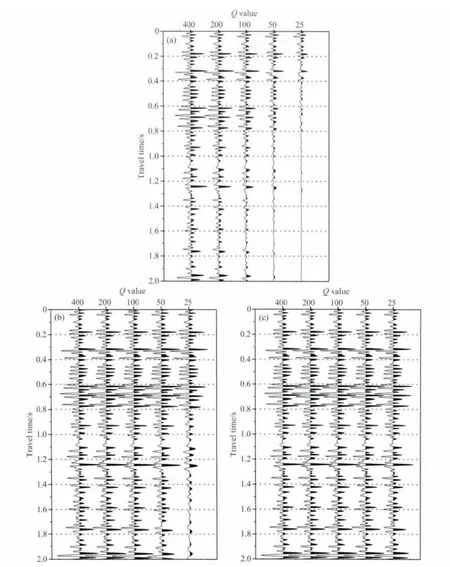
图6 （a）不同Q值对应的衰减地震记录；（b）稳定的反Q滤波方法；（c）本文方法衰减补偿结果Fig.6 （a）Attenuated seismic records with different Qvalues；（b）Compensated records by the stabilized inverse Qmethod；（c）Compensated records by the proposed method

本文的模拟实验以及实际数据处理都是在Q值已知的情况下进行的，且Q为等效Q值.但是其可推广到层Q以及连续变化的Q情形，再利用本文的方法进行求解.但是，Q值的精确提取是一个比较困难的工作，Q值估计误差会影响本文方法的处理效果，因此高精度的Q值提取方法，如基于全波形反演的Q值估计成为热点；再者，不直接求取Q值而实现提高分辨率目的的非稳态反褶积，也逐渐成为了研究趋势.

5 结论

图7 （a）补偿前的地震记录；（b）稳定的反Q滤波方法；（c）本文方法补偿后的地震记录Fig.7 （a）Seismic records before compensation；（b）Compensated results by the stabilized inverse Qmethod；（c）Compensated records by the proposed method

本文基于大地滤波的正Q滤波机制，借鉴反演的思想讨论了一种新的衰减补偿方法，可以得到补偿后的地震数据.该方法克服了传统反Q滤波方法不稳定的弊端，改善了振幅增益限制方法以及稳定的反Q滤波方法补偿不足的局限，具有稳定性好、精度高的优点；与其他直接反演地震记录时间序列的方法相比，其只需求解有效频带内的频率成分，具有较高的效率；且该方法可以推广到层Q以及Q值连续变化的情况，对振幅和相位同时进行校正.模拟实验以及实际数据处理效果均验证了本文方法的有效性.

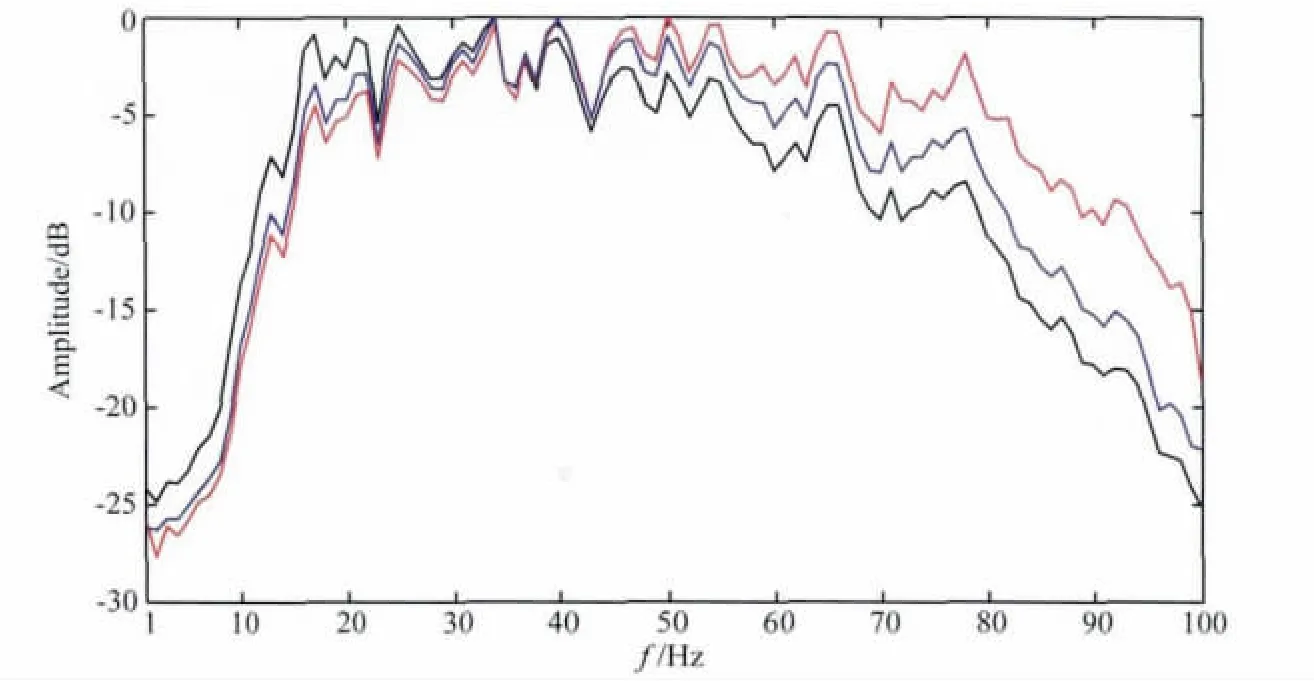
图8 地震剖面的平均振幅谱对比黑线对应图7a，蓝线对应图7b，红线对应图7c.Fig.8 Comparison of average amplitude spectra of seismic data Black line corresponds to Fig.7a；Blue line to Fig.7b；Red line to Fig.7c.

Hale D.1991.Stable explicit depth extrapolation of seismic wavefields.Geophysics，56（11）：1770-1777，doi：10.1190／1.1442989.

Hargreaves N，Calvert A.1991.Inverse Qfiltering by Fourier transform.Geophysics，56（4）：519-527，doi：10.1190／1.1443067.

Hargreaves N D.1992.Similarity and the inverse Qfilter：some simple algorithms for inverse Qfiltering.Geophysics，57（7）：944-947，doi：10.1190／1.1443307.

Margrave G F，Lamoureux M P，Henley D C.2011.Gabor deconvolution：Estimating reflectivity by nonstationary deconvolution of seismic data.Geophysics，76（3）：W15-W30，doi：10.1190／1.3560167.

Toverud T，Ursin B R.2005.Comparison of seismic attenuation models using zero-offset vertical seismic profiling（VSP）data.Geophysics，70（2）：F17-F25，doi：10.1190／1.1884827.

Varela C L，Rosa A L R，Ulrych T J.1993.Modeling of attenuation and dispersion.Geophysics，58（8）：1167-1173，doi：10.1190／1.1443500.

Wang S D.2011.Attenuation compensation method based on inversion.Applied Geophysics，8（2）：150-157，doi：10.1007／s11770-011-0275-3.

Wang Y H.2002.A stable and efficient approach of inverse Q filtering.Geophysics，67（2）：657-663，doi：10.1190／1.1468627.

Wang Y H.2006.Inverse Q-filter for seismic resolution enhancement.Geophysics，71（3）：V51-V60，doi：10.1190／1.2192912.

Wang Y H.2008.Seismic Inverse QFiltering.Wiley-Blackwell.

Yan H Y，Liu Y.2009.Estimation of Qand inverse Qfiltering for prestack reflected PP-and converted PS-waves.Applied Geophysics，6（1）：59-69，doi：10.1007／s11770-009-0009-y.

Yao Z X，Gao X，Li W X.2003.The forward Q method for compensating attenuation and frequency dispersion used in the seismic profile of depth domain.Chinese J.Geophys.（in Chinese），46（2）：229-233.

Yu Z，Wang Y C，He J，etal.2009.A review of inverse Qfiltering methods.Progress in Exploration Geophysics（in Chinese），32（5）：309-314，325.

Zhang C J，Ulrych T J.2007.Seismic absorption compensation：A least squares inverse scheme.Geophysics，72（6）：R109-R114，doi：10.1190／1.2766467.

Zhao J X，Ni K S.1992.Cascaded inverse Qfiltering and the application.Oil Geophys.Prosp.（in Chinese），27（6）：722-730.

Zhao W，Ge Y.2008.Estimation of Qfrom VSP data with zero offset in wavelet domain.Chinese J.Geophys.（in Chinese），51（4）：1202-1208.

附中文参考文献

姚振兴，高星，李维新.2003.用于深度域地震剖面衰减与频散补偿的反Q滤波方法.地球物理学报，46（2）：229-233.

余振，王彦春，何静等.2009.反Q滤波方法研究综述.勘探地球物理进展，32（5）：309-314，325.

赵建勋，倪克森.1992.串联反Q滤波及其应用.石油地球物理勘探，27（6）：722-730.

赵伟，葛艳.2008.利用零偏移距VSP资料在小波域计算介质Q值.地球物理学报，51（4）：1202-1208.