一种新绝对QPSK非相干解调原理提出及仿真
贾志成,师嘉伟,李永军
(1.河北工业大学 信息工程学院,天津 300401;2.国家海洋技术中心 天津 300112)
一种新绝对QPSK非相干解调原理提出及仿真
贾志成1,师嘉伟1,李永军2
(1.河北工业大学 信息工程学院,天津 300401;2.国家海洋技术中心 天津 300112)
为消除卫星通信对接收机本身的振荡频率精度和稳定度的要求。提出一种不需载波恢复的绝对四进制移相键控(QPSK)非相干解调法。首先由四相波形的积分特性得出两路二元码波;然后根据两路二元波判决出调制前信息;最后估算出理想误码率。Matlab仿真结果表明,该解调方法具有可行性。由于不需要载波恢复或码变换器,与传统QPSK通信相比,该电路简单且无相位模糊问题。
卫星通信;绝对QPSK;非相干解调;误码率;Matlab
在卫星通信过程中,在通信双方处于相对运动状态或受到电离层等自然影响时,接收到的信号会产生一个频率漂移移,我们称这种频移为多普勒频移[1-2]。为解决多普勒频移,接收机必须随时跟踪信号频率[3-4]。现代频率跟踪器不仅无法在处理时间和硬件简化上获得统一,还在接收机本机的振荡频率精度和稳定度上有很高的要求[5]。适中的频谱利用率和同信噪比下的低误比特率特征的四进制移相键控(QPSK)调制方式已广泛用在数字卫星通信系统中。如今QPSK调制信号的解调方法只能在载波恢复与延迟相乘二选一,在某些条件下,设计和实现很是复杂[6]。文中提出一种无需载波恢复与延迟相乘的绝对QPSK解调器,该解调器可以简单、低成本地设计实现QPSK解调,并且无振荡频率精度、稳定度要求与相位模糊问题。
随着时代发展,现代通信卫星已成为集解调、译码、信息处理、星上多层网络通信交换于一体的一个终端[7]。本章提出的解调器,由于其结构简单、成本低廉,无论是对通信卫星系统的QPSK解调,还是对用于中继卫星与全球定位系统的非平衡QPSK(UQPSK)解调都提供了一种很好的选则[8]。
1 QPSK非相干解调原理
QPSK发送端已调信号时域表达式可以表达为:

绝对QPSK非相干解调器原理如图1所示:首先将接收到的QPSK信号移相π/2,并与原波相减和相加;其次分别对两波形积分;然后通过相减积分波加上相加波,相加积分波减去相减波,产生两个二元矩形波,从两个二元波形可以发现,相加后的二元波与 I(t)-Q(t)波形相同,相减后的二元波与-I(t)-Q(t)波形相同;最后通过判决两个二元矩形波,就可以获得绝对QPSK调制前的码信息。
现以载波0相绝对QPSK为例,设信号0、1、2、3分别是0、π、π/2和3π/2,载波频率与数字信号码元速率相等,现调制信号为 0123,图 1 中 A、B、C、D、E、F、G、H 点的波形如图 2中的 A、B、C、D、E、F、G、H 所示, 由图 2中 D 和 E 可以看出,D与E的波形相加后,四相均为常数,“0相”与 “π/2相”为正,“π相”与 “3π/2”相为负。由图 2中 C和 F可以看出,F减去C后的波形,四相全为常数,“0相”与“3π/2相”为正,“π/2相”与“π相”为负。得到的两二元矩形波,图1中的G、H点波如图2中G、H所示。


图2 解调器各点波形Fig.2 waveform of every demodulator points
由上文可知绝对QPSK非相干解调由于不需要码变换器及载波恢复器,所以电路简单易行且无相位模糊,有很好的成本优势。但必须注意,为使波E与波F相关码元采样同步,硬件应使用无延迟移相器与同步积分器,载波频率必须是码元频率整数倍和系统位同步器必须在多普勒频移下可工作[9]。
2 QPSK非相干解调误码率
现设信号幅度为 A,信道窄带高斯白噪声 n(t) ~(0,σ2),功率普密度为 n0/2,n(t)移相 π/2 后,其均值、方差、功率谱密度与 n(t)相同。 n(t)的积分为:

当 I(t)、Q(t)出现 A 与-A 的概率都为 1/4 时,图 1 系统波 G,G(t) ~N(I(t)-Q(t),2σ2+n0s),波 H,H(t)~N(-I(t)-Q(t),2σ2+n0s)其中s为一个周期内抽样时刻的时间,由于通信系统频率远远大于 1,故可以认为 G(t)~N(I(t)-Q(t),2σ2)H(t)~N(-I(t)-Q(t),2σ2+n0s)。 令 α(x)~N(A,2σ2)、β(x)~N(-A,2σ2),则波 G 或波 H 误码率为:

故总误码率为:

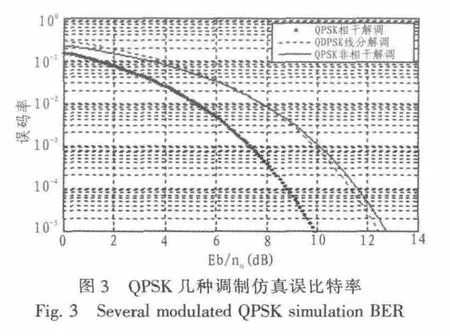
当噪声为均值为0的窄带高斯白噪声时,QPSK几种调制仿真误比特率如图3所示。
3 绝对QPSK非相干解调Matlab仿真
以载波0相绝对QPSK为仿真对象,当调制信号最大幅度A=1 V,码速率10 baud,载频20 Hz,仿真离散点最大频率1 000 Hz,信噪比为12 dB时,随机发送信号、调制信号、加噪调制信号、解调信号由上到下如图4所示。

图4 无偏移10 baud调制解调波Fig.4 No phase shift 10 baud modulation and demodulation waves
由图4知,加入噪声后,调制信号可以被正确的还原。当图4随机信号码速率变为20 baud,载频变为40 Hz时,随机发送信号、调制信号、加噪调制信号、解调信号由上到下如图5所示。

图5 无偏移20 baud调制解调波Fig.5 No phase shift 20 baud modulation and demodulation waves
由图4和图5比较看出,无论信号频率如何变幻,只要能正确提取位定时,绝对QPSK非相干解调都可以还原信号,即具有抗多普勒频移能力。当对图4随机信号载波加入π/8相位偏移时,随机发送信号、调制信号、加噪调制信号、解调信号由上到下如图6所示。
由图4和图6比较看出,绝对QPSK非相干解调系统不但具有抗多普勒频移能力,还具有很好的抗载波相移能力。

图6 π/8载波偏移10 baud调制解调波Fig.6 π/8 phase shift carrier 10 baud modulation and demodulation waves
4 结束语
文中提出一种可以消除多普勒频移,而无需增加系统复杂度和时间延迟的绝对QPSK非相干解调系统。仿真实验表明该方法切实可行,完美的解决了绝对QPSK相位模糊问题,就实用性而言,此方法不仅仅可以用于卫星通信,对于同样拥有多普勒频移的地面无线通信系统也可以应用,进一步,该系统的思路还可以应用于二进制相移键控(2PSK)与大于4进制的多进制相移键控(MPSK)。
[1]BENNETT J A,DYSON P L.The effect of fairly large-scale ionospheric irregularities on satellite doppler shift original research article[J].Journal of Atmospheric and Terrestrial Physics,1982,44(4):347-358.
[2]Hibberd F H.The effect of the ionosphere on the Doppler shift of radio signals from an artificial satellite[J].Journal of Atmospheric and Terrestrial Physics,1958,12(4):338-340.
[3]You H,Garrison J L,Heckler G.Stochastic voltage model and experimental measurement of ocean-scattered GPS signal statistics[J].IEEE Trans.Geosci.Remote Sens,2004,42(10):2160-2169.
[4]黄振,陆建华,杨士中.卫星通信中多普勒频移的快速捕获[J].电子学报,2003,31(7):1052-1056.
HUANG Zhen,LU Jian-hua,YANG Shi-zhong.Rapid acquisition of doppler shift in satellite communications[J].Acta Electronica Sinica,2003,31(7):1052-1056.
[5]吕强,齐唯恐,薛永.一种新的卫星通信系统中的载波频率同步技术[J].中国空间科学技术,2012(6):75-80.
LV Qiang,QI Weikong,XUE Yong.A carrier frequency synchronization method in satellite communications system[J].Chinese Space Science and Technology,2012(6):75-80.
[6]王欣,酆广增,孔媛媛.常模盲均衡算法:消除常相位偏移和多普勒频移引起的相位模糊[J].电子与信息学报,2008,30(4):848-852.
WANG Xin,FENG Guang-zeng,KONG Yuan-yuan.Blind constant modulus algorithm:removing signal phase ambiguity generated by channel phase offset and doppler frequency shift[J].Acta Electronica Sinica,2008,30(4):848-852.
[7]甘仲民,张更新.卫星通信技术的新发展[J].通信学报,2004,27(8):2-9.
GAN Zhong-min,ZHANG Geng-xin, Current development of satellite communications technology[J].Journal on Communications,2004,27(8):2-9.
[8]王诺,戴逸民.用于卫星通信的一类UQPSK载波恢复算法及其性能的研究[J].电子学报,2004,32(7):1219-1222.
WANG Nuo,DAI Yi-min.Performance analysis of UQPSK carrieracquisition and tracking algorithm in satellite communications[J].Acta Electronica Sinica,2004,32 (7):1219-1222.
[9]赵杭生,甘仲民,屈德新.π/4-DQPSK调制的快速位同步捕获和位同步跟踪[J].电子学报,1999,27(4):24-27.
ZHAO Hang-sheng,GAN Zhong-min,QU De-xin.Symbol timing rapid acquisition and tracking forπ/4-DQPSK Signal[J].Acta Electronica Sinica,1999,27(4):24-27.
Principle of non-coherent demodulation and simulation for a new absolute QPSK
JIA Zhi-cheng1, SHI Jia-wei1, LI Yong-jun2
(1.Institute of Information Engineering, HeBei University of Technology, Tianjin 300401, China;2.National Ocean Technology Center, Tianjin 300112, China)
In order to eliminate the oscillation frequency accuracy and stability requirements of the satellite communication receiver, a new kind of absolute non-coherent demodulation for (Quadrature phase shift keying) QPSK which phase needn't recover was proposed.First, through the characteristic of four-phase waveforms we could get tow tow-rectangular waves;Second, based on the tow-rectangular waves we can get the information before modulation; At last, Estimate the ideal bit error rate.The Matlab Simulation results show that the demodulation method feasibility.Compared with conventional QPSK communication, without carrier recovery, the hardware was simple, cheap and no phase ambiguity.
satellite communication;absolute QPSK;non-coherent demodulation;code error rate;Matlab
10.14022/j.cnki.dzsjgc.2014.16.013
TN 914.3
A
1674-6236(2014)16-0041-03
2013-11-06 稿件编号:201311058
国家“863计划”资助项目(2006AA09A304)
贾志成(1957—),男,天津人,讲师,教授。研究方向:通信与电子测控。

