小开距下高速开断器稳态电弧温度场仿真研究

徐涛，李红江，杨锋

(海军工程大学电气工程学院，武汉430033)

0 引言

介质恢复特性是开关研究的重要特性之一。介质恢复性能优良则开关容易分断成功；反之，开关分断容易失败。开关能否分断成功关键在于触头间隙在介质强度恢复过程中是否能承载过电压，也就是介质强度是否恢复到一定的耐压水平，而开关间隙承受过电压的能力与开关介质恢复过程中触头间隙的热空气介质温度有关，当热空气温度高于一定值时，此时热空气会因热电离而呈现导电性，若此时加载过电压会非常易导致开关分断失败。因此开展开关的介质恢复过程瞬态温度场仿真研究是有着重大意义。而且开关电弧会直接影响介质恢复过程中触头间隙温度场，有必要开展开关电弧瞬态温度场仿真研究，而大多数电弧研究学者都是从稳态电弧特性开始研究，在分析稳态电弧特性基础上再对电弧进行瞬态电弧特性研究，因此开展稳态温度场仿真研究是有必要的。

国内外的电器研究者们在前人的理论基础上做了许多工作，建立了各种电弧模型；其中链式电弧模型和磁流体动力学模型是目前最为先进、实用的数学模型。在国外，Taczynski W[1]，Horinouchi K[2]， Meunier G[3]等人均采用链式电弧模型研究电弧的运动过程；Poeffel K[4]， Lowke J J[5]，Karetta[6]等人均是采用磁流体动力学模型、有限元法研究了整个灭弧室内气体温度场和速度场来模拟电弧的运动过程。在国内，张晋[7]等人针对低压断路器灭弧室中的磁驱电弧建立了链式电弧模型，对电弧的径向温度分布进行了计算；吴翊[8-9]等人针对低压断路器简化灭弧室建立了动态电弧的三维磁流体动力学模型，利用有限元的方法研究了整个灭弧室内的气体温度场、速度场以及气流场。而磁流体动力学模型与链式电弧模型对于研究小开距下高速开断器稳态电弧温度场太过复杂，因此根据高速开断器小开距、短燃弧的特点，建立了较为简单的单圆柱电弧模型，并利用有限差分法求解稳态电弧温度场，为以后求解高速开断器瞬态电弧温度场打下夯实的基础。

1 电弧数学模型

1.1 电弧模型及基本假定

1）电弧模型为轴对称单圆柱体，故可用二维圆柱坐标描述；

2）忽略电弧的对流散热；在触头间距小时，运用基本传热学公式推到计算，无法获得电弧的对流传热系数；

根据假定电弧模型为轴对称单圆柱体，建立高速开断器电弧模型如图1所示，将电弧模型划分为弧柱区与热边界层区，其中弧柱区呈导电导热的特性，而热边界层区只导热不导电。I为通流大小，R为电弧的半径，D为热边界层厚度，L为电弧的长度；电导率γ与热导率λ均受到温度、压力等诸多因素的综合影响，但考虑到本文的空气电弧是产生在周围均为空气的环境中，可认为电弧压力为一个标准大气压，故参数γ、λ均为温度的单值函数。

1.2 稳态电弧数学模型

1.2.1 稳态电弧数学方程

建立电弧数学模型主要是运用数学方程描述电弧某物理量满足的物理规律，如电位与温度。

对于电位，根据恒定电场中电流的连续性，则：

考虑电弧电导率随温度的变化，开断器电弧电位在柱坐标系下转化为二维场后的电位微分方程：

对于温度，考虑电弧热导率随温度的变化，故开断器温度在柱坐标系下的稳态导热微分方程为：

1.2.2 方程离散化——有限差分法

由于稳态电弧模型较为简单、规则，为了使编程容易、计算量较小，我们选用有限差分的方法进行稳态电弧数学方程的离散化。其进行数值计算的步骤如下：

1）采用一定的网格剖分方式离散化场域；根据精度与计算量的考虑，我们选取的是 0.1 mm大小的网格剖分，如图2所示。

2）电位微分方程的离散化过程如下：对于每一个网格节点均满足电位微分方程：

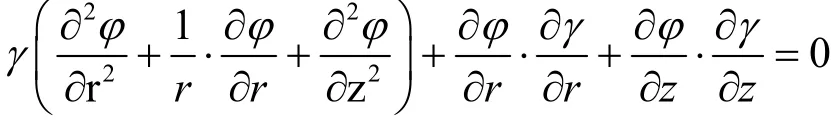
利用离散的方法将微分方程转换成线性代数方程：

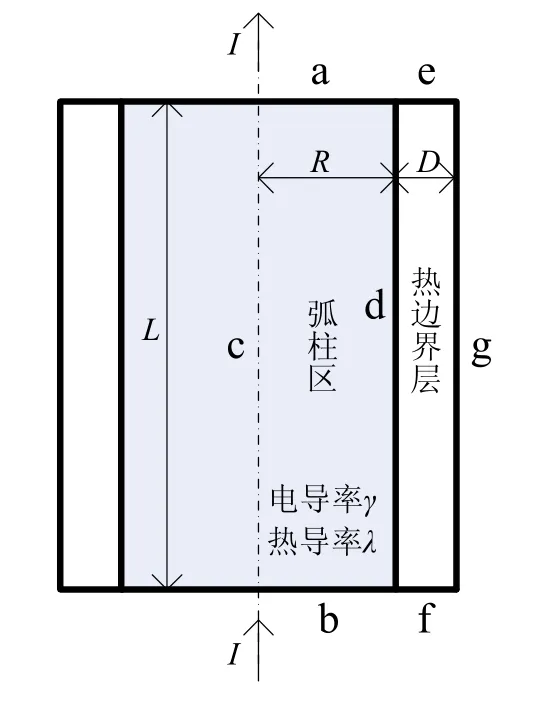
图1 高速开断器电弧模型轴截面剖分图

其中电位微分方程离散化公式为：

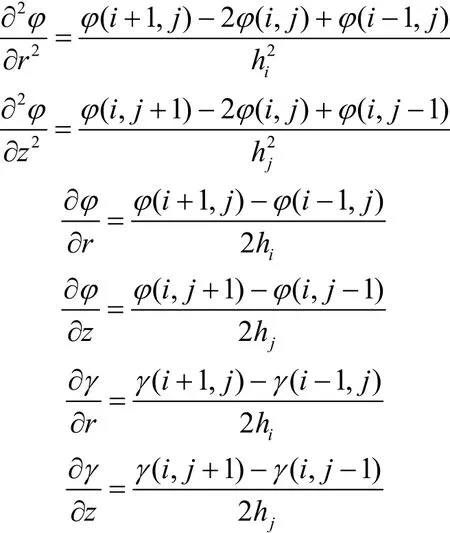
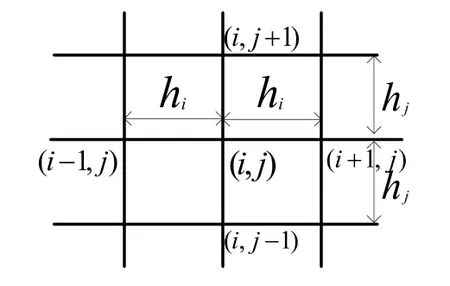
图2 网格剖分图

1.2.3 稳态电弧边界条件

1）电位边界条件

第一类边界条件：a、b边界：

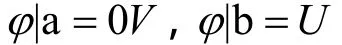
第二类边界条件：c、d边界电位变化率为0，即：

2）温度边界条件

第一类边界条件：

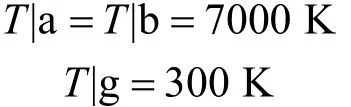
e、f边界为300 K到7000 K等差分布；

第二类边界条件： c边界绝热处理，即：

其中：γ为电弧电导率，单位为s/m，根据文献[10]可以得到电弧电导率关于温度单值函数；

λ为电弧热导率，单位为W*m-1*K-1，根据文献[10]可以得到电弧热导率关于温度单值函数；

ε为电弧净辐射系数，单位为W*m-3*sr-1，根据文献[11]可以得到电弧净辐射系数关于温度单值函数；

φ为单位体积电流源热功率，单位为W*m-3；

E为电弧电场强度，单位为V/m；

U为稳态电弧电压值；

hi、hj分别为径向、轴向的网格大小；

2 稳态电弧程序设计及仿真计算

取高速开断器电弧模型轴截面的右半边模型，计算稳态电弧电流设为直流74 A，触头间距为2 mm的稳态电弧温度场。

2.1 程序设计流程图

根据稳态电弧数学模型及设定的边界条件，对于触头间距2 mm，电弧电流74 A设计了稳态电弧温度场程序计算流程图，如图3所示。

图3 稳态电弧程序流程图

2.2 仿真计算

根据程序设计流程图，利用Matlab软件对高速开断器电弧数学模型进行编程、仿真计算，得到高速开断器电弧温度场分布情况，如图4所示，结果表示电弧弧柱中心区域温度最高， 随着电弧半径的增大温度逐渐降低，并仿真计算得到电弧半径为2.2 mm。

3 仿真结果验证

3.1 空气电弧平板实验

实验系统是由实验电路、铜丝引弧空气电弧平板实验装置、高速摄像仪、示波器及测温仪器五个部分组成的。其中空气电弧平板实验装置中两极板材料为T1铜，纯度99.95%，厚度2.98 mm，铜丝为纯铜，直径50 μm，极板开距为2 mm；高速摄像仪是每10 μs拍摄一张图片。设计了铜触头铜丝引弧空气电弧平板实验电路，如图5所示。

图4 高速开断器电弧温度场

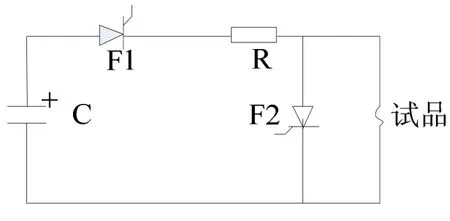
图5 空气电弧平板实验电路

该实验电路主要由电流回路与自然换流回路组成。电路参数：电路主回路电容C为50 mF，充电100 V，接R=1 Ω电阻，F1与F2均为晶闸管，试品为空气电弧平板实验装置。

3.2 实验及记录

在实验准备完毕（充电完成、示波器重置、测温光纤探头对准产生电弧处、高速摄像机对准两极板间）后，按键 S使晶闸管 F1导通，电容放电；延时600 μs，晶闸管F2导通，回路进行自然换流，直至试品中电弧熄灭；实验结束后，通过示波器得到电弧的电流和电压随时间变化的波形图，如图6所示；高速摄像机记录一组铜丝引弧空气电弧平板实验从起弧到熄弧的高速摄像图片，如图7所示。

3.3 实验数据处理

1）读取电弧稳定燃弧时刻的电流及电压

由于高速摄像仪是每10 μs拍摄一帧，则对应每一张空气电弧图片的电流电压只需在实验示波器得出的电流电压实验波形中读出，将示波器所得空气电弧电流电压实验波形导入 Matlab软件中，在Matlab软件中直接读取每一帧的电流电压，则电弧稳定燃烧时刻的电弧电流、电压分别为74 A、30 V。

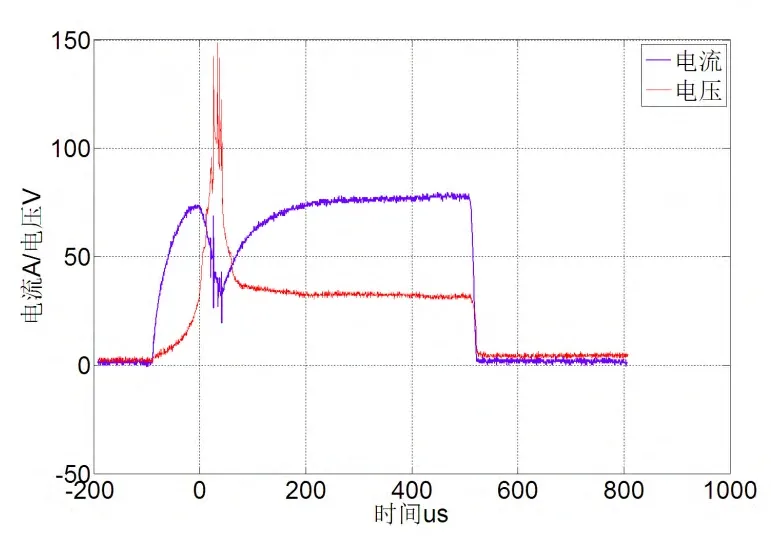
图6 电弧的电流和电压实验波形

图7 空气电弧平板实验高速摄像

2）稳态电弧直径及热边界层直径的量取

取高速摄像仪记录的空气电弧稳定燃弧时的一张图片，将其导入Autocad软件中，标注两极板间的长度、电弧长度及电弧直径分别得到三个数据，如图8所示，其中认为图中最亮部分的宽度为电弧直径、电弧周围稍安的部分为电弧热边界层，则图中10.14为两极板间长度与电弧长度、21.26为电弧直径，又由于两极板间的实际距离为 2 mm，则可计算得到电弧长度的实际值为 2 mm。

同理还可计算得到稳态电弧直径实际值分别为4.6 mm。

通过比对相同电流下仿真计算出的稳态电弧半径2.3 mm与实验测量出来的电弧半径2.3 mm，基本可以论证稳态电弧仿真基本合理，仿真结果较为准确。

图8 Autocad中标注电弧各尺寸的图片

对于不同触头开距、不同电流大小，开展了大量的稳态电弧温度场仿真计算与实验验证，得到如下的结果：

?

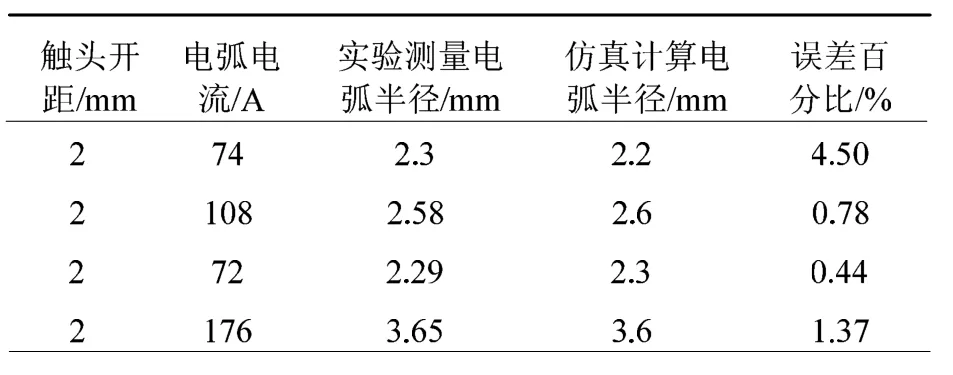
4 结论

本文仿真计算了高速开断器稳态电弧温度场和稳态电弧电流下的电弧半径。利用有限差分法对高速开断器稳态电弧温度场进行数学建模，具体讨论了仿真模型中各方程所需的边界条件， 利用Matlab软件进行编程、仿真计算，并与空气电弧平板实验中测量的稳态电弧半径进行比对，误差在工程科允许范围内，基本可以论证稳态电弧温度场仿真结果基本准确。这为以后研究高速开断器瞬态电弧温度场打下夯实基础。

[1]Tarczynski W, Bolanowski B, Hejman T. Simulation of arc motion in rail electrode systems[A]. Proc 7th Int Conf on Switching Arc Phenomena[C]. Lodz:Poland, 1993: 58-63

[2]Horinouchi K, Nakayama Y, Kohyama H, et al.Practical simulation method for magnetically driven arc in a gas[A]. Proc 11th Int Conf on Gas Discharges and Their Applications[C]. Tokyo: Japan, 1995:102-195

[3]Meunier G, Abri A. Simulation of the arc interruption in circuit breaker[A]. Proc 5th Int Conf on Switching Arc Phenomena[C]. Lodz: Poland, 1985: 105-109

[4]Poeffel K. Influence of the copper electrode surface on initial arc movement[J]. IEEE Trans on PS, 1980,8(4): 443-448

[5]Lowke J J, Kovitya P, Schmidt H P. Theory of free-burning arc columns including the influence of the cathode [J]. J Phys D:Appl Phys, 1992, 25:1600-1606

[6]Karetta F, Lindmayer M. Simulation of the gasdynamic and electromagnetic processes in low voltage switching arcs[J]. IEEE Trans Compon Package Maunf Technol, 1998, 21(1): 96-103.

[7]张晋, 陈德桂, 付军. 低压断路器灭弧室中磁驱电弧的数学模型[J]. 中国电机工程学报, 1999, 19 (10):22-26.

[8]吴翊, 荣命哲, 杨茜, 胡光霞. 低压空气电弧动态特性仿真及分析[J].中国电机工程学报, 2005,25(21): 143-148.

[9]吴翊, 荣命哲, 王小华, 孙志强, 李剑. 触头打开过程中低压空气电弧等离子体的动态分析[J].电工技术学报, 2008,23(5):12-17.

[10]吴翊. 低压空气电弧多场耦合过程的仿真及实验研究[D]. 西安: 西安交通大学, 2006.

[11]Vladimir Aubrecht, Milada Bartlova. Net Emission Coefficients of Radiation in Air and SF6 Thermal Plasmas[J]. Plasma Chem Plasma Process 2009, 29:131–147.