异步电机磁链观测技术的研究

张礼运，张亚东，康乐

(1. 中海油田服务股份有限公司，北京101149；2. 武汉船用电力推进装置研究所，武汉430064)

0 引言

异步电机运行时电机实际磁场很难通过直接的手段观测出来，通常采用间接手段观测异步电机在各种工况下的磁场。但实际电机为非线性系统，存在磁场饱和、磁场交叉影响、参数摄动等因数的影响，这导致基于理想电机的磁链观测模型观测的磁链与电机实际磁链在幅值和相位上存在偏差，直接影响异步电机铁磁材料的利用率（在磁饱和拐点充分利用铁磁材料），降低了异步电机矢量控制的解耦特性，降低了异步电机的动态性能，严重时导致电机无法正常工作。因此，必须采取措施提高异步电机的磁场观测精度和鲁棒性，保证异步电机在任何工况下，观测磁链与实际磁链在幅值和旋转角度上基本保持一致。

目前控制系统中磁链观测模型采取在理想电机数学模型基础上建模，通过可测量来校正、补偿观测的磁链，提高磁链观测的鲁棒性、精度[1]。

本文基于异步电机矢量控制系统的磁链观测进行研究与探索。

1 基于异步电机模型下的磁链观测

1.1 电流模型

磁链观测的方法很多，最基本的是从电机理想模型出发得到的电流模型、电压模型、以及两者结合的观测方法。

根据异步电机数学模型得到：

电机存在磁饱和特性和磁场交叉耦合，同时转子电阻也随转子温度的上升而变化，这限制了电流模型仅能用于低速工况下，且观测转子磁链幅值和旋转角度与电机实际转子磁链幅值和旋转角度有一定的差别。同时定子电流的采样误差、控制用的电机参数的误差也会造成观测转子磁链幅值与电机实际转子磁链幅值有一定的差别，这些严重影响了控制系统性能。

1.2 电压模型及改进方法

省去繁琐推导，得到电机电压模型为：

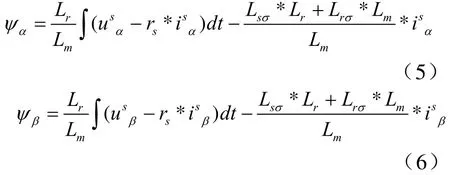
由于电压模型中用到了积分环节，带来积分漂移和积分累积误差影响实际系统性能。因此需要对电压模型积分环节作一定处理。

在实际应用中为了减小积分器的直流漂移，抑制低频噪声，对积分器进行了改进，常用的解决方案有低通滤波器、磁链补偿等几类。

尽管采用串联低通滤波器能减小漂移，但低通滤波器的时间常数，实际中n一般不会很大，这导致低通滤波带来的幅值和相位误差仍然很大。如果滤波器的时间常数是固定值，电机频率比滤波器频率低时会产生磁链估算误差，可编程的滤波器方法使滤波器时间常数随同步旋转频率的升高而变小，滤波器的极点在非常低的速度范围内接近原点，在高速范围内远离原点，从而减小低速时磁链观测误差，但是过大的时间常数会导致直流偏置[2]，所以低通滤波方法存在幅值和相位误差，故一般采取低通滤波器和一阶高阶滤波器的结合，对低通滤波器带来的幅值和相位误差进行补偿。这种积分器磁链估计的精度主要依靠限幅的取值。当限幅取值与磁链值相等时，效果是最好的。若电机在磁链幅值变化（如弱磁模式）情况下运行时，积分器限幅取值也要作相应的调整，这会给实际操作带来不便。另外由于本方法只是对磁链幅值做了补偿处理，在磁链计算的相位误差上没有能很好的改善，导致在带载接近满载的时候由于磁场观测不准而出现过流跳闸。

1.3 电压、电流混合模型方法

为了解决电压模型、电流模型在全速范围内的估计精度问题，可以综合两种模型的特点，结合起来使用，在高速时，采用低通滤波器滤除电流模型估计值，在低速时，采用高通滤波器滤除电压模型估计值，为了实现二者平滑切换，可令高通、低通滤波器二者转折频率相等[3]。

原理如下：

电压模型计算结果输出转子磁链分量

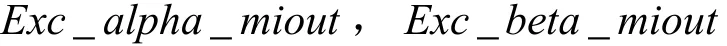
电流模型计算结果输出转子磁链分量

则输出转子磁链计算

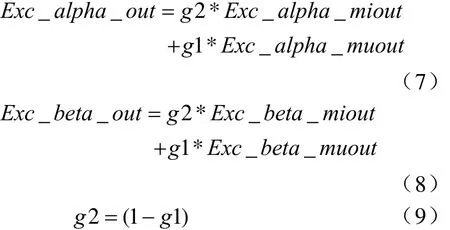
其中g1的确定如图1所示：

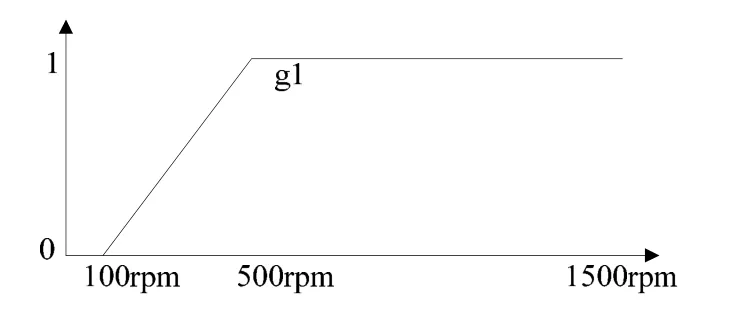
图1 切换因子g1

计算得到转子磁链分量后，由Exc_alpha_out，Exc_beta_ out计算转子磁链角度的正弦余弦值Sin_fys_mu与Cos_fys_mu，其中混合模型共同作用段为100～500 rpm，切换过程比较平稳，如果混合模型段太短（例如100～150 rpm）容易导致切换时候电流变大，严重时导致过流保护。

2 磁链闭环观测

为了增强磁链观测对干扰的抑制能力需要引入各种闭环反馈措施，以增强观测器的稳定性，并提高状态估计精度；常见的两种反馈结构是输出反馈和状态反馈，为了实现转子磁链闭环观测模型，必须以实际电机模型为参考模型，以磁链观测模型为可调模型，当观测模型与实际某些量发生偏差时（这些量必须是状态误差存在时，该误差就不为0），通过将误差引入反馈中，最终使二者状态误差为0。如图2所示[5]。

常用的闭环反馈措施有：龙贝格磁链观测器、基于Kalman滤波的磁链观测器。异步电机龙贝格磁链观测器可在不同坐标系下实现磁链观测；根据异步电机数学模型和龙贝格观测理论，通过引入状态误差反馈，可设计转子磁链观测器，一般采取定子电流和转子磁链作为状态变量（状态反馈），也有采取定、转子磁链作为状态变量的（输出状态反馈）。Kalman滤波采用白噪声为随机干扰信号和测量噪声信号建模，必须事先知道误差和测量噪声的统计特性，实际系统中只能反复仿真和试验来选择合适的参数,比较难以在工程实践中推广运用。现对采取定子电流和转子磁链作为状态变量的龙贝格磁链观测器进行分析。

三相异步电机在旋转坐标系下的磁链和电压方程分别为[4]：

省去中间过程推导，在进行状态反馈时由于实际中转子磁链很难观测到，所以仅采用实际电机定子电流与估算的定子电流差作为状态反馈量，同时观测定子电流、转子磁链的全阶磁链状态观测器（输出反馈），可以用下面公式描述[5]：

通过极点配置的方法得到增益矩阵：

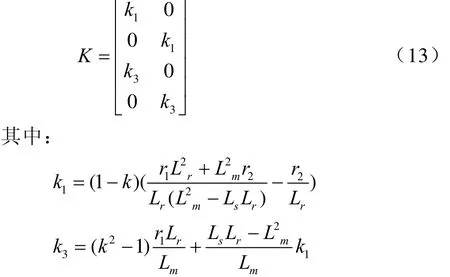
应用中可根据控制精度适当选择离散算法，离散算法越精确，控制效果越好，但过于复杂的离散算发对硬件资源要求极高。

图2 状态观测器及其实现状态反馈图

在龙贝格转子磁链观测模型中，采样误差和干扰模型通过电流误差校正环节输入到系统中去，这很大程度上提高了系统的抗干扰能力；为保证观测器的稳定性，其反馈矩阵参数一般通过极点配置方法选取，如果极点离虚轴太近，则观测器的收敛速度太慢，若极点离虚轴太远，观测器对测量噪声的抑制作用减弱，因此，需要凭经验不断调整反馈增益矩阵，以保证观测器在任何频率下都稳定，同时收敛速度也满足要求。

图3 磁链轨迹

3 实验结果及结论

采用数字离散法，对200 kW异步电机进行实验验证：当电机转速达到800 rpm/m，电机输出功率为83 kW时观测到的相关波形如图4。

本文对异步电机的磁链观测技术进行了论述，首先对磁环开环电流、电压及混合观测的数学模型进行分析，然后对闭环磁链进行较全面论述，重点对龙贝格转子磁链观测模型进行理论分析，并通过实验验证了该方法的工程使用价值。

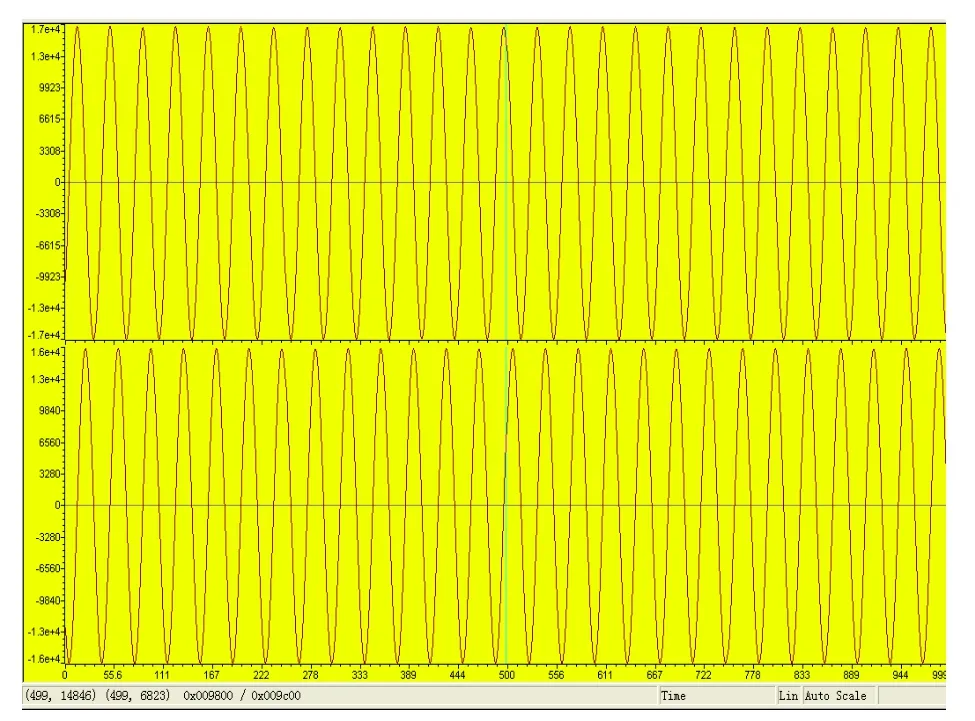
图4 转子磁链α轴与β轴分量

[4]C. G. Hodge, D. J. Mattick. The electric warship[J].Transaction on International Marine Engineering, 108,part2, 1996: 109-125.

[5]刘忠举, 刘梁宝明等. 基于改进型积分器的矢量控制系统研究. 电力电子技术, 2010, 2: 12-17.

[6]翁海清, 李发海, 刘丛伟. 异步电机降阶磁链观测器的研究. 清华大学学报, 2001, 41: 9.

[7]辜承林, 陈乔夫. 电机学. 武汉: 华中科技大学出版社, 2001.

[8]陈坚. 交流电机数学模型及调速系统. 北京: 国防工业出版社, 1989.