基于单轴速率转台的角速度传感器标定方法*

赵新强, 晁代宏, 宋来亮

(北京航空航天大学 仪器科学与光电工程学院，北京 100191)

0 引 言

光纤陀螺是光纤捷联惯导系统的主要部件，是基于Sagnac效应发展起来的一种光电式惯性传感器，作为角速度传感器，它无需机电陀螺所必需的高速转子，在性能方面的优势相当明显，具有高灵敏度、高精度、高可靠性、大动态范围、对加速度和振动不敏感、结构紧凑等优点，是新一代捷联惯导系统的理想传感器，因此，近些年来光纤陀螺广泛应用于惯性导航领域[1～3]。3只以正交形式安装的光纤陀螺组合作为惯导系统的主要部件广泛应用于姿态的测量与控制领域。

为提高惯导系统的使用精度，通常需要对其标定。标定技术就是一种从软件方面来提高惯导系统实际使用精度的方法,其本质上也是一种误差补偿技术。所谓误差补偿技术就是建立惯性器件和惯导系统的误差数学模型，通过一定的试验来确定模型系数，进而通过软件算法来消除误差[4～6]。标定技术一直是国内外相关行业的研究热点,为挖掘惯导系统精度潜力，国内外对标定技术进行了大量、深入的研究工作。惯导系统标定是惯性导航的前提，标定结果的好坏对惯性导航精度会产生直接的影响[7]。在仪表硬件条件不变的情况下，经过误差补偿后的系统精度会有显著提高。定期对惯导系统进行标定测试，并修正惯性器件测量误差，是提高惯导系统导航精度的有效手段[8]。

传统的惯性器件实验室标定方法一般使用双轴或三轴位置速率转台，对设备要求高，操作较复杂而且需要精确的北向基准[9]。

本文提出一种基于单轴速率转台的光纤陀螺捷联航姿系统的快速标定方法，很好地解决了传统标定方法的一些问题，且满足一定的标定精度要求。

1 光纤陀螺捷联航姿系统的构成

光纤陀螺捷联航姿系统主要由惯性测量组件与倾角仪构成，其中3只光纤陀螺正交配置构成惯性测量组件，用于测量载体的角速度，并通过姿态解算实时求得载体的姿态角。由于惯性系统的误差是随时间积累发散的，所以,航姿系统中采用倾角仪实时修正由惯性测量组件测得的水平姿态角(俯仰角与横滚角)。

3只光纤陀螺以正交配置方式构成惯性测量组件，其3个角速度敏感轴x,y,z符合右手定则，如图1所示。

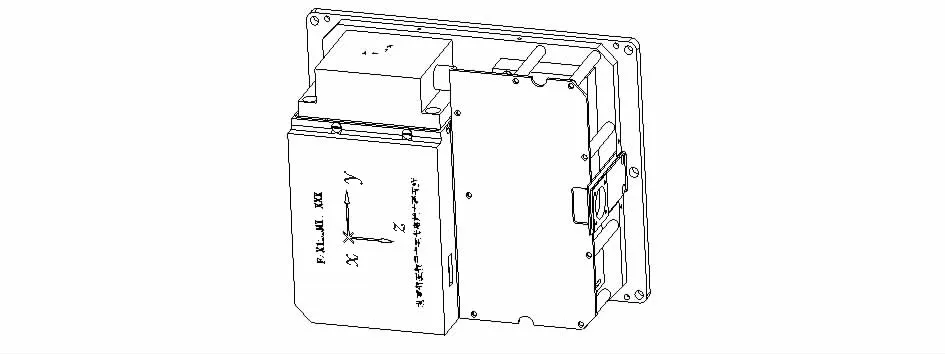
图1 系统结构图

2 光纤陀螺捷联航姿系统的误差模型

理想情况下，航姿系统中3个光纤陀螺敏感轴相互间正交，但由于实际安装原因，3个光纤陀螺敏感轴不能达到理想正交，因此,需要得到光纤陀螺敏感轴与正交坐标系的关系，实现正交化要求，通过失准角建立3个光纤陀螺敏感轴与正交坐标系的关系，如图2所示。航姿系统是由3只光纤陀螺组成，单个光纤陀螺误差也是标定的对象，仪表输出与测量的真实值有比例关系，称为标度因数，当测量的真实值为零时，仪表输出不为零，称为零偏。通过对3只光纤陀螺的误差特性进行分析，需要标定的参数主要包括失准角、标度因数误差以及零偏。

光纤陀螺标度因数记为kgx,kgy,kgz，失准角记为Egxy,Egxz,Egyx,Egyz,Egzx,Egzy，零偏记为Bgx,Bgy,Bgz，光纤陀螺感知到的标准输入角速度记为ωx,ωy,ωz，光纤陀螺的输出记为Fgx,Fgy,Fgz，航姿系统的误差模型如下所示

(1)

其中,kgxEgxy,kgxEgxz,kgyEgyx,kgyEgyz,kgzEgzx,kgzEgzy可分别表示为kgxy,kgxz,kgyx,kgyz,kgzx,kgzy。

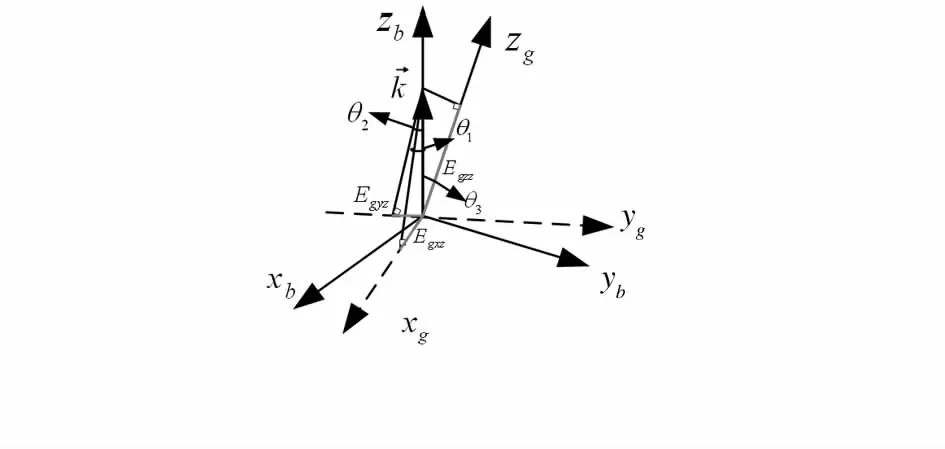
图2 失准角示意图

3 标定方法

标定的实质即为失准角、标度因数、零偏的获取，将惯性器件的测量数据用标定参数进行补偿后再进行导航解算从而提高导航精度。

首先，通过工装将光纤陀螺捷联航姿系统安装于单轴速率转台的台面上，使z轴陀螺的敏感轴垂直于转台台面，x轴与y轴陀螺敏感轴朝向任意方向，如图3所示。

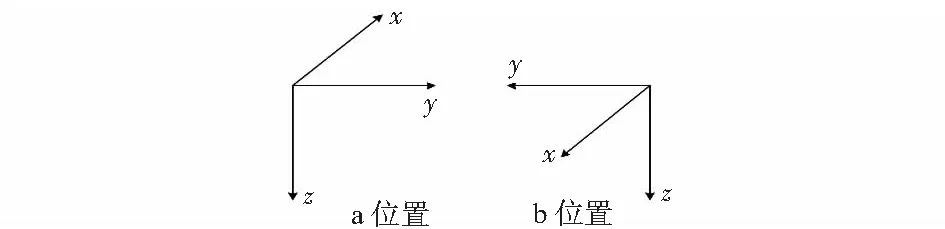
图3 第一次安装示意图

然后，静态采集陀螺数据。在图3中a位置进行一次静态采集，然后控制单轴速率转台旋转180°转到b位置进行相同时间的静态采集。

最后，控制单轴速率转台按一定速率正转n周，采集陀螺的数据，并控制单轴速率转台按相同速率反转n周采集陀螺数据。

如图4与图5所示，使y轴陀螺与x轴陀螺分别朝下按照同样的步骤控制单轴速率转台，采集陀螺数据。

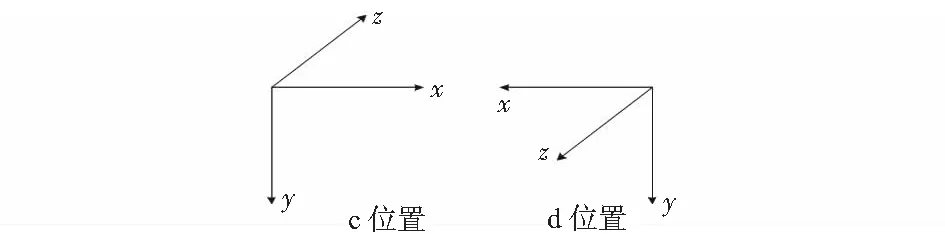
图4 第二次安装示意图

图5 第三次安装示意图

3.1 标度因数与失准角的标定

在图3中设正转的转速为ω，L为地理纬度，ωx,ωy,ωz分别为光纤陀螺组件理想正交坐标系x轴、y轴、z轴的角速度，则光纤陀螺的标准输入角速度为

(2)

将式(2)带入式(1)得

(3)

(4)

(5)

其中，Figj中的i=1,2,3，代表第i次将系统安装于单轴速率转台台面上；j=x,y,z，代表本轴向光纤陀螺。

假设N为采集到的数据个数，将陀螺所有数据求和得

(6)

同样控制单轴速率转台以-ω反转n轴，将陀螺所有数据求和得

(7)

将式(7)与式(6)作差可得

(8)

(9)

(10)

在图4中，y轴垂直于单轴速率转台的台面，同理可得

(11)

(12)

(13)

在图5中，x轴垂直于单轴速率转台的台面，同理可得

(14)

(15)

(16)

由公式(8)～式(16)联立可得光纤陀螺的标度因数和安装失准角

3.2 零偏的标定

利用上述6个位置静态采集的处于水平方向光纤陀螺的数据求取零偏，可以消除地球转速对标定的影响。

如图3～图5所示，设静态下采集到的光纤陀螺的数据平均值表示为Nij，i=1,2,3,5,6，代表第i个位置；j=x,y,z，代表本轴向光纤陀螺,则可得光纤陀螺的零偏

4 转台误差对标定精度影响的讨论

转台的位置精度对标定会有一定的影响，转台位置精度对陀螺标度因数和安装误差的标定精度的影响为d/2nπ(d为转台位置精度)，一般转台的位置误差在角分以内，对于光纤陀螺而言，转台位置精度引起的标定误差可忽略。转台在转动过程中，可能存在转速不均匀的情况，此时，地球的角速度在水平上的分量在标定过程中不能完全消除，对标定结果产生一定的影响，但对一般的转台来说，该影响较小，可以忽略[10]。

5 试验验证

采用实验室某光纤陀螺捷联航姿系统进行本标定方法的试验验证，陀螺精度为0.1°/h。

利用单轴速率转台对光纤陀螺捷联航姿系统按照本标定方法进行标定，每次静态采集时间为5 min，转台以2°/s,10°/s,30°/s,60°/s,100°/s共5个速率做正反转试验，每次转动时间为3 min，标度因数与失准角取5个速率下的平均值，标定结果如表1所示，其中,标度因数单位为pulse/((°)/s ·10 ms)，失准角单位为rad，零偏单位为pulse/10 ms，系统数据采集周期为10 ms。

为了验证标定结果的可靠性，在姿态解算程序中用标定参数对陀螺数据进行补偿。将光纤陀螺捷联航姿系统安装于3轴转台上,并依次控制转台3个轴摇摆进行三轴摇摆试验测量姿态角，时间为1 h，摆幅10°，摆动周期5 s，摆动频率0.2 Hz，姿态测量1 h后控制转台复位到测量开始时转台的位置，将姿态测量数据保存，并用数据分析软件进行分析，姿态测量结果如图6所示。

表1 标定结果

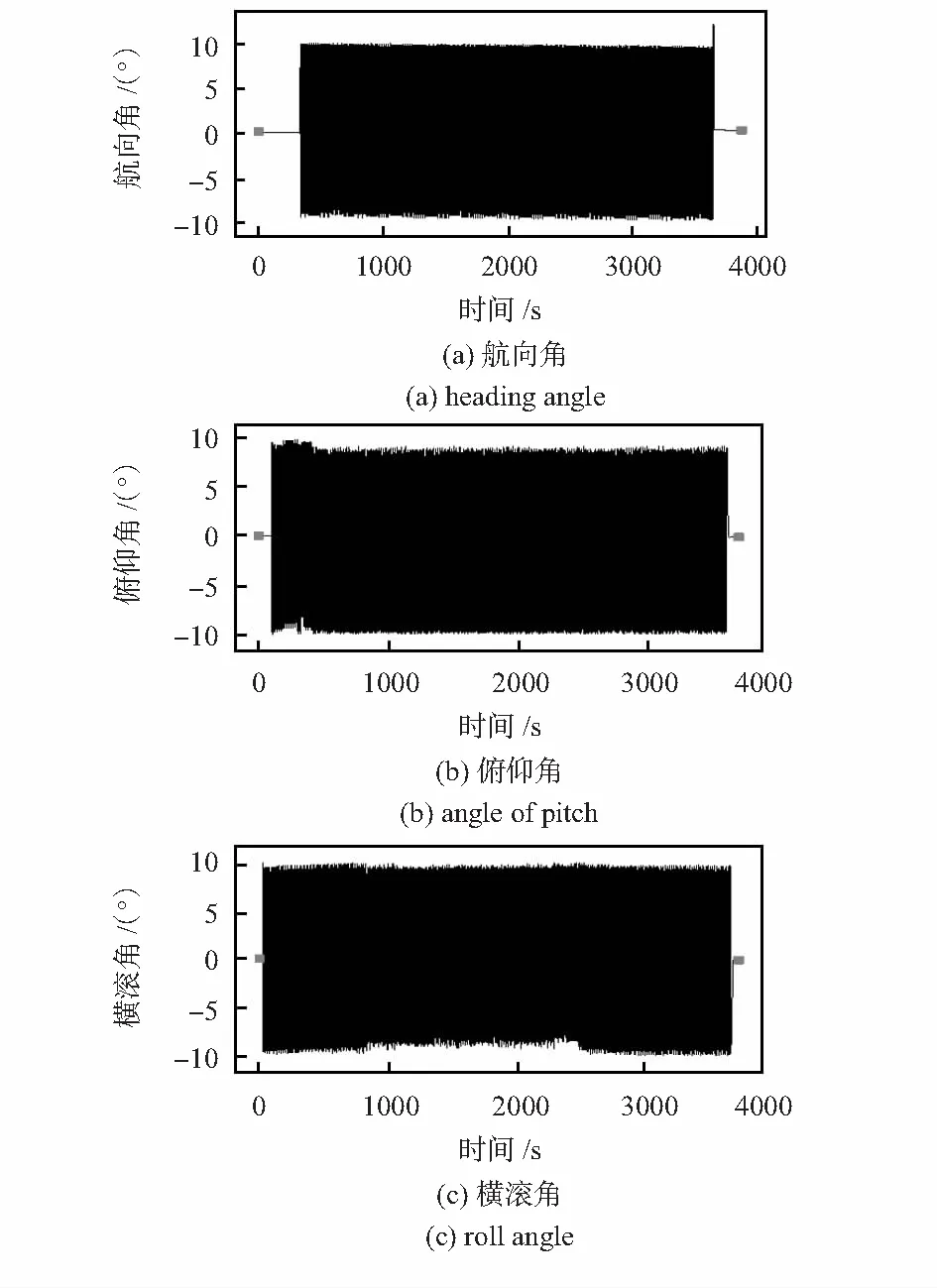
图6 姿态图

姿态角测量误差如表2所示。

本系统采用的光纤陀螺的精度为0.1°/h，从对系统的姿态进行的1 h测量结果来看，标定精度达到了预期的要求。

6 结 论

本文分析了构成捷联航姿系统的光纤陀螺组件的误差补偿模型，提出了基于单轴速率转台的标定方法，并进行了试验验证，验证结果表明：该方法能够保证光纤陀螺组件的误差参数标定精度。该方法只需单轴速率转台作为标定设备，成本低且不需要北向基准，是一种适合于中低精度光纤陀螺捷联航姿系统的快速标定方法，具有一定的工程应用价值。

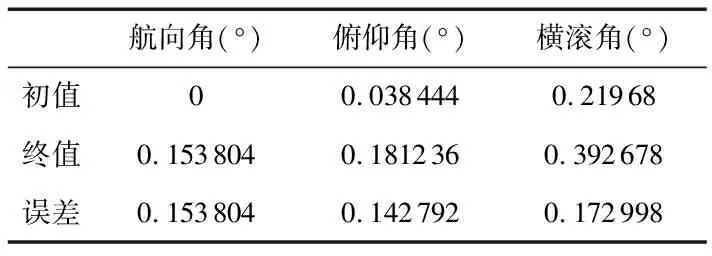
表2 测量误差

参考文献:

[1]陈 哲.捷联惯性导航系统原理[M].北京:宇航出版社，1986.

[2]丁 枫.基于双轴转台的光学捷联惯导标定方法研究[D].北京：北京航空航天大学，2012.

[3]肖桂平.光学陀螺捷联惯导系统的标定精度分析[D].长沙：国防科技大学，2008.

[4]Heckman D W,Baretela M.Interferometric fiber optic gyro technology(IFOG)[J].IEEE Aerospace and Electronic Systems Magazine,2000,15(2):23-28.

[5]Goad C.Precise positioning with the global positioning system[C]∥Proc of the 3rd International Symposium on Inertial Technology for Surveying and Geodesy,Banff,Canada,1986:745-756.

[6]Zhang Hongliang,Wu Yuanxin,Wu Wenqi,et al.Improved multi-position calibration for inertial measurement units[J].Measurement Science and Technology,2010，21(1):1-11.

[7]顾东晴，秦永元，严恭敏,等.基于多元回归模型的捷联惯性测量组件标定技术[J].测控技术，2005,24(3):59-61.

[8]以光衢.惯性导航原理[M].北京：航空工业出版社，1987.

[9]党建军，罗建军，万彦辉.基于单轴速率转台的捷联惯测组合标定方法[J].航空学报，2010,31(4):807-811.

[10] 张树侠，闫 威.激光陀螺捷联系统安装误差的标定[J].中国惯性技术学报，2000,8(1)：47-49.