基于BP神经网络的含CO2天然气偏差因子预测

陈亮，袁恩来，孙雷

（1.中国石油新疆油田公司勘探开发研究院，新疆 克拉玛依 834000；2.中国石油新疆油田公司实验检测研究院，新疆 克拉玛依 834000；3.西南石油大学油气藏地质及开发工程国家重点实验室，四川 成都 610500）

0 引言

CO2摩尔分数对天然气偏差因子有较大的影响。CO2作为酸性气体，对天然气临界参数的影响不可忽视，至今尚无准确求取含CO2天然气体系临界参数的简单方法，常规计算主要是对拟临界参数进行校正。当天然气中含非烃气体（CO2，H2S，N2）和水蒸气时，其临界参数校正方法主要有以下3种：1）考虑CO2，H2S及N2影响的 Car-Kobayshi-Burrows 方法［1］；2）考虑 H2S，CO2影响的 Wichert-Aziz 校正方法［2］；3）郭绪强校正法［3］。研究表明［4-9］，各种校正方法仅适用于非烃气体摩尔分数较低的情况，CO2摩尔分数越高，误差越大，经验公式及临界参数校正方法则表现出较强的不适应性。

神经网络系统具有强大的自组织、自学习、自适应能力，可对未知体系进行科学学习及合理预测［10-13］。笔者以BP神经网络为基础，以实验压力（p）、实验温度（T）、修正前体系临界参数（ppc，Tpc）及 CO2摩尔分数作为输入变量，绕过直接准确求取含CO2天然气混合体系临界参数的过程，对含CO2天然气偏差因子进行预测，同时与常规经验模型进行对比，评价含CO2天然气偏差因子计算模型的适应性。

1 BP神经网络建立

BP神经网络是一种人工智能模式识别方法，具有高度并行的处理机制、高度灵活可变的拓扑结构以及强大的预测分析能力［10］，目前已广泛应用于科学研究预测。

1.1 模型建立

BP神经网络可以包含1层或多层隐含层，在不限制其隐含层节点数的情况下，具有通过1层隐含层就可实现任意非线性映射的功能，其模型结构包括输入层、隐含层和输出层。如何确定有代表性的输入参数，是模型预测的关键。

含CO2天然气偏差因子预测，其输入层代表的是含CO2天然气的主要特性，通过这个主要特性来进行神经网络的学习，根据学习到的结果计算其他任意CO2摩尔分数天然气的偏差因子。范德华对应状态原理说明，一种物质的物理参数是它对应临界点物性参数的函数［14］。偏差因子亦然，可表示为

式中：pr为对比压力；Tr为对比温度；p为气体的绝对压力；T为气体的绝对温度。

式（1）表明，偏差因子主要由体系的 T，p，Tpc，ppc决定。根据文献［1-3］，前述3种校正方法修正后的酸性气体临界参数均是天然气中非烃气体（CO2，H2S，N2）摩尔分数及修正前体系临界参数（ppc，Tpc）的函数。

综合分析，本模型输入层参数选择实验压力（p）、实验温度（T）、修正前体系临界参数（ppc，Tpc）及 CO2摩尔分数作为输入变量进行预测，因此，输入层节点数为5，输出为偏差因子，输出层节点数为1。根据计算要求，本模型选用1层隐含层的神经网络结构，神经元个数为5。采用MATLAB神经网络工具箱提供的神经网络专用函数newff（）进行计算。

1.2 训练及学习方法选择

网络训练与学习就是通过调整权重和阀值，使网络的输入和输出反复作用于初始化的网络，以使网络误差最小，从而实现输入输出间的非线性映射。

神经网络有多种训练和学习方法，本模型以批变模式来训练网络函数，设置训练的目标均方差为0.001，学习速率为0.05。

1.3 模型验证

本模型选用相对误差来反映预测数据偏离实验测定值的程度。学习样本数据主要来自文献［4-7］，总计249个学习样本。CO2摩尔分数分布如表1所示，所选样品均具有较强的代表性。

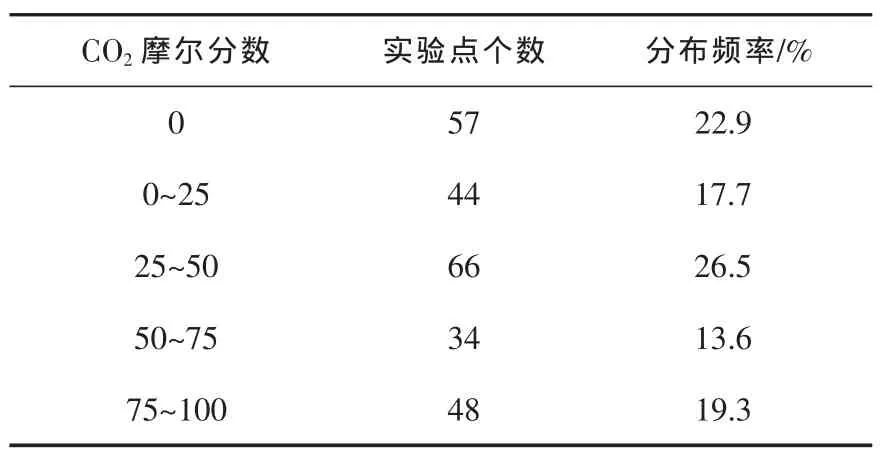
表1 CO2摩尔分数分布

BP神经网络预测值与实验值对比结果见图1。从图1可以看出，预测值与实验值正好分布在45°线上，这表明通过一定训练后，预测值与实验值吻合较好。

图1 偏差因子BP神经网络预测值与实验值对比

定义相对误差为

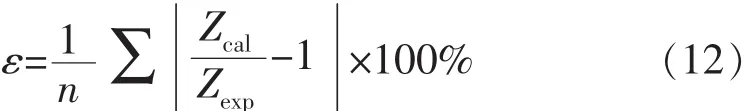
式中：ε为相对误差，%；Zcal为BP神经网络预测偏差因子；Zexp为实验测定偏差因子；n为学习样本点数。

根据相对误差计算公式，模型验证数据的相对误差仅为0.76%，预测精度很高。

2 模型应用

为验证模型的有效性，采用DBR-PVT仪测定了不同CO2摩尔分数天然气的偏差因子，所选气体CO2摩尔分数分别为 0%，23.60%，53.31%，87.32%，98.67%，样品组分见表2。实验温度80℃，实验压力0.10～42.34 MPa。实验测试按照《天然气藏流体物性分析方法》进行，结果见图2。

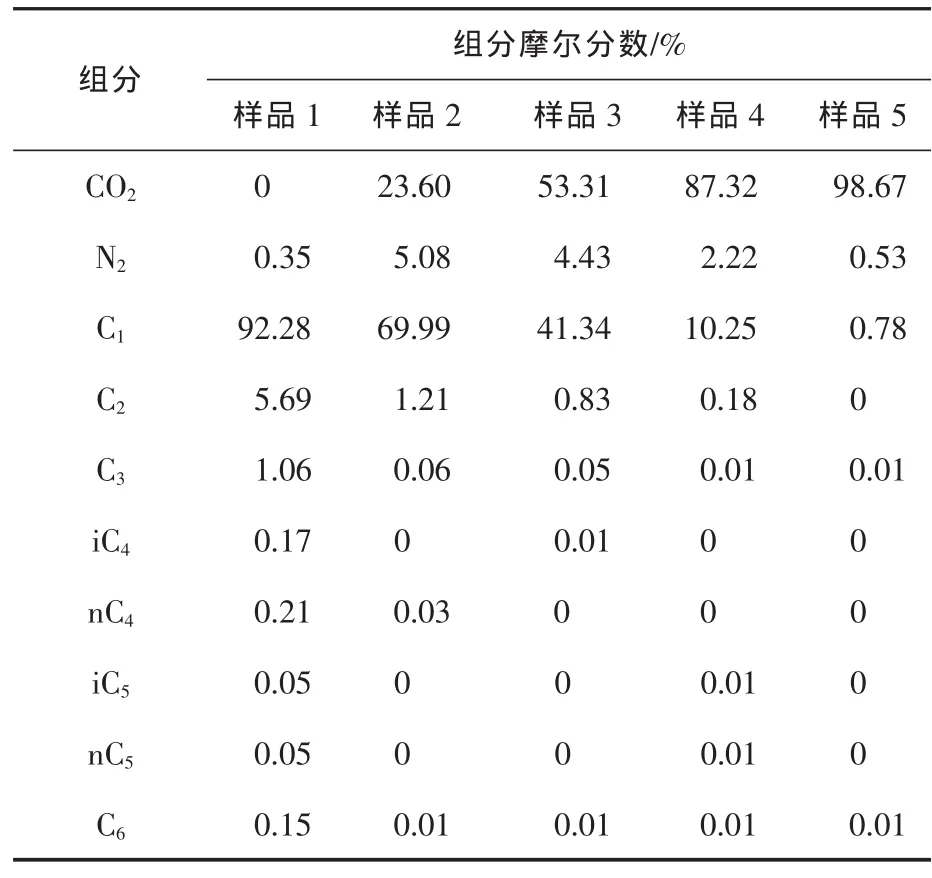
表2 测试样品组分

图2 不同CO2摩尔分数下天然气偏差因子实测数据

从图2可以看出，CO2摩尔分数对天然气偏差因子有较大的影响。CO2摩尔分数越高，天然气偏差因子越小。这说明，天然气中CO2摩尔分数越高，相同状态下气体偏离理想气体的程度越大。

根据实验数据，以 p，T，ppc，Tpc及 CO2摩尔分数作为输入变量，对其进行预测，预测结果见图3。

图3 偏差因子实验值与预测值对比

从图3可以看出，预测值与实验值正好分布在45°线上，表明预测值与实测值吻合程度较高。

3 偏差因子模型计算对比

为了评价BP神经网络对含CO2天然气偏差因子计算的适用性，将BP神经网络预测结果与经验公式计算结果进行对比。综合考虑混合规则（Key′s，SBV和RK）和校正方法（CKB，WA及GXQ），选取了目前常见的经验公式（DAK，DPR，HY，Papay，BB，Granmer、张国东及李相方模型）［15-20］，总计48种组合，对5组实验进行综合评价。计算结果表明，经验公式（DPR，HY，BB）+修正规则（Key′，RK）+校正方法（WA，GXQ）组合计算含CO2天然气偏差因子效果最好，相对误差见表3。

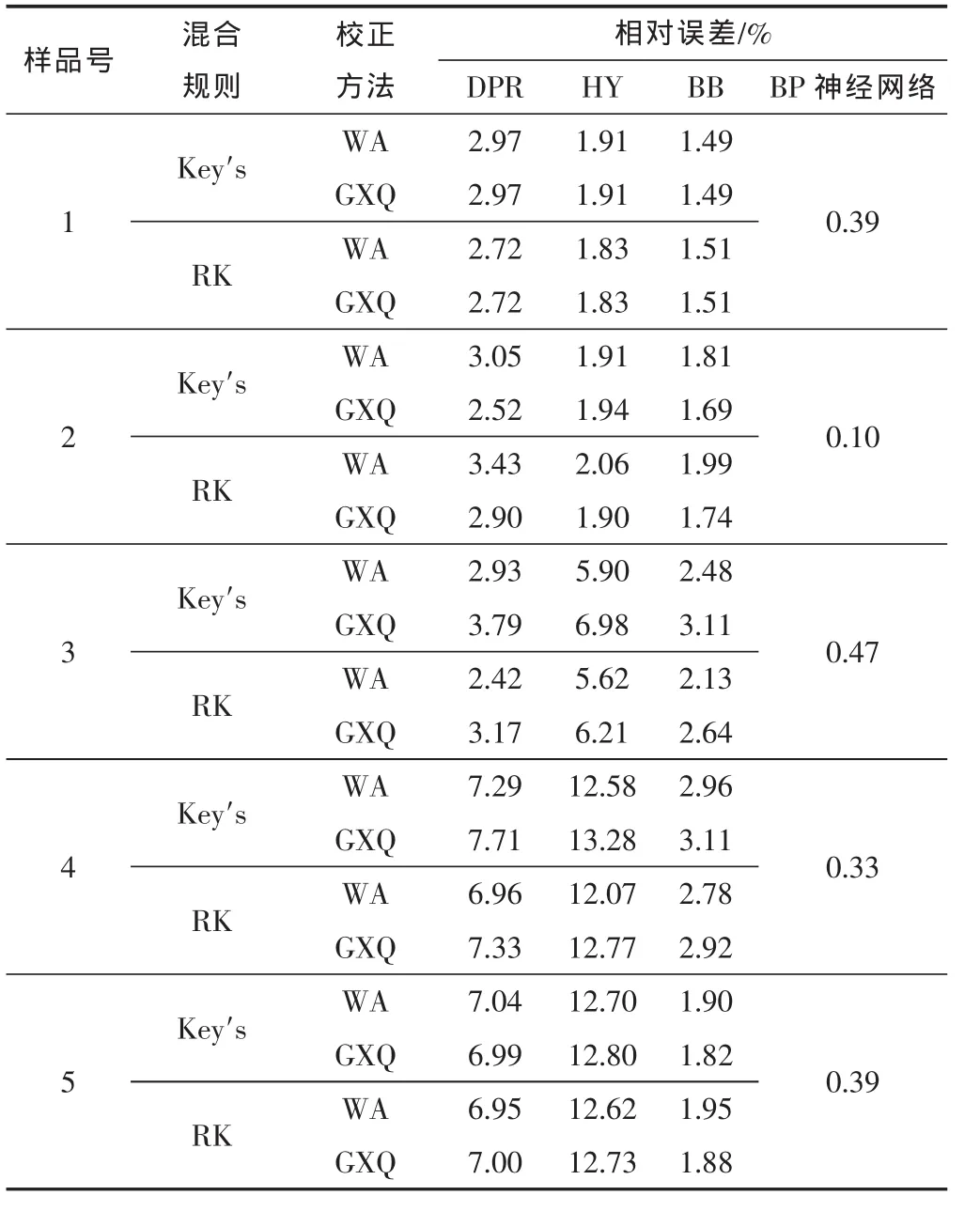
表3 不同方法计算CO2气藏气体偏差因子误差对比

由表3可知：1）常规偏差因子计算模型中，BB模型计算CO2气藏气体偏差因子的精度较高；2）对于CO2摩尔分数低于50%的天然气（如样品1、样品2），HY，DPR及BB方法计算的精度都较高，误差小于3%；当CO2摩尔分数超过50%时（如样品3、样品4及样品5），DPR及HY方法表现出较强的不适应性，计算误差大于5%，不能满足工程要求，BB法适应性较强，误差均小于5%；3）BP神经网络适应性最强，预测精度最高，误差均小于0.5%。

4 结论

1）将BP神经网络预测模型应用于不同CO2摩尔分数天然气偏差因子的计算，为含CO2天然气偏差因子计算提供了一种新的方法。

2）偏差因子计算模型对比结果表明，常规的偏差因子计算方法适用于CO2摩尔分数低于50%的天然气，对CO2摩尔分数超过50%的天然气，误差均较大。

3）BP神经网络适应性最强，对所有样品的相对误差均小于0.5%，验证了该方法的精确性。

［1］杨继盛，刘建仪.采气实用计算［M］.北京：石油工业出版社，1994：7-8.

［2］Wichert E，Aziz K.Calculation of Z for sour gases［J］.Hydrocarbon Processing，1972，51（5）：119-122.

［3］郭绪强，阎伟，陈爽，等.特高压力下天然气压缩因子模型应用评价［J］.石油大学学报：自然科学版，2000，24（6）：36-38.

［4］张庆洲，樊建明，郭平，等.非烃对气藏流体偏差系数的影响［J］.天然气工业，2009，29（10）：74-76.

［5］王刚，杨胜来.富含CO2天然气偏差因子研究［J］.石油钻采工艺，2010，32（1）：53-56.

［6］郭肖，杜志敏，杨雪峰，等.酸性气藏偏差因子计算模型［J］.天然气工业，2008，28（4）：89-92.

［7］汪周华，郭平，李海平，等.酸性天然气压缩因子实用算法对比分析［J］.西南石油学院学报，2004，26（1）：47-50.

［8］汪周华，郭平，周克明，等.罗家寨气田酸性气体偏差因子预测方法对比［J］.天然气工业，2004，24（7）：86-95.

［9］Piper L D，McCain W D Jr，Corredor J H.Compressibility factors for naturally occurring petroleum gases［R］.SPE 26668，1993.

［10］韩力群.人工神经网络理论、设计及应用［M］.北京：化学工业出版社，2002：5-6.

［11］任双双，杨胜来，沈飞.BP神经网络预测最小混相压力［J］.断块油气田，2010，17（2）：216-218.

［12］范照伟，杨胜来，王玉霞，等.火山岩高含CO2气藏渗透率应力敏感性研究［J］.断块油气田，2010，17（1）：57-59.

［13］陈林，孙雷，彭彩珍，等.注CO2井筒温度场分布规律模拟研究［J］.断块油气田，2009，16（6）：82-84.

［14］李士伦.天然气工程［M］.北京：石油工业出版社，2000：8-9.

［15］张楠，许巧娟.富含CO2天然气偏差因子计算模型及影响因素研究［J］.天然气勘探与开发，2013，36（3）：61-64，69.

［16］徐朝阳，熊钰，谢恩，等.酸性天然气偏差因子计算方法优选［J］.重庆科技学院学报：自然科学版，2012，14（1）：23-26.

［17］伍勇，杜志敏，郭肖，等.异常高压气藏偏差因子计算方法［J］.天然气工业，2008，28（6）：92-93，100.

［18］黄德明，付德奎，胡杰，等.高酸气田天然气偏差因子计算方法［J］.天然气技术与经济，2012，6（6）：30-33.

［19］阳建平，肖香姣，张峰，等.几种天然气偏差因子计算方法的适用性评价［J］.天然气地球科学，2007，18（1）：154-157.

［20］胡建国，郭分乔，许进进.计算天然气偏差因子的DAK方法的修正［J］.石油与天然气地质，2013，13（1）：120-123.