基于改进遗传算法的装配序列优化

阎树田, 贾晓锋、, 贺成柱, 陶燚

(1.兰州理工大学 机电工程学院,甘肃 兰州730050;2.甘肃省机械科学研究院,甘肃兰州730030)

0 前言

装配序列规划在产品装配设计中扮演着重要的角色,装配序列的选择直接关系到产品的装配效率和品质[1]。序列规划[2]就是在给定产品设计方案的情况下,探索合理可行的装配序列,并从中选出最优的序列,用以指导产品的装配,达到预期的目标。在装配序列规划研究中,最新的研究成果主要表现为:基于现代优化算法进化生成可行的装配序列等;基于人机交互方法,通过将人的主动决策和装配知识导航相结合求解装配序列;基于知识求解装配序列等[3－7]。这些方法的主要目的是生成结果接近或达到最优的装配序列。装配序列规划通过对装配信息的分析、提取、总结生成可行的序列规划,可以提高装配能力,缩短装配时间,降低装配成本,提高装配精度,增加装配的可靠性,减少产品的上市时间。

1 改进遗传算法

1.1 装配序列规划问题

装配序列规划的目标是求解满足各种装配约束条件,得出具有最优的可行装配序列[8]。在产品装配过程中,一旦出现违反零件之间的装配几何约束关系,必将出现装配零件的相互干涉,影响装配效率。操作换向、装配工具及装配类型等都是影响装配效率的主要因素。在企业追求快速反应的时代,产品在装配过程中,装配方向的改变,装配工具的更换以及装配类型的改变都直接影响装配辅助时间,也增加产品的生产成本,使产品在竞争中处在不利的地位。

1.2 染色体的定义

复合基因称为基因组片的编码技术,每个基因组片包括多个位码,主要考虑4个特征元素:零件个数N,装配工具T,装配方向D,及装配类型L。

Ni代表零件,Ti代表装配工具,Di代表装配的可行性方向,装配方向只考虑与坐标轴平行的＋x,－x,＋y,－y,＋z,－z6个方向(本文中出现两个零件的装配方向与x,y,z有一定夹角,特进行简化处理,以与夹角小的方向为准),Li代表零件的装配类型,主要是面贴合,插入,轴对齐,焊接和铆接等。

单个基因组的构成,包括四个子段,Ni,Ti,Di,Li,例如(3123)这个基因组,代表的意义就是编号为3的零件,选用工具1,在＋y方向上,按第3种装配类型进行装配。图1表示每条染色体由n个基因组构成。染色体的变异主要是各个基因组之间的变异。在进行进化时,主要是零件的装配方向,装配工具,装配类型参与变异计算,进而实现整个装配过程的进化,计算结果直接是整个装配过程的信息完备,算法收敛较快,效率较高。同时在计算时,又充分利用遗传算法的鲁棒性强的特点,即不需要过多外部信息,通过适应度函数进行评价,得出最优序列。

图1 基因组片组成的染色体

1.3 算法步骤

1)确定实际问题参数:装配零件数目n,染色体长度,并对基因进行编码。

2)设定初始种群大小,交叉概率Pc,基因组变异概率Pm。

3)产生初始种群,并作为父代的种群。

4)输入装配体的干涉矩阵,匹配特征信息,从几何约束和工艺约束判定初始种群的可行性,并计算适应度值。

5)进行遗传操作,交叉和变异。

6)产生新一代种群,进行适应度函数的计算。

7)设定适应度条件,判断是否满足条件。

8)不满足终止条件时,从种群中两两选择不同的个体作为父代转入步骤3。

9)满足条件时,输出序列。

适应度函数主要进行评价的要素有几何约束和工艺约束,几何约束可以排除发生几何干涉的序列,减小解的空间;工艺约束主要包括装配方向,装配工具,装配类型等工艺信息,在实际生产装配过程中这些都对装配成本具有重要的影响。适应度函数:

nt装配时更换工具的次数,nd装配时零件的换向次数,nl零件装配类型的变化次数。ωt是更换工具次数的加权系数,ωd更换装配方向次数的加权系数,ωl装配类型变化次数的加权系数。初始种群的产生可以通过多种方式,如专家给出,随机设定,虚拟环境下的人工拆卸,或由以上基本方式综合得到。

1.4 遗传算子

遗传计算中包括选择算子、交叉算子、部分匹配交叉算子、次序交叉算子和变异算子。交叉和变异既相互配合又相互竞争使算法的搜索能力得到了提高,交叉算子的实质就是父代与母代的基因组片进行重组产生后代,使后代具有双亲的遗传特征,本算法采取轮盘赌选择,改进部分匹配交叉算子和变异算子,图2所示为改进算法部分匹配交叉算子示意图。

图2 部分匹配交叉算子示意图

1.5 建立干涉矩阵

在装配过程中,为了使遗传算法快速收敛,减少不必要的变异计算,在遗传算法中加入了干涉矩阵,其主要是确定各个零件的装配序列几何可行性及可装配方向,干涉矩阵I:

假设有n个零件参与装配,那么干涉矩阵就是一个n行,3n列的矩阵,其元素Iijz表示零件j沿＋z方向装配与零件i的干涉情况,具体取值判定规则:如果零件j沿＋z方向装配到位时与零件i发生干涉,则Iijz＝1;反之,则Iijz＝0。零件j沿－z方向装配与零件i干涉的情况,与零件i沿＋z方向装配与零件j干涉的情况相同,由元素Ijiz表示。按照这种方法,可以确定Iijx和Iijy的值。每个零件在空间坐标系中考虑＋x,＋y,＋z,－x,－y,－z这六个方向的装配干涉情况,对图3中马铃薯种植覆膜机减速器中标注的序号1~12的零件的干涉矩阵进行列举如下矩阵所示,由于受篇幅限制其余13个零件的干涉矩阵按照上述判断方法可以得出:

1.6 装配方向的确定

对一个零件i的装配方向进行分析时,主要是根据已经装配好的上一个零件决定,根据下面布尔或运算公式进行判断:

Iij对应干涉矩阵中各个元素,U表示矩阵元素的求或运算,在三维坐标,根据式(3)~式(8)对图3中的马铃薯种植覆膜机的减速器装置进行分析得到的可装配零件方向如表1所示。

表1 装配体中零件的可行方向

2 实例分析

结合马铃薯种植覆膜机的减速器装置进行分析,在对装置进行分析时对装置进行了适当的简化,把部分零件进行了删减,并对过于重复的零件进行了整合,具体如图3所示,共整合标注成25个零件。

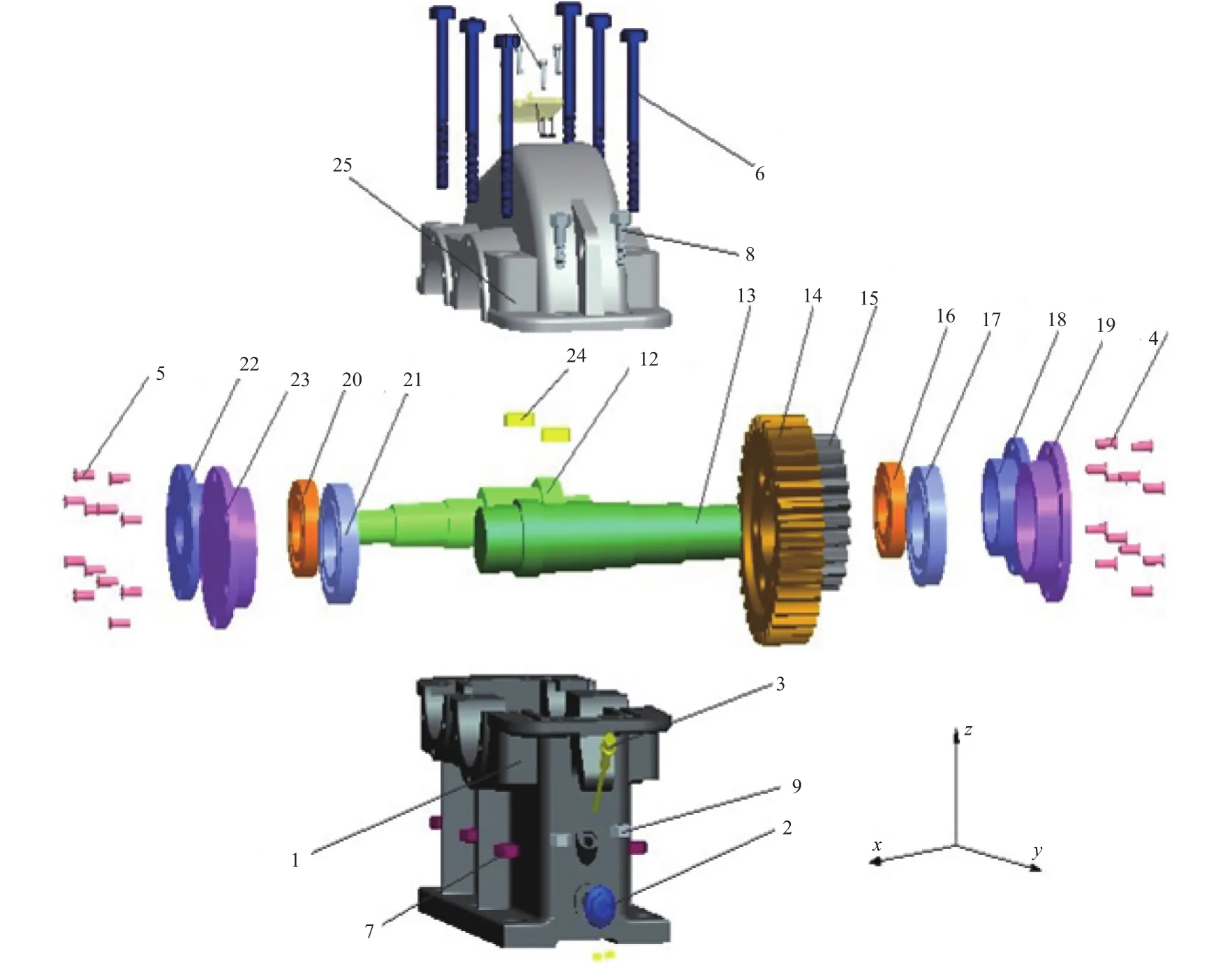
图3 马铃薯种植覆膜机减速器

叠加代数取100,初始化选择率,交叉率和变异率分别设置为0.7,0.8和0.3。从运行过程中得到如表2两种算法对比表,并得出改进算法优化后的最优装配序列如表3所示。

表2 遗传算法与改进遗传算法的结果对比

由表2遗传算法与改进遗传算法的结果对比可以看出,加入干涉矩阵和添加装配零件的装配方向,装配工具和装配类型等约束信息,通过几何约束和工艺约束,排除不可行的装配序列,缩小解空间,使算法快速收敛,能在较短的时间内实现最优序列,达到预期的改进效果。实验结果表明改进算法具有收敛快,效率高,实用性强的优点。

表3 装配序列优化结果

3 结语

如何有效综合利用几何知识,算法和实际装配常识等,使序列求解的功能和效率达到满意的结果是改进算法目的。改进算法主要加入了干涉矩阵和装配匹配特征,在运算中直接排除了许多不合理的装配序列,由表2遗传算法与改进遗传算法的结果对比可以看出,改进遗传算法具有较好的收敛性能,能在较短的时间内搜索到最优装配序列解。改进算法是装配序列规划问题高效求解的一个方向,如果能在算法中自动识别各零件的装配稳定性,同时突破有关机械装配的传统观点,从系统化、自动化和智能化的新角度进行研究,对装配序列规划有很大的现实意义,这也将是今后研究的重点内容。

[1]宁黎华,古天龙.装配序列规划问题求解的一种混合算法[J].计算机集成制造系统,2007,13(4):762-767.

[2]杨鹏,刘继红,管强.面向装配序列优化的一种改进基因算法[J].计算机集成制造系统,2002,8(6):467-471.

[3]邓明星,唐秋华,雷喆.基于蚁群算法的改进装配序列规划方法[J].武汉大学学报(工学版),2013,46(2):246-251.

[4]敬石开,李连升,曾森,等.面向产品装配序列规划的智能优化算法库[J].计算机辅助设计与图形学学报,2010,22(9):1593-1599.

[5]彭涛,李世其,王峻峰,等.基于增强人机交互技术的虚拟装配[J].计算机辅助设计与图形学学报,2009,21(3):354-361.

[6]邢彦锋,来新民,金隼,等.改进遗传算法在装配操作优化中的应用[J].计算机辅助设计与图形学学报,2007,19(10):1298-1302.

[7]宁汝新,郑轶.虚拟装配技术的研究进展及发展趋势分析[J].中国机械工程,2005,16(15):1398-1403.

[8]张烨,宁汝新,刘检华.面向虚拟装配的装配序列规划技术研究[J].计算机集成制造系统,2006,12(1):90-9.