在ANSYS中模拟功能梯度材料的方法研究

郑 波 冯是全

(上海海事大学物流工程学院，上海 201306)

在ANSYS中模拟功能梯度材料的方法研究

郑 波 冯是全

(上海海事大学物流工程学院，上海 201306)

介绍一种在ANSYS软件中模拟功能梯度材料的方法。对于功能梯度材料板，考虑到其弹性模量E和泊松比v都是沿长度方向变化的函数。可以将板用三角形单元离散化，求出每个三角形单元的等效模量和泊松比，再用命令流的方法赋予每个单元，则可以实现在ANSYS中对功能梯度材料板的模拟。

功能梯度材料;有限元;等效弹性模量

功能梯度材料(Functionally Graded Materials，FGMs)一般由两种物理性质完全不同的材料(比如金属和陶瓷)复合而成。从宏观上看，每种组份的分布在空间位置上是连续变化的，因此这类材料的力学和热学参数没有突变和奇异点，因而大大缓解了应力集中。另外，功能梯度材料是可设计的，可以通过改变组分的空间分布情况而优化其热学、力学等性能。这类材料在航天航空、核反应堆、内燃机和燃气机等领域中具有广阔的应用前景。

现在，许多学者在功能梯度材料的研究上已经取得了富有成效的进展。由于功能梯度材料是一种微观和宏观结构方面都非均匀的特料，其微观组成的梯度变化使得这种材料明显不同于具有均匀宏观结构和性能的常规复合材料，所以在ANSYS建模的时候不能够直接在材料属性中设置其弹性模量E和泊松比v。本文希望运用等效弹性模量的方法实现在ANSYS中对功能梯度材料的模拟。

1 等效弹性模量和等效泊松比的建立

一般情况下，物体的变形同时包含了体积改变和形状改变。因此，总应变能密度包括体积改变能密度和畸变能密度两种。即：υε=υv+υd

根据材料力学的理论，微元体在三向等拉应力状态下只发生体积改变且体积改变能密度为：

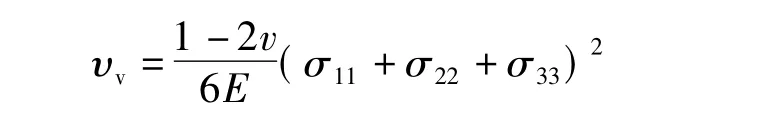
反之，当微元体受三向大小为主应力与平均应力之差的等效拉应力时，微元体只发生形状改变而没产生体积改变，其畸变能密度为：

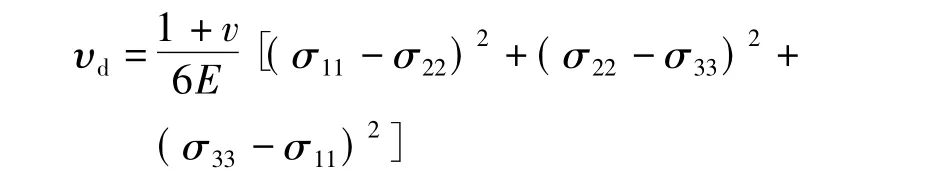
对于平面问题，σ33=0。所以上面2个等式简化为：

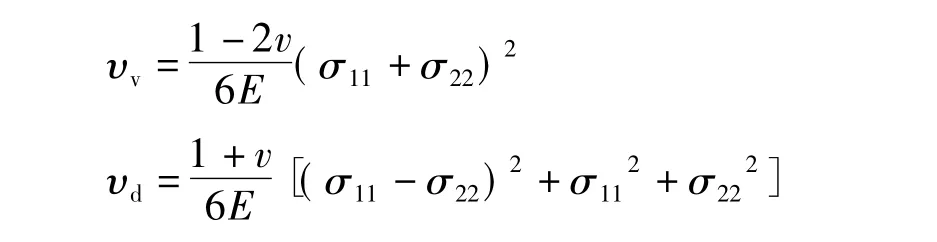
对于功能梯度材料板而言，由于其弹性模量E和泊松比v是关于x和y的函数，E=E(x，y)，v=v(x，y)，设板厚为 t，单元面积为 A，等效弹性模量为Eeq，等效泊松比为veq。所以在平面三角形单元中，单元的体积改变能与形状畸变能之和与等效弹性模量和泊松比所产生的体积改变能和形状畸变能相等。即有

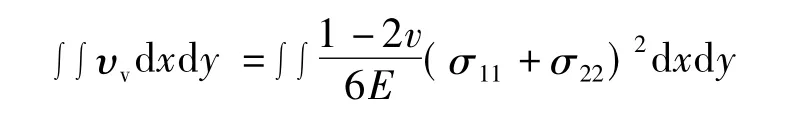
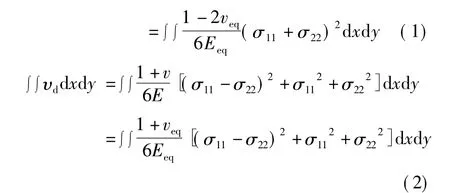
因为等效弹性模量Eeq，等效泊松比veq，σ11，σ22都为常数，所以上面二个公式通过求解可以得到：

通过公式(3)可以算出各个单元的等效弹性模量Eeq和等效泊松比veq，据此可以在有限元软件ANSYS中建立模型。

2 算例

设有一矩形功能梯度材料薄板，长为L=1 m，宽为 w=0.4 m，厚度为 t=0.003，其弹性模量和泊松比均为关于坐标的函数，假设E=1.8+0.2e0.8(x1－8)×1011Pa，v=0.3e0.1(x1－8)。

在没有定义各三角形单元的材料属性之前，在ANSYS软件的Plot Numbering Controls中设置Material numbers显示如图1。

则功能梯度材料板中各单元的编号显示如图2。

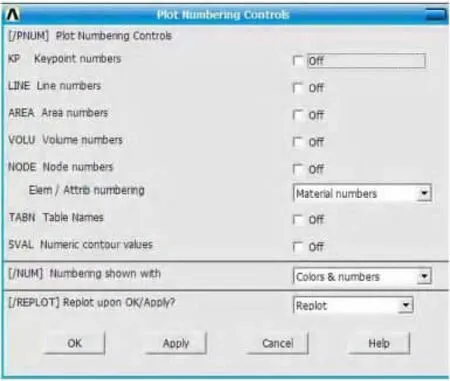
图1

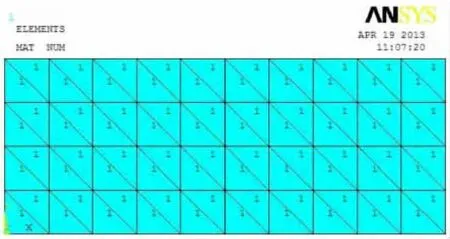
图2

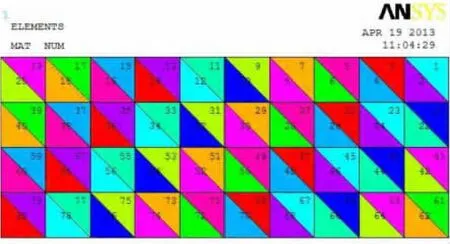
图3

而通过等效弹性模量的方法，分别求出每个三角形单元的弹性模量之后，以命令流的形式赋予各单元，则在ANSYS的Plot Numbering Controls中设置Material numbers显示如图3。

3 结论

通过对比可以看出，用等效弹性模量赋予每个三角形单元之后，每一个单元的材料属性是不一样的，从而说明这种用等效弹性模量的方法来模拟功能梯度材料是可行的。而如果要更准确地模拟功能梯度材料板的话，可以把三角形单元划分地更细一些，从而提高求解的精度。

［1］张骥华.功能材料及其应用.北京：机械工业出版社，2009：458－462.

［2］胡于进.有限元分析及应用.北京：清华大学出版社，2009：48－51.

［3］ShiWeichen，On the dynamic energy release rate in functionally gradedmaterials［J］.International Journal of Fracture 2005，131(3)：31 －35.

［4］王勖成.有限单元法［M］.北京：清华大学出版社，2003.

编辑 傅冬梅

Research on Simulation Method of Functionally Graded Materials by ANSYS

Zheng Bo，Feng Shiquan

The simulativemethod of functionally graded materials by ANSYS software has been introduced.For elastic modulus E and Poission’s ratio v of functionally graded materials sheetare variable functions along length direction，triangle units used for the sheet are supposed to make discretization and work out equivalentmodulus and Poission’s ratio of each triangle unit，furthermore each unitwas provided with command flow means，finally simulation of functionally graded materials sheet by ANSYS could be realized.

functionally graded materials;finite element;equivalent elasticmodulus

O242.21

A

2013—04—22