一种多小区OFDMA系统中有效公平的资源分配方法

段博文，蔡跃明，魏 毅，杜家华

(1．解放军理工大学 通信工程学院，江苏 南京210007;2．71960部队司令部，河南信阳464000)

全频率复用——同时利用每个小区的所有的子载波——已成为4G网络规划部署的主要目标［1］。而全频率复用必定会带来小区间干扰，这正是限制无线通信系统吞吐量的主要原因［2］。在多小区系统场景中，一个主要的研究热点就是考虑通过怎样控制来自邻小区的同道干扰来优化系统性能［3］。如今，分布式资源分配技术已越来越契合现代通信网络的需求，许多研究人员已经开始借助博弈论来寻求资源分配和干扰协调问题中令人满意的解［3，5－7］，这是因为源于经济领域的博弈论天然地适用于无线通信系统的分析与建模。现存的许多文献研究的都是下行链路，在文献［4］中，作者提出了一种多天线OFDMA系统优先级排序和贪婪理论结合动态分配资源的方法。在文献［7］中，作者利用非合作博弈理论提出了一种发射功率自适应的方法来减小OFDM系统中的小区间干扰。通过用博弈论的方法找到每个通道用户的最优发射功率，系统的吞吐量得到了提升，但这篇文献并没有考虑这种场景下的子载波分配问题。

目前有关博弈论的工作主要注重功率控制，功控问题利用连续博弈方法能够很容易地解决。而利用博弈论进行子载波的分配，或多或少被简化甚至被忽视，并且用来解决子载波的分配问题要更加困难。因此本文利用联盟形成和纳什讨价还价解研究了上行OFDMA系统中多小区分布式子载波分配的博弈问题。

1 系统建模

考虑一个有M个基站的上行OFDMA系统，记为M={1，2，…，l，…，M}。可用的频谱资源划分为K个子载波。用户集合和子载波集合分别记为N={1，2，…，n，…，N }和K={1，2…，k，…，K}。N=，指集合N的元素个数，K=，指集合K的元素个数。每一个基站m∈M都有一个用户子集Nm⊆N，其中∪mNm=N，以及子载波集合Km，其中Km=K，∀m∈M。

定义信道增益矩阵H=RN×N×K，其中hkij是指使用子载波k时发射用户i和接受用户j之间的信道增益。规定hkij≠hkji。hkii指使用子载波k时发射用户i到基站的信道增益。类似地定义发射功率矩阵为P=RN×K，其中元素pik指第i个发射用户在第k个子载波上的功率，而且必须满足非负的限制。另外，用户i总的发射功率不能超过。定义子载波分配矩阵为A∈{0，1}N×K，其元素aik=1为用户i用子载波k来传输信息，否则aik=0。用户和基站都分别配备一根发射天线和接收天线。第m个小区用户i在子载波k上的容量为，其中是信干噪比，Γ=－ln(5BER)/1.5是误比特率间隔。

2 纳什讨价还价解(NBS)

限于篇幅，本文略去对 NBS基本概念［8－10］的阐述。本文直接阐明如何将这种方法应用于OFDMA系统中的子载波分配。

在一个优化问题中，帕累托最优点可能有多个，那么一个不能回避的问题是:应该寻找并采用哪个帕累托最优点。在本文中，主要是以资源共享的公平性来选择帕累托最优点。在所有用户的最小需求满足之后，余下的资源根据各个用户的信道条件将其成比例地分给每个用户。而这正是纳什讨价还价(NBS)解的优点，它在一定条件下能得到一个唯一又公平的帕累托最优点。下面简要介绍NBS的相关概念:

定义1:若效用集U⊂RN是RN的闭凸子集，那么纳什讨价还价解可以通过以下优化问题来获得［9］

在本文中，效用函数U定义为每个用户所能获得的信道容量，即Ui=Ri=∑kRik，目标就是在最大化用户容量的同时保证对所有用户的公平。

3 基于纳什讨价还价解的分布式子载波分配算法

3.1 算法描述

显然，式(1)描述的问题是一个NP－hard问题。许多文献是用集中式方法来解决这种问题，而当用户和子载波数目大的时候，集中式算法的计算复杂度非常高。这一节提出了一种能获得NBS的分布式子载波分配算法。与文献［10］类似，算法先解决两用户情形，然后再推广到多用户系统。在多用户系统中，用户先两两结成联盟，然后对每个联盟使用先前的两用户的算法，来进行子载波的交换。最后，用户将一次次地重组联盟并重新合作协商，直至性能不再提升。

3．1．1 联盟形成

为了避免计算复杂度太高，本文采用文献［10］中的思想。如果用户的总数是偶数，则用户两两结成联盟。否则，假设额外存在一个“哑”用户来确保用户总数是偶数，任何用户都不能与这“哑”用户交换资源。另外，算法中的两人联盟是在各个小区中随机形成的，因此只要是能使性能提升的两人组合都将会考虑进来。

3．1．2 对子载波进行讨价还价

一旦两人联盟形成，讨价还价就开始了。就像在集市讨价还价一样，两个用户可以协商并互换自己的资源——子载波——来使自己获益。所有构成联盟的子载波——用户的排列组合都应进行比较，从而得出哪一个匹配能产生最高的用户速率。显然，每个联盟中的计算不需要联盟与联盟之间交互信息，因此这个算法是分布式的。然而，由于这种操作的复杂度比较高，用穷举法搜寻最优用户，子载波匹配是不可行的。因此本文设计了一种有效的算法来交换用户的子载波，这实质上解决的是一个复杂的整数规划问题。即先将子载波进行排序，然后用“两段分”的方法为两个用户分配子载波。

1)算法1:两用户的子载波分配

(1)初始化。以最小速率需求来初始化子载波分配，初始化λ1=1和λ2=1。

(2)对子载波进行排序，根据的值从大到小对子载波进行排序。

(3)用户1使用第1至j个子载波，用户2使用第j+1至N个子载波。为了简便，假设功率是平均分配在用户使用的子载波上的，计算U=(Ri－)。

(4)观察每一个j对应的分配方案能产生的效用，选择能产生最大效用U的“两段分”子载波分配方案，并计算对应的R1和R2。

(5)更新信道分配。更新 λ=，λ=12。继续第(2)步，直至效用U不再提升。)

2)算法2:多用户的子载波分配

(1)初始化:所有子载波随机分给用户。

(2)联盟形成:每个小区里随机地形成两人联盟。

(3)在每个联盟中进行讨价还价(此步骤进行算法1)。

(4)重复:重复第(2)步和第(3)步，直到没有性能的提升。

定理1:对于多用户的情形，如果效用集(U1，U2，…，UN)对任意两个用户是帕累托最优，那么这个效用集对小区内所有用户都是帕累托最优的。

证明:假设(U1，U2，…，UN)对所有的用户来说不是帕累托最优，那么必定存在另外一个点(U'1，U'2，…，U'N)使得U'i≥Ui，∀i和U'i＞Ui，∃i(假设是用户k，U'k＞Uk)。因此，对于两个用户k和j(j≠k)，效用点(U1，U2，…，UN)就不是帕累托最优，这与先前的假设相矛盾。证毕。

因为不同小区里的用户是不能交换其子载波的，只有属于相同小区的用户可以形成联盟并相互讨价还价。应此在多用户系统中，同一个小区里的一个效用点对任意两用户都是帕累托最优的话，这个效用点对这个小区的所有用户都是帕累托最优的。

3.2 收敛性分析

在每一次迭代过程中，优化函数R的值是不会下降的。而每个用户的先用函数值Ri有上界。所以，本文提出的算法必定收敛。

3.3 复杂度分析

在每一次迭代中，算法的复杂度为O(N2)，本文可以利用文献［10］中所用的二进制搜索算法进一步将其降至O(NlogN)。

4 仿真结果与分析

本节对改进的子载波分配算法进行了仿真。考虑3小区的OFDMA系统。与文献［6］中类似，每个蜂窝小区半径100 m，且各个小区都有12个用户随机地均匀分布。基站位于小区中心，相互之间间隔 1 00m。两用户之间的路径损耗表示为hij=0.097/，其中 υ =4是发射用户i到接收用户j之间的距离。对于用户i，j和子载波k，信道增益为gkij=hij，其中 βk～CN(0，1)服从瑞利衰落。为了简便，令Γ=1，并在仿真中利用==lb(1+)做容量的比较。高斯噪声方差σ2为10－10W。用户的最大功率限制设为0．2 W。

先对各用户进行随机的子载波分配初始化，然后各用户通过相互间的合作协商寻求各自性能的提升。图1展示了改进的子载波分配算法导致的用户容量的提升与迭代次数的关系，并且分别考虑了存在8个、32个和64个子载波时的12个用户的OFDMA系统。从图中可见容量值随迭代次数的增加不断提升，最后稳定于某一速率值。另外从图中得知，随着子载波数目的增加，由于频率分集的提升，系统容量也会随之上升。

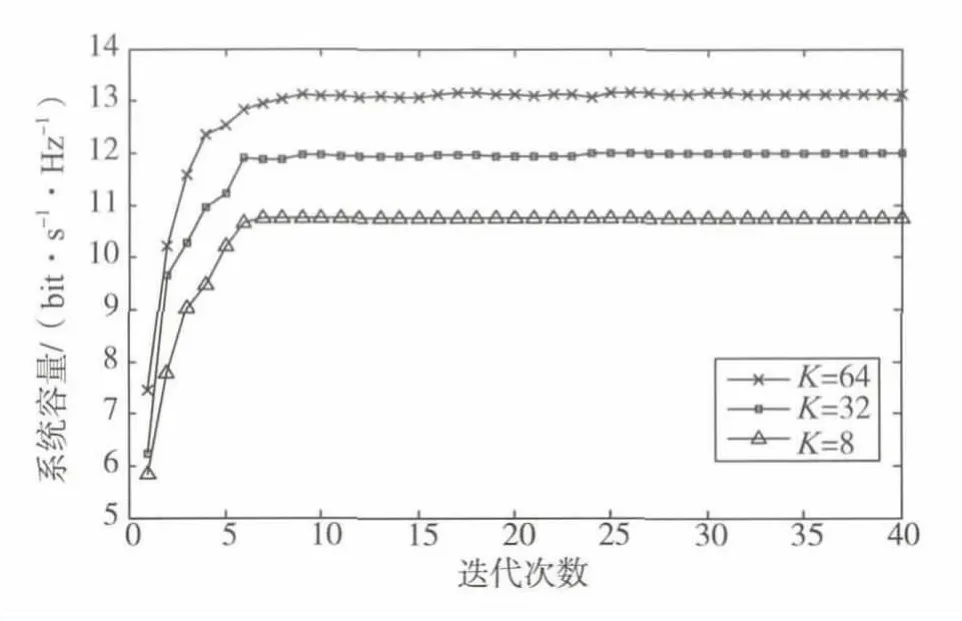
图1 系统容量与迭代次数的关系

在图2中，将本文的算法(Algorithm 1)和另外两种算法(Algorithm 2，Algorithm 3)进行了对比。算法2是指每个子载波根据其用户的信道条件进行分配，算法3是指每个用户分有相同数目的子载波。另外，本文对3种算法都进行等功率分配，并固定子载波数目为64个。图2展示了系统容量与用户数目变化之间的关系，表明了本文所提算法的性能比较优越。

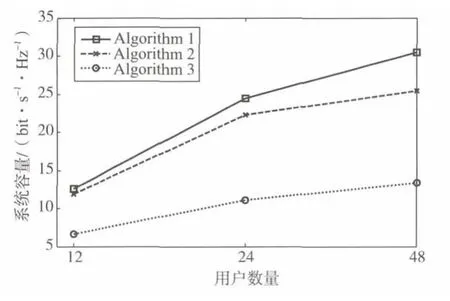
图2 系统容量与用户数量的关系

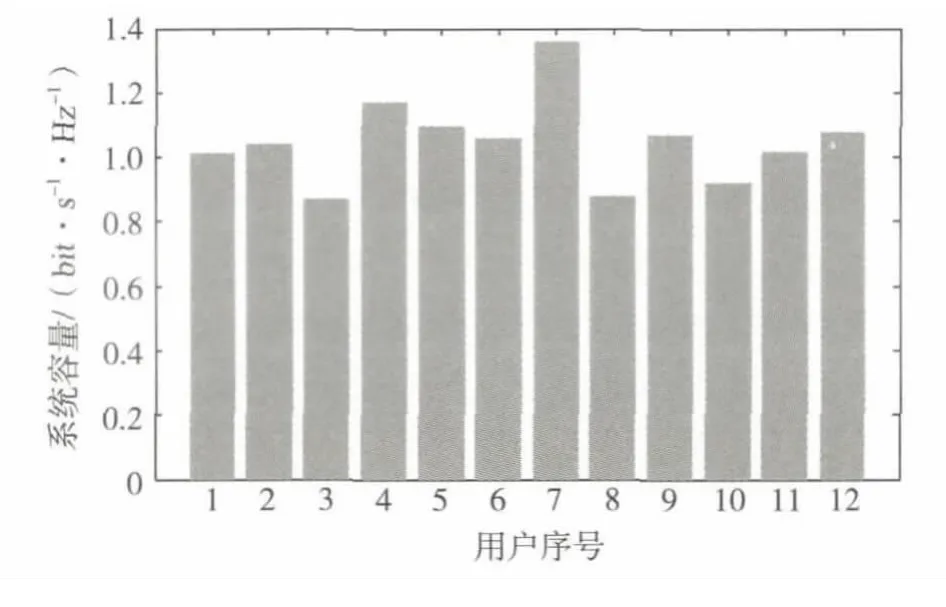
图3 不同用户的容量比较

5 结论

本文研究了多小区OFDMA系统因同道干扰导致的系统容量受限问题，提出了一种底复杂度且有效的子载波分配算法。本文的研究目标是在控制同道干扰的同时最大化系统性能。本文所提算法基于合作博弈概念，即用户先结成联盟再对子载波进行讨价还价。这种算法的全分布式特性非常适用于多小区干扰协调场景。仿真结果表明本文所提算法具有快收敛、明显的容量提升以及良好的公平性3种优点。下一步工作，将关注与同时优化功率和子载波分配，从而期望能达到更高的系统吞吐量。

:

［1］ CHENG Shinming，LIEN Shouyu．On exploiting cognitive radio to mitigate interference in macro/femto heterogeneous networks［J］．IEEE Wireless Communications，2011，1(3):40－46．

［2］ YANG Kai，PRASAD Narayan，WANG Xiaodong．An auction approach to resource allocation in uplink OFDMA systems［J］．IEEE Trans．Signal Processing，2009，57(11):4482－4496．

［3］ KWON Hojoong，LEE Byeonggi．Distributed resource allocation through noncooperative game approach in multi－cell OFDMA systems［C］//Proc．IEEE ICC．Istanbul:IEEE Press，2006:4345－4350 ．

［4］司钊，张静，董建萍，等．多天线OFDMA系统的动态子载波与功率分配方法［J］．电视技术，2009，33(S2):179－182．

［5］ HAN Zhu，JI Zhu，LIU K J R．Non－cooperative resource competition game by virtual referee in multi－cell OFDMA networks［J］．IEEE Journal on Selected Areas in Communications，2007，25(6):1079－1090．

［6］ AL－ZAHRANI A Y，YU F R．A game theory approach for inter－cell interference management in OFDM networks［C］//Proc．IEEE ICC．Kyoto:IEEE Press，2011:1－5．

［7］ TAN C K，SIM M L，CHUAH T C．Blotto game－based low－complexity fair multiuser subcarrier allocation for uplink OFDMA networks［EB/OL］．［2014－02－10］．http://jwcn．eurasipjournals．com/content/2011/1/53．

［8］ ZHOU L．The Nash bargaining theory with non－convex problems［J］．Econometrica，1997，65(5):681－685．

［9］ ZHU HAN，ZHU JI，LIU K J R．Fair multiuser channel allocation for OFDMA networks using Nash bargaining solutions and coalitions［J］．IEEE Trans．Communications，2005，53(8):1366－1376．

［10］ VATSIKAS S，ARMOUR S，VOS M D，et al．A distributed algorithm for wireless resource allocation using coalitions and the Nash bargaining solution［C］//Proc．IEEE VTC．［S．l．］:IEEE Press，2011:1－5．