基于POMDP的次用户多时隙信道选择算法
张红霞,孟东霞,姜志旺
(河北金融学院信息管理与工程系,河北保定 071051)
目前,认知无线电(Cognitive Radio,CR)被广泛用于解决频谱管理方式中,动态的频谱环境和静态的频谱分配策略之间的矛盾,频谱资源的不可再生性和授权频段利用率不高之间的矛盾,可分配的频谱资源很少与频谱需求量很大之间的矛盾[1-6]。
POMDP数学工具可以刻画动态频谱环境中时变特性,在POMDP算法模型中,次用户可以通过逐步的学习和调整,以获得最佳的系统性能[7-10]。在本文的系统模型中,为了提升整个系统性能,次用户将以混合接入策略[11]接入信道,以宽带频谱感知模式选择感知多条主用户信道,借助POMDP理论刻画信道选择过程,以实现最大化次用户系统的吞吐量,同时减小计算量的目标,在每一个时隙开始时,次用户选择部分信道进行感知,之后根据感知结果选择不同的传输功率接入信道,对于没有被选定感知的信道,次用户可以直接接入。并求得最优策略和次优策略来求解POMDP问题。
1 系统模型

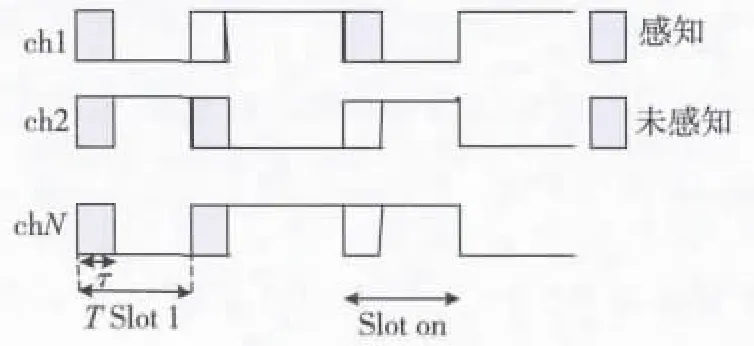
图1 次用户系统结构图
假定一个1×N向量S(m)表示时隙m内所有的主用户子信道的状态,S(m)=[s1(m),s2(m),s3(m),…,sm(m)],m表示时隙编号,m∈{1,2,…,m}。sn(m)=1表示信道n在时隙m被主用户占据,与之相对应,sn(m)=0表示信道n在时隙m空闲。S(m)的状态空间表示为
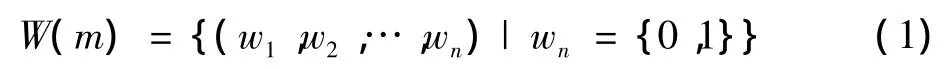
假定Pwn,wn'表示信道n从状态wn跳转到wn'的跳转概率,则

式中:wn'={0,1}。对于信道n,其状态跳转概率分别为P01=βn,P00=1-P01,P10=αn和P11=1-P10。
在每一个时隙开始之前,次用户需要选择一些信道进行检测,假定τn(m)表示信道n在时隙m的感知时间。对于那些没有被选择进行感知的信道,次用户等待相同的时间,与被感知的信道一起接入,以保证信道之间的同步性。鉴于硬件限制,次用户不能在某一子信道上进行信道感知的同时,在另外子信道上进行传输。在感知之后,次用户以混合接入策略接入信道。若是信道n被感知,且感知结果为空闲,则次用户在该信道的传输功率为P1n,若是感知结果为占据,则传输功率为P2n。若是信道n没有被感知,则次用户直接以功率P2n接入,P1n>P2n。次用户在一个时隙内的模型如图2所示。

图2 单个时隙次用户结构图
次用户首先对信道进行感知,在感知之后,次用户根据感知结果进行数据传输。在传输完成之后,若是传输成功,次用户的接收端会发送一个Acknowledgement(ACK信号)给次用户的发射端,若是传输不成功,次用户的接收端则会发送一个Non-Acknowledgement(NAK信号)给次用户。
本文所提出的信道选择算法的目标是在对主用户的干扰处于系统可接受范围内的前提下,最大化次用户系统的吞吐量。假定Ω为感知信道的集合。若是信道n在时隙m被选择进行感知,n∈Ω,则信道可获得的传输速率为
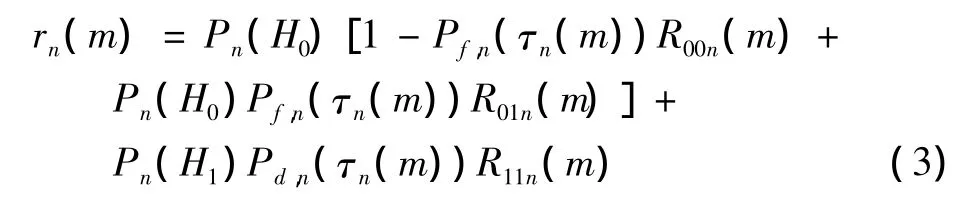
在本文所设计的算法中,由ACK-NCK信道接入模式的使用,当信道为占据,而次用户感知出现错误,感知出的结果却为空闲时,若以较大的功率P1n传输时,则会因为主用户通信对次用户的传输产生干扰,次用户接收端不能接收到数据

若是信道没有被感知,次用户直接接入,则信道的传输速率

则系统模型优化问题就可以表示成

式中,限制条件不但对主用户进行了保护,还能保证次用户选择宽带频谱感知模式来感知信道,各条子信道感知时间一样。Ω是选择感知信道的集合,因为τn(m)是一个连续变量,这样就无法直接对优化问题进行求解。所以,接下来,本文将采用 POMDP[12-13]理论对其进行处理,得出模型的最优解和次优解。
2 基于POMDP信道选择算法设计
在POMDP的架构下,次用户在每个时隙开始之前,根据信任变量和上一个时隙的实际收益值来做出合理的行为,在每一个时隙结束的时候,根据该时隙的行为和所得到的相对应的观测值更新信任变量,为下一个时隙的行为选择提供依据。POMDP算法架构的流程图如图3所示。
2.1 行为(Actions)
在时隙m开始时,次用户的行为包括:判定选择哪些信道进行感知,感知时间长度以及信道的接入功率。假定A(m)为次用户在时隙m的行为向量


图3 POMDP算法架构流程图
式中:A1(m)表示被选择进行感知的信道,A1(m)=[a11(m),a12(m),…,a1N(m)],a1n∈ {0,1}。在时隙m,若是信道n被感知,则a1n(m)=1;反之,a1n(m)=0。τ(m)表示次用户在时隙m各条信道上的感知时间,τ(m)=[τ1(m),τ2(m),…,τN(m)],且各条信道的感知时间相等,τ1(m)=τ2(m)=…=τN(m)。若是次用户直接接入所有的信道,则其感知时间为0。A2(m)表示以功率P1n,P2n接入的信道,A2(m)=[a21(m),a22(m),…,a2N(m)],a2n(m)∈ {0,1}。当信道以功率P1n接入时,a2n(m)=1;信道以功率P2n接入,a2n=0。若是信道没有被感知,次用户直接以功率P2n接入,同样a2n(m)=0。
2.2 观察向量(Observations)
假定O(m)表示次用户在时隙m的观测向量,O(m)=[o1(m),o2(m),…,oN(m)]。在本文给出的模型中,次用户的观测值在信道n中有4种可能,on(m)∈{0,1,2,3}。
1)若是信道n被感知,且感知结果为空闲,次用户以功率P1n接入。在数据传输完之后,次用户发射端收到数据接收的确认信号ACK1,这表明感知结果是正确的。此时,观测值为on(m)=0。
2)在数据传完之后,若是次用户发射端接收到的是信号NCK,这表明感知结果是错误的,次用户的传输被主用户干扰。此时,观测值为on(m)=1。
3)若是信号的感知结果是占据,次用户以功率P2n接入。在数据传输完之后,次用户的发射端接收到确认信号ACK2。此时,观测值为on(m)=2。
4)若是信道n没有被感知,次用户以功率P2n直接接入,其发射端在传输完之后,收到确认信号ACK2。此时,观测值为on(m)=3。
观测值2与3的差别是当on(m)=3,次用户没有对信道进行感知。尽管确认信号是一样的,但是次用户的发射端依旧可以分辨出不同的观测值。
2.3 信任向量(Belief Vector)
在POMDP问题的求解过程中,信任向量可用来在每一个时隙开始时对信道的状态进行推断,其具体表示的是一个基于过去的判决策略和观测值的条件概率。在每一个时隙结束时,信任变量都会根据不同的判决和观测值进行更新,以获取动态环境的准确信息,假定bn(m)为信道n在时隙m的信任向量,bn(m)=[bn,0(m),bn,1(m)],bn,0(m)表示的是空闲概率的条件概率,bn,0(m)+bn,1(m)=1 。
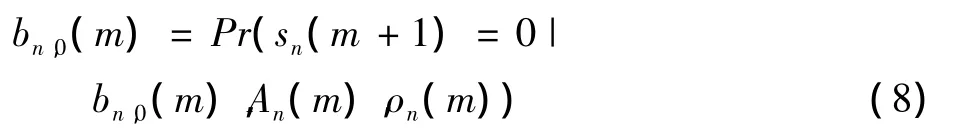


当on(m)=3时,次用户没有对信道进行感知,并不知道信道的确切状态,下一个时隙的信任变量的更新公式表示为

2.4 收益函数(Reward Function)


而在得到其他观测值时,次用户的期望收益值可以表示为
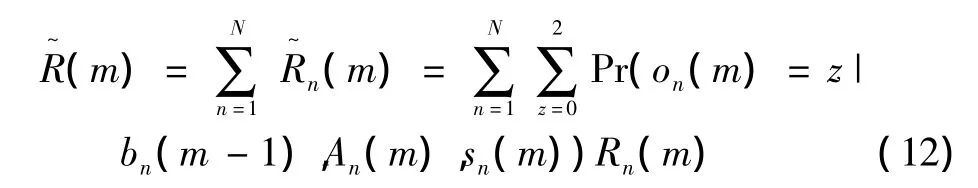
式中:z∈{0,1,2}表示观测值的值空间。
值的条件概率为

它与上一个时隙的信任变量、次用户的行为和信道实际的状态有关系。
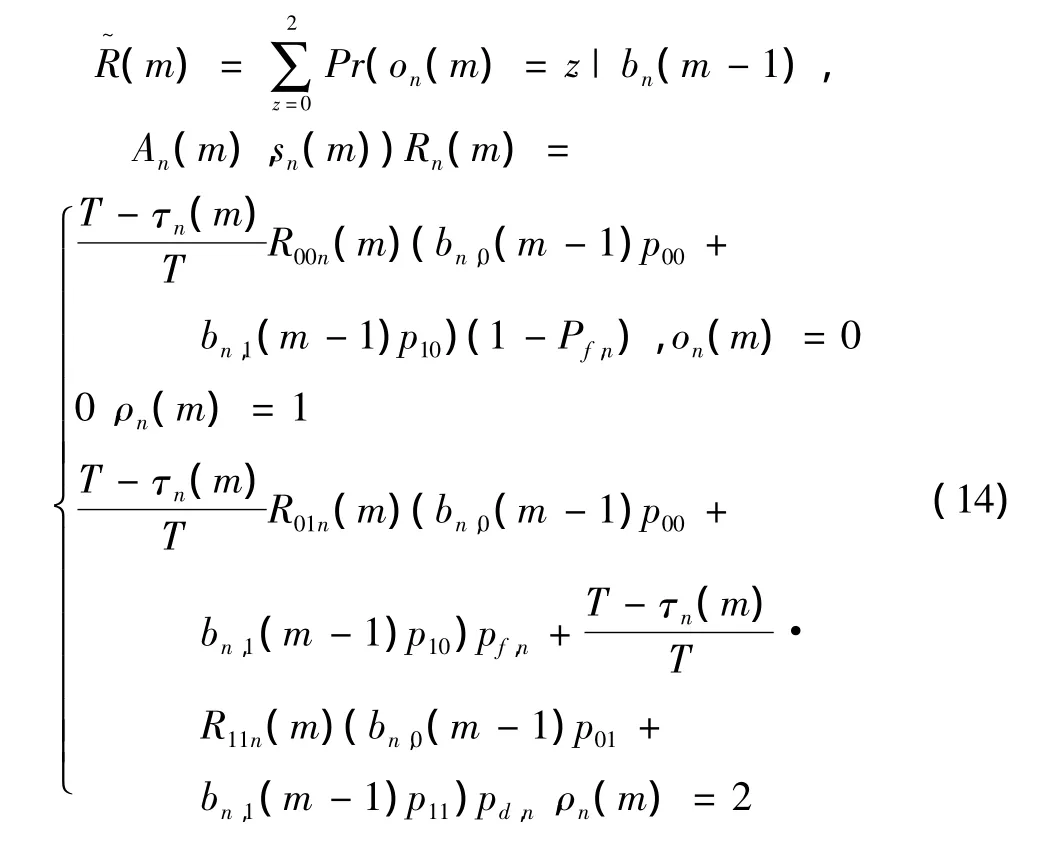
3 POMDP问题求解
基于POMDP的信道选择算法的目的是求解得到一种最优的信道选择与接入策略,以最大化次用户系统在M个时隙的总的吞吐量。基于POMDP的优化问题可以表示为

优化问题P2是一个带约束的POMDP优化问题,这使得其求解需要Intractable Randomized Policy对其进行求解,会带来大量的计算量,计算复杂度很高。然而,可以通过式(15)中的限制条件(若是次用户相信其当前的感知结果,即Pd,n(τ(m))=Pd,th)将P2 转化成无约束的POMDP优化问题。信道n的感知时间可以从式Pd,n(τ(m))=Pd,th获得。此时,问题简化成在每一个时隙开始之前,选择哪些信道进行感知和判断信道的传输功率。子信道之间是相互独立的,为此,可以将次用户系统在多条子信道上的策略简化为多个子信道上策略的集合,即先求出各条子信道上的优化感知与接入策略,然后得出整个系统的优化策略。各条子信道上的优化策略可以各自单独计算得出。
1)最优策略
为了有效地求解信道n的最优策略,这里给出值函数(ValueFunction)Jm(bn(m-1)),表示当信任变量为bn(m-1)时,次用户从时隙m到最后一个时隙M总的最大期望收益值。利用Bellman公式,可得
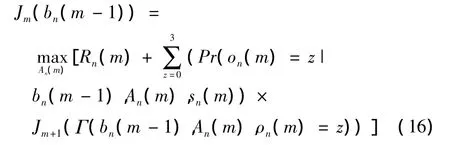
式中:Γ(bn(m-1),An(m),on(m)=z)=bn(m),表示在时隙m结束时信任变量的更新。可由式(14)求得。值函数(16)包含两部分:时隙m的瞬时收益值和时隙m之后的最大期望收益值。最优策略可以通过基于点迭代的算法求解[14]。
2)次优策略
最优策略的求解会带来大量的计算量,特别是当子信道数N很大时。为了减小计算量,降低计算复杂度,提出了一种次优策略。在次优策略中,次用户只是最大化单个时隙内的瞬时收益即可。优化问题的目标函数表示为

次优策略可以有效地在算法计算复杂度和最优解之间取得平衡。此时,优化目标函数会变得简单,可以使用动态规划求得最终解[15-17]。
3)子信道之间的同步性
在上述给出的算法中,与对所有的信道同时进行联合优化不同的是,需要对一个信道进行单独求解最优策略和次优策略。为了将限制性的POMDP问题转化成不带限制条件的问题,令次用户的接入点为Pd,n(τn(m))=Pd,th,这样各条信道的感知时间不一样。然而,在本文所提的算法中,次用户使用宽带频谱感知模式对多条信道进行检测,信道间的感知时间是一样的。为此,存在一个问题:如何来保证子信道之间感知和接入的同步性,即如何在保证信道的感知时间一样的前提下,最大化次用户系统的性能。
为此,本文设定每条信道的判决概率门限值不一样。假定为信道n的判决概率门限值,≥Pd,th。由于感知时间是由公式Pd,n(τn(m))=Pd,th获得,所以,可以将表示成感知时间的函数,即(τ(m))。为了最大化次用户系统的瞬时收益值,同时保证次用户信道间的同步性,可以根据信道间的差异性,调整信道的判决概率门限值。优化问题可以表示为

问题P3中的限制条件不仅保护了主用户,还保证了次用户之间的同步性,且各条信道的感知时间是一样的。依据函数(τ(m))凸函数的特性,限制条件(19)可以转化成感知时间的闭区间。在对闭区间进行离散化之后,次用户可以采用穷举法得到最优的感知时间。感知时间的优化选取可以有效地平衡信道总的瞬时收益最大化与信道同步性的矛盾。
4 仿真实验
在不同的仿真环境下,最优策略和次优策略以及任意策略3种进行数值分析比较,以验证算法的性能。在任意策略中,次用户任意选择信道进行感知,并且信道的接入功率也是任意选择的。3种策略的感知时间是一样的,都是从优化问题P3得到的。主用户的时隙周期是一定的,与次用户的感知周期保持一致,T=10 ms。信道增益是固定的,为了简单起见,假设次用户发射端没有使用自适应调制[18-19]。当传输功率为P1n时,信道的传输速率固定为R00n(m)=0.06 Mbit/s;当传输功率为P2n时,信传输速率R01n(m)=R11n(m)=0.02 Mbit/s。各个子信道的带宽相同,为B=1 MHz,采样频率为fs=2 MHz,判决门限值是εn=1.5;虚警概率门限为Pd,th=0.9,总的时隙数为M=30。
图4表示在不同的信道总数下3种策略中次用户系统的吞吐量比较。这里主要考虑两种情况:N=6和N=2。信道的空闲概率Pn(H0)和信噪比γn,如表1所示。由仿真结果可以看出,次用户在最优策略中的系统性能要比其他两者策略好,并且,当N=6时,最优策略中的系统性能优势变大。这是因为信道的信噪比会影响到信道的感知时间。当信道数较大时,拥有较小SNR的信道会影响到整个系统的感知时间,从而影响系统的吞吐量。在优化策略中,次用户选择一部分信道进行感知,并不是所有的信道都被感知。与次优策略相比,次用户在优化策略中选择更加准确。而在任意策略中,次用户很有可能会选择低信噪比的信道,从而影响到整个系统的性能。当信道数很大时,最优策略中的次用户选择准确性的优势就越明显,次用户能获得的吞吐量就越大。

图4 不同总信道数的次用户吞吐量比较

表1 仿真系数
图5表示在不同的空闲概率差值λ下,次用户系统的吞吐量比较。信道数设为4,λ表示的是两个相邻信道之间空闲概率的差值,Pn(H0)=0.3+(n-1)(0.1+0.05(λ-1))。例如,当λ=1时,信道的空闲概率分别为0.3,0.4,0.5,0.6。由图5可以发现,在不同的信道空闲概率,次用户在最优策略下能获得最优的系统性能。这是因为空闲概率会直接影响到信任变量的更新,在最优策略中,次用户能获得最佳的感知信道和合适的接入功率。

图5 不同相邻信道空闲概率差异值的次用户吞吐量比较
图6是验证次用户系统的吞吐量在次优策略下,最优感知时间和固定感知时间两者的比较。在固定的感知时间算法中,把每一个时隙每一条信道的感知时间固定为τn(m)=2 ms,n∈ {1,2,3,4},m∈ {1,2,…,30}。最优感知时间算法的性能更优越。这是因为在最优感知时间算法中,每一个时隙的感知时间因为被优化,达到了平衡感知的效率与系统吞吐量最大化之间矛盾的目的。
图7表示的是3种接入策略下次用户系统吞吐量的比较。在该仿真实验中,主用户的信道数为4,信道n的空闲概率为Pn(H0)=0.3+0.2(n-1),信噪比为γn=2.1+0.2(n-1),n∈{1,2,3,4}。由图7 可以发现,次用户在混合接入策略下可以获得更多的吞吐量,这是因为在混合接入下,无论感知结果是空闲还是占据,次用户都能以不同的发射功率接入信道,次用户的吞吐量得到有效的提高。
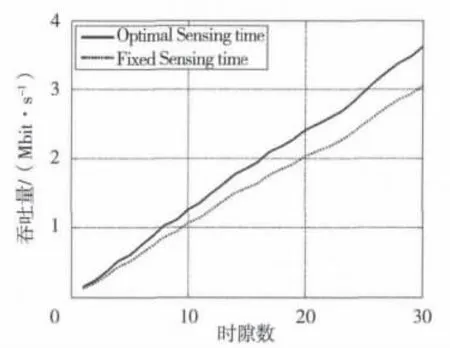
图6 不同感知时间时的次用户吞吐量比较

图7 不同接入策略时的次用户吞吐量比较
5 小结
在动态的频谱环境下,本文提出了一种基于POMDP的信道选择算法。为了最大化次用户系统的吞吐量,同时减小计算量,在每一个时隙开始时,次用户选择部分信道进行感知,之后根据感知结果选择不同的传输功率接入信道,对于没有被感知的信道,次用户直接接入。通过POMDP理论来刻画信道选择过程,并求得最优策略和次优策略来求解POMDP问题。仿真结果验证了算法的有效性。
:
[1]MITOLA J,MAGUIRE G Q.Cognitive radio:making software radios more personal[J].IEEE Personal Communications,1999,6(4):13-18.
[2]MITOLA J.Cognitive radio:an integrated agent architecture for software defined radio[D].Stockholm:Technology,Royal Inst.Technol. ,2000.
[3]HAYKIN S.Cognitive radio:brain-empowered wireless communications[J],IEEE J.Sel.Areas Commu.,2005,23(2):201-220.
[4]王钦辉,叶保留,田宇.认知无线电网络中的频谱分配算法[J].电子学报,2012,40(1):147-154.
[5]郭彩丽,张天魁,曾志民,等.认知无线电关键技术及应用的研究现状[J].电信科学,2006(8):50-55.
[6]王军,李少谦.认知无线电:原理、技术与发展趋势[J].中兴通讯技术,2007,13(3):1-4.
[7]ZHAO Q,TONG L,SWAMI A,et al.Decentralized cognitive MAC for opportunistic spectrum access in Ad Hoc networks:a POMDP framework[J].IEEE J.Sel.Areas Commun.,2009,25(3):589-600.
[8]CHEN Y,ZHAO Q,SWAMI A.Joint design and separation principle for opportunistic spectrum access in the presence of sensing errors[J].IEEE Trans.Information Theory,2008,54(5):2053-2071.
[9]HOANG A,LIANG Y C,WONG D,et al.Opportunistic spectrum access for energy-constrained cognitive radio[J].IEEE Trans.Wireless Communications,2009,8(3):1206-1211.
[10]GONG S,WANG P,LIU W.et al.Maximize secondary user throughput via optimal sensing in multi-channel cognitive radio networks[C]//Proc.IEEE Global Telecommunications Conference. [S.l.]:IEEE Press,2010:1-5.
[11]STOTAS S,NALLANATHAN A.Optimal sensing time and power allocation in multiband cognitive radio networks[J].IEEE Trans.Communications,2011,59(1):226-235.
[12]CHOI K.Adaptive sensing technique to maximize spectrum utilization in cognitive radio[J].IEEE Trans.Vehicular Technology,2010,59(2):992-998.
[13]张国斌.认知无线电系统资源管理与分配关键技术研究[D].广州:华南理工大学,2011.
[14]SMITH T,SIMMONS R.Point-based POMDP algorithms:improves analysis and implementation,available line[EB/OL].[2013-07-07].http://uia.sis.pitt.edu/papers/05/p542-smit.pdf.
[15]ZHAO Q,KRISHNAMACHARI B,LIU K.On myopic sensing for multi-channel opportunistic access structure,optimality and performance[J].IEEE Trans.Wireless Communications,2008,7(12):5431-5441.
[16]ZHANG T,TSANG D.Optimal cooperative sensing scheduling for energy-efficient cognitive radio networks[C]//Proc.IEEE Infocom 2011.[S.l.]:IEEE Press,2011:2723-2731.
[17]张晓,王金龙,吴启晖.认知无线电中基于状态转移概率的感知时隙优化算法[J].通信学报,2011,32(8):72-80.
[18]JIANG H,LAI L F,FAN R F,et al.Optimal selection of channel sensing order in cognitive radio[J].IEEE Trans.Wireless Communications,2009,8(1):297-307.
[19]FAN R F,JIANG H.Channel sensing-order setting in cognitive radio networks:a two-user case[J].IEEE Trans.Vehicular Technology,2009,58(9):4997-5008.

