采用离散粒子群优化的CoMP等功率分配算法
呙 涛,胡国荣
(中国科学院微电子研究所,北京 100029)
LTE-A中为解决小区间干扰问题和增强小区边缘用户的服务质量,提出了协作式多点传输(Coordinated Multipoint,CoMP)技术[1-2]。邻近的几个基站协同为小区边缘的用户提供服务,避免了OFDMA系统中小区间同频干扰,同时也提升了小区边缘用户的服务质量[3]。与传统的无线蜂窝小区相比,由于不同基站的信道不相同,CoMP的功率分配将更具挑战。相应的一系列针对CoMP的功率分配算法被提出来。
文献[4]提出联合注水算法(Joint Water-filling,Jo-WF)并证明其为理论最优,但需要多次迭代才能得到最优解。为简化复杂度,现在的系统中大量采用等功率分配算法(Equal Power Allocation,EPA),但都不同程度地存在不足[5-12]。
粒子群优化算法(Particle Swarm Optimization,PSO)是James Kennedy和Russ Eberhart通过模拟鸟群觅食行为而提出的一种基于群体协作的随机搜索算法[13]。PSO算法最初应用于连续空间的优化,如何应用PSO算法解决离散优化问题引起了人们的注意,出现了一系列的离散PSO(Discrete Particle Swarm Optimization,DPSO)算法,针对0-1规划问题通过将速度作为位置变化的概率,提出了二进制粒子群优化算法(Binary PSO,BPSO)[14]。文献[15]以直觉模糊熵作为粒子群状态测度和速度变异的基本参数,同时加入了位置变异策略。DPSO算法在电力系统、典型组合优化难题等领域中得到应用研究[16-19]。
本文针对下行CoMP系统的单用户功率分配问题,通过把其转换成0-1规划问题,采用DPSO搜索等功率分配的最优解。结果表明本文所提算法逼近理论最优的Jo-WF,在吞吐量和迭代次数上具有显著优势。
1 系统模型
1.1 下行CoMP系统模型
CoMP系统通过多个协同基站(Cooperative Base Stations,CBS)向在小区边缘的用户(User Equipment,UE)提供服务,如图1所示。每个用户向所在的小区基站反馈信道状态信息(Channel State Information,CSI),假设所有基站通过有线方式快速获得瞬时CSI,从而根据各自不同的CSI在相同的频带B上分配功率,同时发送相同的数据。由于CoMP的下行采用OFDMA,不同用户的带宽和总功率分配由用户间的QoS和公平性确定,当各个用户的子载波数和可用功率确定后,多用户资源分配问题就变成如何让单用户获得最大的吞吐量。对于单用户UE一共有K个协同基站为其提供服务,各个协同基站CBSi的功率限制为Pi,i∈ {1,2,…,K}。CBSi和 UE 的信道响应为Hi(f),假设有N个子载波,每个子载波带宽为ΔB=B/N。

图1 3个协同基站同时向小区边缘用户提供服务
由于CoMP的下行采用OFDMA,当小区边缘用户UE分配了N个子载波,有K个协同基站为其提供服务,该用户的吞吐量为各子载波吞吐量之和,则用户吞吐量为

式中:B为用户分配的总带宽;N为子载波总数;Pi,j和Hi,j分别为第i个协同基站CBSi在第j个子载波上的发射功率和信道响应;N0为加性高斯白噪声(AWGN)功率谱。
由于每个CBS的总功率确定,在各个子载波上分配的功率之和等于相应的总功率Pi。因此使用每个子载波分配到的功率比例xi,j来代替绝对功率值Pi,j,即xi,j=Pi,j/Pi。使用 γi,j=(Pi|Hi,j|2)/(N0B/N)来表示当第i个CBS在第j个子载波上分配全部功率Pi时的信噪比。
在各个CBS总功率约束条件下,以小区边缘用户吞吐量最大为目标的功率分配优化问题如下
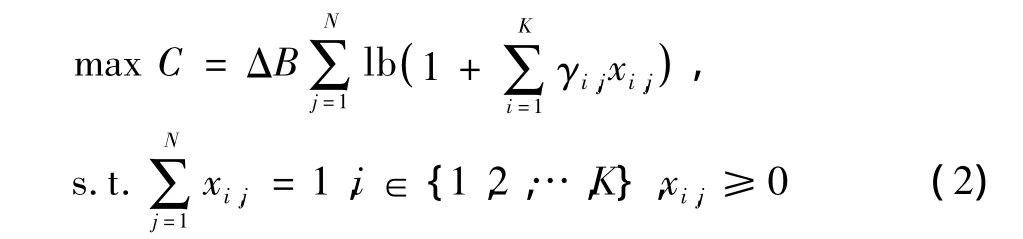
1.2 联合注水功率分配
文献[4]通过分析吞吐量的海森矩阵,证明式(2)最大值在可行域的边界上取得,CoMP最优的功率分配如图2所示。一共有N个子载波要分配功率,只有1个子载波(序号为n)是K个CBS都分配功率的,剩下的子载波被分成K份,分别被各个CBS使用,比如第1个CBS1使用K1个子载波,其他的CBS不在这K1个子载波分配功率;第k个CBSk使用Kk个子载波,其他的CBS不在这Kk个子载波分配功率。
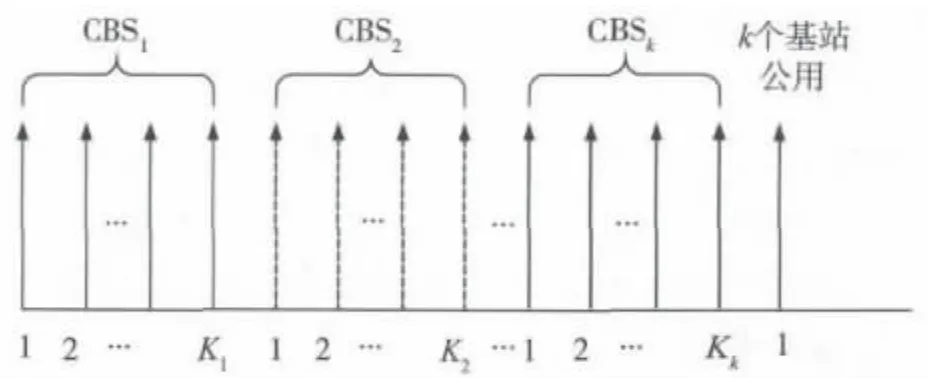
图2 CoMP最优功率分配,子载波排列不分次序
其中,N=K1+K2+...+Kk+1。从而式(2)转变为求解下面的凸优化问题

通过拉格朗日对偶的方法,可以获得各个CBS的注水水位λi为

可以看到λi由各个CBS在公用子载波n上的信噪比 γi,n以及每个 CBS 所使用的子载波 γi,n倒数之和确定。当获得λi后,相应的各个子载波分配的功率比例xi,j为

最优的功率分配如式(6)所示,需要迭代找到每个CBS使用的子载波和公用的n子载波,保证每个P都大于零,即

2 DPSO等功率分配算法(DPSO-EPA)
2.1 经典DPSO算法
离散粒子群算法(DPSO)中针对解决0-1规划问题的BPSO,每个粒子用一个二进制变量来表示,每个取值在{0,1}的粒子在解空间中移动。粒子的速度则用二进制变量的翻转概率来表示,t时刻,种群中第i个粒子的速度和位置更新公式分别为
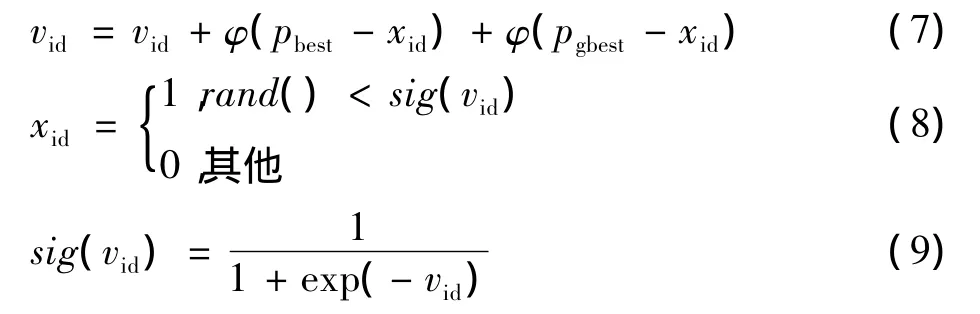
式中:xid和vid分别为种群中第i个粒子的位置和变化率;φ为常数,称为学习因子;pbest和pgbest分别表示种群中第i个粒子找到的的最优位置和全局最优位置。xid,pbest和pgbest都只能是0或1,vid因为表示的是概率,则限制在[0,1]之间。函数sig(vid)是一个转换限制函数,能够保证xid的每一个分量都限制在[0,1],而rand()则表示一个[0,1]之间的随机数。vid值越大,粒子的位置xid选1的概率越大,vid值越小,xid选0的概率则越大。BPSO算法各参数的分析和算法具体步骤见文献[18]。
2.2 DPSO等功率分配算法
联合注水算法需要不断地迭代来获得最优的功率分配。确定每个CBSi对应使用子载波Ki和公用子载波n将非常复杂。并且每当计算出注水水位λi后,如果xi,j<0都需要重新迭代,当可用子载波总数N和CBS数目K增大时,由于需要确定每个CBS分配的子载波数目和公用子载波,迭代次数也会大幅递增。根据文献[5-6]只要分配好子信道,平均功率分配和注水算法的差别将很小,同时为简化系统实现的复杂度,本文考虑使用平均分配功率的算法来逼近最优解。
采用功率平均分配后,将消除式(2)的每个CBSi总功率Pi的约束条件使得易于计算。原先每个子载波的各个不相同的功率比率xi,j,简化成该子载波分配或者不分配功率两种情况,用ri,j∈{0,1}表示。xi,j由ri,j的总和来确定。这样原先的连续凸优化问题转变为确定ri,j的0-1规划问题。从而下行CoMP的功率分配优化问题可描述为

传统求解0-1规划问题有枚举法、分支定界法和动态规划法等,但当问题规模扩大时,其计算量呈指数级增加。大量快速算法被提出,比如遗传算法、模拟退火算法、粒子群算法等。相对遗传算法DPSO简单容易实现并且没有太多参数需要调整,尤其在问题的维数增加时,DPSO算法比遗传算法速度快[18-19]。本文采用DPSO来逼近最优解,以式(10)为适应度函数。
3 实验结果及分析
通过蒙特-卡罗来分析各种功率算法的性能。取1 000次独立的频率选择性衰落信道下,各个不同功率分配算法下的用户吞吐量的平均值,信道由6路随机瑞利多径组成。假定下行CoMP在每个子信道的噪声N0ΔB都相同为-105 dBm。其他具体参数参见表1[2]。
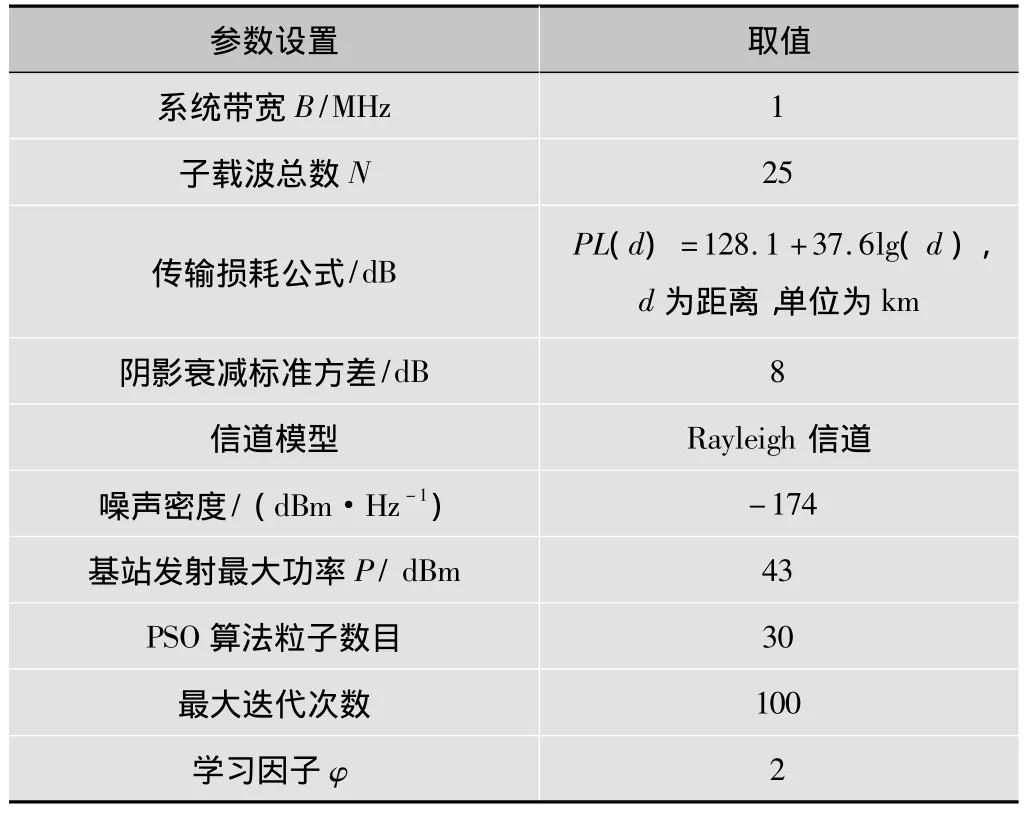
表1 仿真参数
3.1 DPSO-EPA算法性能比较
仿真选择K个CBS进行仿真,每个CBS的发射功率限制都一样为P,其中一个CBS与用户的距离d为1.0 km,其他CBS的距离d为0.6 km。当K=2时,d1=1.0,d2=0.6;K=3 时,d1=1.0,d2=d3=0.6;K=4 时,d1=1.0,d2=d3=d4=0.6。
选取文献[4]中的联合注水算法(Jo-WF),传统分立注水算法(SP-WF)和本文提出的DPSO-EPA进行吞吐量的比较,仿真结果如图3所示。图4给出了当P=40 dBm,K=2时3种算法的吞吐量细节图。表2给出在不同发射功率限制下的DPSO-EPA,SP-WF分别和Jo-WF吞吐量的相对误差。

图3 不同发射功率P下用户的吞吐量

图4 当P=40 dBm,K=2时的用户吞吐量

表2 算法相对吞吐量比较
由仿真结果可以看到,DPSO-EPA算法的吞吐量逼近理论最优的Jo-WF,且随着发射功率和CBS数目K的增加,其差别逐渐变小。当两个CBS同时工作,发射功率为40 dBm时,差别只有0.8%。DPSO-EPA算法在发射功率较高时优于SP-WF,这是因为SP-WF没有利用联合信道的信息,所以SP-WF得到的功率分配算法仅仅是局部最优;当发射功率较低时,由于使用等功率分配没有利用不同信噪比子载波的分集效应,故低于传统注水。
3.2 DPSO-EPA算法收敛速度
图5给出不同CBS数目K下的DPSO-EPA算法和Jo-WF吞吐量的相对误差随迭代次数变化的曲线。结果表明,相对误差在迭代开始迅速减少,接下来经过几次迭代搜索,结果收敛。同时由于K的增加,算法需要搜索的空间也相应增大,所以K=4结果收敛需要100次迭代,而K=2只需要40次。因此随着更多的子载波数和CBS数可用时,DPSO-EPA算法需要更多的粒子数目和迭代次数。
4 小结
本文针对下行CoMP系统的单用户功率分配问题,通过把其转换成0-1规划问题,提出了采用离散粒子群优化的等功率分配算法(DPSO-EPA),其吞吐量性能与联合注水算法基本相当,运算量小,复杂度低,易实际使用。本文中暂时没有考虑比特加载,下一步将结合自适应调制技术,在功率分配好的基础上,形成完整的CoMP系统资源分配算法。
:
[1]ETRI.3GPP 36.819 V11.1.0,Technical specification group radio access network:coordinated multi- point operation for LTE physical layer aspects(Release 11)[S].2011.
[2]ETRI.3GPP 36.814 V9.0.0,Further advancements for E-UTRA physical layer aspects[S].2010.
[3]PISCHELLA M,BELFIORE J C.Distributed resource allocation for rate constrained users in multi-cell OFDMA networks[J].IEEE Commu.Letters,2008 ,12(4):250-252.
[4]LUO B,CUI Q M,WANG H,et al.Optimal joint water-filling for OFDM systems with multiple cooperative power sources[C]//Proc.IEEE Global Telecommunications Conference.Miami:IEEE Press,2010:1-5.
[5]CHOW P S.Bandwidth optimized digital transmission techniques for spectrally shaped channels with impulse noise[D].Stanford,CA:Stanford Univ.,1993.
[6]VISWANATH P,ANANTHARAM V.Asymptotically optimal water-filling in vector multiple-access channels[J].IEEE Trans.Inf.Theory,2001,47(1):241-267.
[7]LUO B,CUI Q M,TAO X F.Constant-power joint-waterfilling for coordinated transmission[C]//Proc.IEEE Global Telecommunications Conference.Houston:IEEE Press,2011:1-6.
[8]张晓亮,纪红.多蜂窝系统下行多用户CoMP中一种次优的子载波和功率分配算法[J].北京邮电大学学报,2012,35(4):1-5.
[9]黄晓燕,毛玉明,吴凡,等.中继增强的无线蜂窝多小区系统的联合调度与功率控制算法[J].电子与信息学报,2012,34(7):1665-1671.
[10]戴翠琴,钟声.CoMP系统中的天线选择和功率分配联合算法[J].重庆邮电大学学报:自然科学版,2013,25(1):90-95.
[11]WANG Da,XU Xiaodong,CHEN Xin,et al.Joint scheduling and resource allocation based on genetic algorithm for coordinated multi-point transmission using adaptive modulation[C]//Proc.IEEE Int.Symp.Personal.Indoor.Mobile Radio Commun.Sydney:IEEE Press,2012:220-225.
[12]朱国晖,李佳蔚,赵季红.LTE-A系统中基于CoMP的下行跨层功率分配优化方法[J].计算机工程与设计,2012,33(10):3702-3707.
[13]EBERHART R C,KENNEDY J.A new optimizer using particles swarm theory[C]//Proc.the Sixth International Symposium on Micro Machine and Human Science.Nagoya:IEEE Press,1995:39-43.
[14]KENNEDY J,EBERHART R C.A discrete binary version of the particle swarm algorithm[C]//Proc.IEEE International Conference on Systems,Man and Cybernetics.Orlando:IEEE Press,1997:4104-4108.
[15]汪禹喆,雷英杰,周林,等.直觉模糊离散粒子群算法[J].控制与决策,2012,27(11):1735-1739.
[16]黄平.粒子群算法改进及其在电力系统的应用[D].广州:华南理工大学,2012.
[17]邓伟林,胡桂武.一种求旅行商问题的离散粒子群算法[J].计算机与现代化,2012(3):1-4.
[18]郭文忠,陈国龙,陈振.离散粒子群优化算法研究综述[J].福州大学学报,2011,39(5):631-638.
[19]杨维,李岐强.粒子群优化算法综述[J].中国工程科学,2004,6(5):87-93.

