基于完美信息博弈的多无线电信道分配算法
戴昊峰,何世彪,2,韩 辉,张 晖,2,谭 冕
(1.重庆通信学院重庆 400035;2.重庆大学通信学院重庆 400044)
无线ad hoc网络采用分布式、自组织、无中心的架构,可以很方便地应用于不同场合,但是在网络资源(主要是频谱资源)有限的情况下,如何有效、公平地配置网络资源,是ad hoc网络在运用时遇到的一个最为关键的问题,也是目前尚未完全解决的问题[1]。近期的研究表明,博弈论可以作为此类问题的有效分析工具[2-3]。根据用户对网络信息的掌握情况,可分为完美信息博弈和不完美信息博弈。所谓完美信息博弈是指参与者知道用户冲突域内每个设备所使用的信道,或者每个信道所分配的无线电。随着无线射频收发器硬件相关技术的迅速发展:一是无线网络节点的射频端已经具备感知周围信息的功能,二是在一个无线网络节点上装备多个射频器前端已经成为广泛的选择。因此选择基于完美信息博弈的多无线电信道分配在ad hoc网络中具有可行性,在未来也有很大的发展前景,对它的研究有着重大的意义[4-5]。
目前,对于无线ad hoc网络的信道分配机制主要分为集中式和分布式两种,本文主要研究了分布式的信道分配机制。文献[6]提出了一种最优信道带宽调制方法,利用一种“装箱压缩”方法并结合多无线电技术提出分布式流量感知的信道带宽调制算法,有效地提高了频谱使用率,但没有考虑用户获取信道的公平性;文献[7]中采用一种对每个节点分配同样信道集合的方式,这种信道分配方式虽然易于实现,也能够保证网络的连通性,但不足以适应复杂的网络情况;文献[8]中根据用户获取信息的不同提出了3种算法解决多无线电信道的分配问题,3种算法都从不同方向实现了自私节点向纳什均衡点的收敛,并通过理论证明和仿真结果验证了第三种信道分配算法可以实现在网络中达到纳什均衡的目的,但该算法假设网络场景为单冲突域,无法适应多冲突域的网络场景。文献[9]在文献[8]的基础上提出了适合网络场景为多冲突域的算法,算法假设两跳范围的用户为冲突域内,并以此为网络中的各个自私节点以非合作博弈的方式对其无线电接口分配信道,最后仿真对比了单多冲突域的用户平均传输速率,证明多冲突域情况更能最大化信道利用率,但是该算法复杂度较高,不易实现。针对以上算法的不足,本文提出一种较低复杂度的信道分配算法,用户通过感知自身冲突域内其他用户的信道信息来选择信道以达到纳什均衡分配所需满足的条件(即使效用函数最大),仿真结果表明算法可以达到纳什均衡点,并能够较好地改善网络性能(与单冲突域情况对比)。
1 系统模型
本文假设使用频分复用(Frequency Division Multiple Access,FDMA)技术,将可用频率分为相同带宽的正交信道(在IEEE802.11a协议中有8条信道)。定义可用正交信道集合为C,可表示为



图1 网络拓扑结构
假设距离用户两跳及以内的用户为冲突域内用户,用户可以感知自身冲突域内用户的信道信息。如图1所示,用户1的冲突域包含用户2,3,9,10,即用户1在信道分配时可以感知到上述用户的完全信息。其他范围为用户1的冲突域外,此时假如用户6使用与用户1相同的信道则不会对用户1产生干扰。
由于使用多无线电技术,用户能够同时使用多个信道进行数据的传输,那么用表示用户i的冲突域内用户i使用信道c∈Ci的无线电数目,Ci为用户i使用的信道集合,有Ci⊂C,且该用户所占用的所有无线电数目为,相应的,用户i的冲突域内使用信道c的无线电数目为。基于以上假设,用户i的信道分配策略可以表示为:,其中。从表示式可以看出,策略向量就是占用每个信道的用户无线电数目,那么所有用户的策略矩阵S可以表示为

式中:用S-i表示除用户i外所有用户的策略集合。
用户i的用户收益,即用户所占用信道的带宽(用户传输速率)表示为Ui,由于用户位于不同的冲突域,假如用户j位于用户i的冲突域内,用户j的无线电如果占用的信道为用户i的无线电所占用的,那么它们将平分该信道总的带宽,假设信道的带宽不会因为无线电数目的增加而下降[9],而对于用户i冲突域外的用户而言,使用相同的信道将不会对用户i造成干扰。因此如果用户i的无线电占用信道c,那么用户i的无线电能获得的带宽为

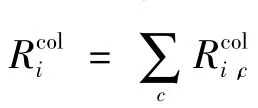
2 多无线电信道分配策略的纳什均衡
本节研究在多冲突域条件下博弈的纳什均衡存在性的判定条件。首先引入纳什均衡[2]的定义:


换句话说,在一个已经达到纳什均衡的策略中,没有用户能够通过单方面地改变用户策略来改变用户的收益。然而,纳什均衡解可能存在两种情况,一种是可能存在多个纳什均衡解,二是纳什均衡的解从系统模型来看不一定是最优的。由此引出了帕累托最优[2]的概念:
定义2:帕累托最优(Pareto-Optimality)策略向量Spo是帕累托最优的,假如存在S'使得式(5)成立
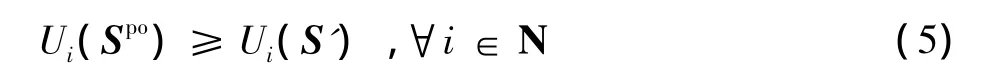
换句话说,假如一个策略集合是帕累托最优的,那么不存在其他策略集合s'使得至少有一个参与者的效用得到增加,而其他参与者的效用不会减少。
引理1:如果S*是一个多无线电多信道分配博弈的纳什均衡策略,那么就有ki=k,∀i成立。
引理1表明,一个理性用户会使用所有无线电来增加自身的效用。
根据文献[8]和[9]有以下定理成立,此定理有较强的适应性,无论是在单冲突域还是多冲突域环境中都能成立,接下来本文所提算法将紧密围绕这个定理展开。


定理1:信道分配策略S*是一个NE的,当且仅当满足以下两个条件:

由文献[9]还可知假如信道c的带宽函数R(kc)独立于kc,∀c∈C,那么NE信道分配策略S*一定是帕累托最优的。也就是假如R(kc)的值不会随着kc的变化而变化,那么得到的NE信道分配策略一定是最优的。因此本文都假设R(kc)是独立于kc。
3 信道分配算法描述
基于完美信息的信道分配算法要求用户在信道分配前不仅知道自身的无线电所使用的信道情况,还要求用户节点的无线电射频端感知自身冲突域内其他用户的信息,以此来确定自身的信道策略使整体策略满足定理1中的条件(使用户自身效用函数达到最大值)。
算法最初进行一次随机信道分配,分配完成后,每个用户感知自身冲突域内每条信道c∈C上的无线电数目,并试图通过重新组织分配信道给用户的无线电接口来增大用户总的传输速率。但是这个过程可能会出现一个问题:很多用户同时申请改变信道,这将会造成冲突,影响算法效率,延长收敛时间。为此,本文将引入IEEE802.11的退避机制来解决这个问题,首先定义一个退避窗口W,并且每个用户以相同的概率从集合{1,2,…,W}中随机选择一个初始值作为退避计数器的值。然后在每一轮每个用户都会将自身退避计数器值减1,当退避计数器的值为0时用户才能重新将信道分配给无线电,在用户分配完信道后,又返回退避窗口W重置一个随机值。这样有效地避免了用户间的冲突,增强了网络整体性能。当用户的改变顺序确定后,此时如果轮到用户i∈N改变其信道,那么用户i首先感知其冲突域内有哪些用户和其所有信道信息,将用户i冲突域内用户记为,它是从所有用户中提取出来的部分用户的集合,记为用户集合中使用次数最少的信道,表示用户ii的无线电使用信道的数目,为用户i的冲突域内用户使用信道的无线电数目,同理为为用户i的冲突域内用户使用信道b的无线电数目。当完成第一部分信道分配后此时用户i的冲突域内用户已经满足定理1中第2个条件,但算法不一定满足第1个条件,所以需要再次判断分配。最后经过多次循环可以达到整体的纳什均衡点。
算法的流程图如图2所示。

图2 算法流程图
4 仿真分析
为了验证上述算法的相关性能,本小节设计了如下的仿真场景。用户的拓扑结构如图1所示,假设每条信道的吞吐量假设固定均为R(kc)=54 Mbit/s,由前文可知其不随着无线电数目的增加而下降。退避窗口值W=20,编程语言为MATLAB。
图3给出一个已达纳什均衡点的信道分配结果,其中,用户数目=10,每个用户的无线电接口数目相同为k=3,正交信道数目为=8,从图中可以看出,任何用户在其冲突域内的信道分配结果都满足定理1的条件,达到了纳什均衡。
图4中用户数目=10,每个用户的无线电接口数目k=3,正交信道数目为=8,但是假设所有用户在同一冲突域内,并假设距离用户两跳及以内的用户为冲突域内用户,即用户位于不同的冲突域中,图示呈现了用户在单冲突域和多冲突域中用户收益的仿真对比,可以看出,用户在多冲突域中具有更高的信道使用率。

图3 一种纳什均衡的信道分配结果

图4 用户在单多冲突域收益对比
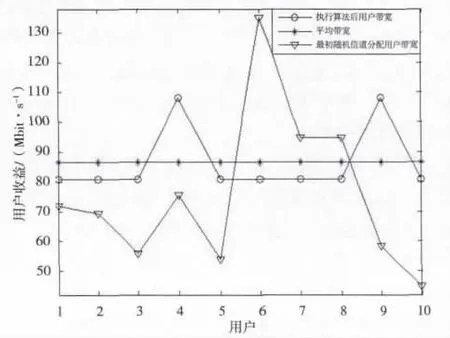
图5 算法执行前后用户收益的对比
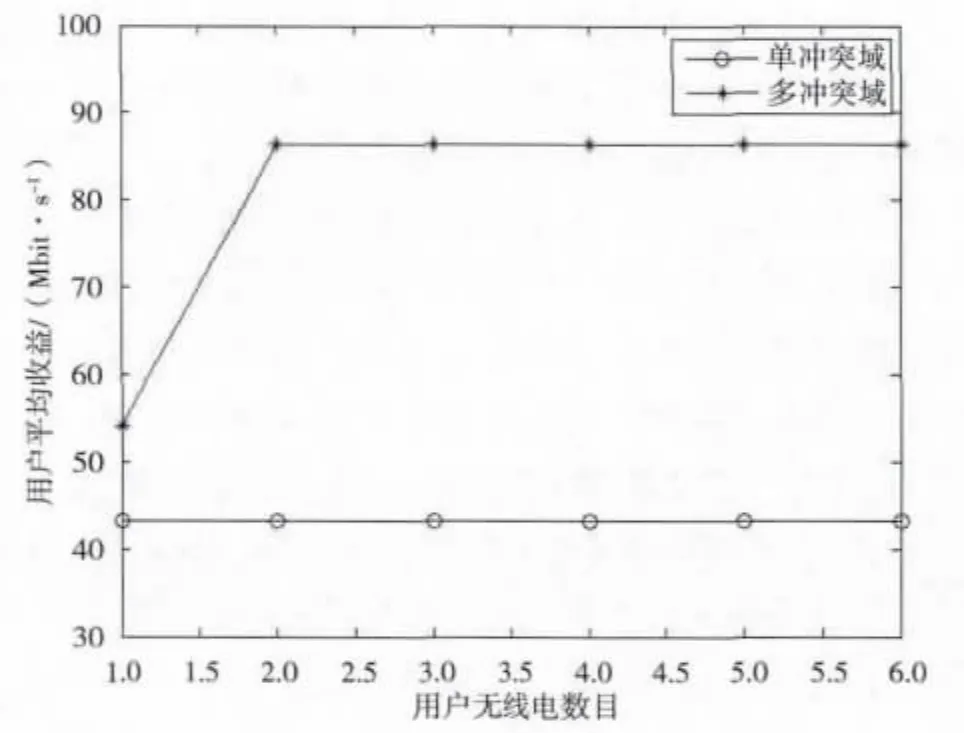
图6 不同的无线电数目对用户收益的影响
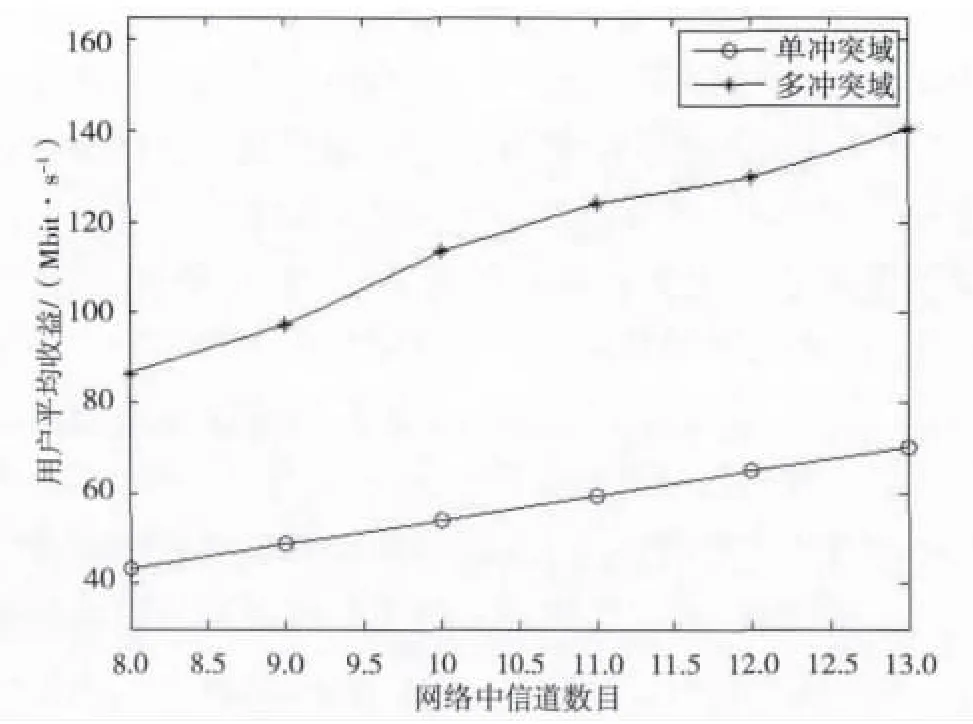
图7 不同信道数目对用户收益的影响
5 结束语
众所周知,无线ad hoc网络的信道分配问题一直都是一个NP难问题,本文根据无线ad hoc网络分布式的特点,引入博弈论的方法,提出了一种适用于多冲突域情况的完美信息信道分配算法,通过实验仿真与单冲突域的情况做出对比,验证了本文的算法可以更好地最大化信道的使用率,使网络负载更加均衡。本文考虑的是完美信息,实际中由于硬件条件等达不到要求可能很难做到获取完美信息,并且文中并没有考虑多冲突域环境下可能存在的隐藏/暴露终端等问题,因此下一步工作将考虑如果无法获取完美信息应该如何达到纳什均衡并且兼顾隐藏/暴露终端问题。
:
[1]汪涛.无线网络技术导论[M].北京:清华大学出版,2009.
[2]SRIVASTAVA V,NEEL J O,MACKENZIE A B,et al.Using game theory to analyze wireless ad hoc networks[J].IEEE Communications Surveys and Tutorials,2005,7(1/4):46-56.
[3]彭文艺,饶志强,吴涛.博弈论在无线自组网技术中的应用[J].计算机与数字工程,2006,34(6):117-119.
[4]BAHL V,ADYA A,PADHYE J,et al.Reconsidering the wireless LAN platform with multiple radios[C]//Proc.Workshop on Future Directions in Network Architecture.[S.l.]:IEEE Press,2003.
[5]YANG D,FANG X,XUE G.Channel allocation in non-cooperative multi-radio multi-channel wireless networks[C]//Proc.IEEE INFOCOM.Orlando,FL:IEEE Press,2012:882-890.
[6]RANIWALA A,CHIUEH T.Architecture and algorithms for an IEEE 802.11-based multi-channel wireless mesh network[C]//Proc.24th Annual Joint Conference of the IEEE Computer and Communications Societies.New York:IEEE Press,2005:2223-2234.
[7]DRAVES R,PADHYE J,ZILL B.Routing in multi-radio,multi-hop wireless mesh networks[C]//Proc.10th Annual International Conference on Mobile Computing and Networking.[S.l.]:ACM Press,2004:114-128.
[8]FELEGYHAZI M,CAGALJ M,BIDOKHTI S S,et al.Non-cooperative multi-radio channel allocation in wireless networks[C]//Proc.26th IEEE International Conference on Computer Communications.[S.l.]:IEEE Press,2007:1442-1450.
[9]KIM H K,LEE T J.CHASS-M:channel assignment for fair payoff based on game theory for wireless multi-hop networks[C]//Proc.4th International Conference on Innovations in Information Technology.Dubai:IEEE Press,2007:282-286.
[10]史佳佳,刘宴兵.多射频无线网络中多信道分配方法的研究[J].计算机应用研究,2012,29(6):2290-229.
[11]郑鹏宇,何世彪,戴昊峰,等.基于最大化网络吞吐量的WMN信道分配算法[J].电视技术,2013,37(19):176-180.

