离石黄土渗透规律试验研究

王建斌

(西北大学地质学系/大陆动力学国家重点实验室，陕西西安710069)

水在工程界被称为“万恶之源”，在滑坡领域更是有“无水不滑”之说。在我国离石黄土广布的西北地区，因强降雨、冰雪融化、农田漫灌而引发的滑坡、泥石流等灾害造成重大人员伤亡。这些灾害的发生，与降雨关系密切已早为人知，但人们对这种关系的认识和理解仍不够深入。为此，有必要对降水在非饱和离石黄土中的作用过程、作用方式方面进行深入研究。众多学者对类似问题开展过研究。Horton R E[1]最早提出了稳定入渗率的概念;Philip[2]认为降水在入渗过程中任意时刻的入渗率与实践呈幂级数关系，并初步建立了入渗模型;孙菽芬[3]根据柱塞流假设，推导了决定入渗率等于雨率时的时间及该时的湿润封面位置。魏忠义[4]对河沟流域各类型下垫面水分入渗规律及特征进行了系统研究，结果表明Kostiakov公式以及Horton公式较符合河沟流域的实际入渗情况。王文焰[5]对Green－Ampt入渗模型进行了改进，推导出了适用于黄土地区的积水入渗模型，与实际吻合较好。李亚娟[6]通过野外积水入渗试验，对不同地貌特征与不同土地利用条件下土壤入渗的变化规律进行了研究，结果表明塬面和阴坡较符合Kostiakov入渗率均表现为阴坡大于阳坡。

非饱和土渗透特性研究方面取得了长足发展，但对于离石黄土在不同降雨强度下，水在土体中入渗的变化规律的研究尚空缺。为此，本文通过构建多种降雨试验模式，探讨不同雨强(15 mm、50 mm、70 mm)时湿润峰值位置随时间的变化规律，利用数学方法分析预测可能的最深湿润峰值位置、稳定富集速率等，为黄土坡地地质灾害致灾机理及防治研究提供借鉴。

1 试验原理

水流的运动同样符合运动学规律，即

式中H表示入渗深度，V表示入渗速度，t表示入渗时间。若知某时刻tn入渗峰值面的位置Hn，则可在直角坐标中记录点Mn(tn，Hn)，同理，通过记录不同时刻入渗峰值面的位置，可得出一系列点M1，M2，…，Mn，利用这些点可绘制出入渗峰值面位置(入渗高度)H与时间t的关系曲线。

假设入渗高度H与时间t呈二元非线性函数关系，即

式中a，b，c均为常数。某时刻tn水流的渗透速率Vn等于该点的导数H'n，通过求函数关系式的导数可得出该点的渗透速率，即

2 试验系统

基于上述原理和思路，初步探索出了一套能够测试水在非饱和土体中入渗、径流、富集等参数的试验系统[7]，如图1所示。

该装置可划分为4个部分，具体包括:

1)降雨部分。由供水箱、控水开关、导水管、LZB型流量计和喷头等部件组成。供水箱通过导水管导出，LZB型流量计可通过微调开关控制所需流量大小，用以模拟不同降雨的强度;

2)渗流(取样)装置。包括PC透明塑料圆筒、钢尺和透水石。PC透明塑料圆筒作为试验筒，利用类似环刀法，将原状离石黄土取入PC透明圆筒，钢尺用以读取入渗深度(峰值位置)，可以获得入渗深度与时间的相关参数。为确保降雨能以面状均匀入渗，试样顶部放置一块透水石;

3)径流部分。由量筒、导管、凡士林等组成，试样筒侧壁留有小孔，位置与透水石顶面齐平，与导管相连至量筒内;

4)富集部分。主要包括漏斗、烧杯以及铁丝网、纱布构成的反滤层。土样底部渗出的水通过反滤层，由漏斗进入烧杯，可以获得富集量与时间的相关参数。

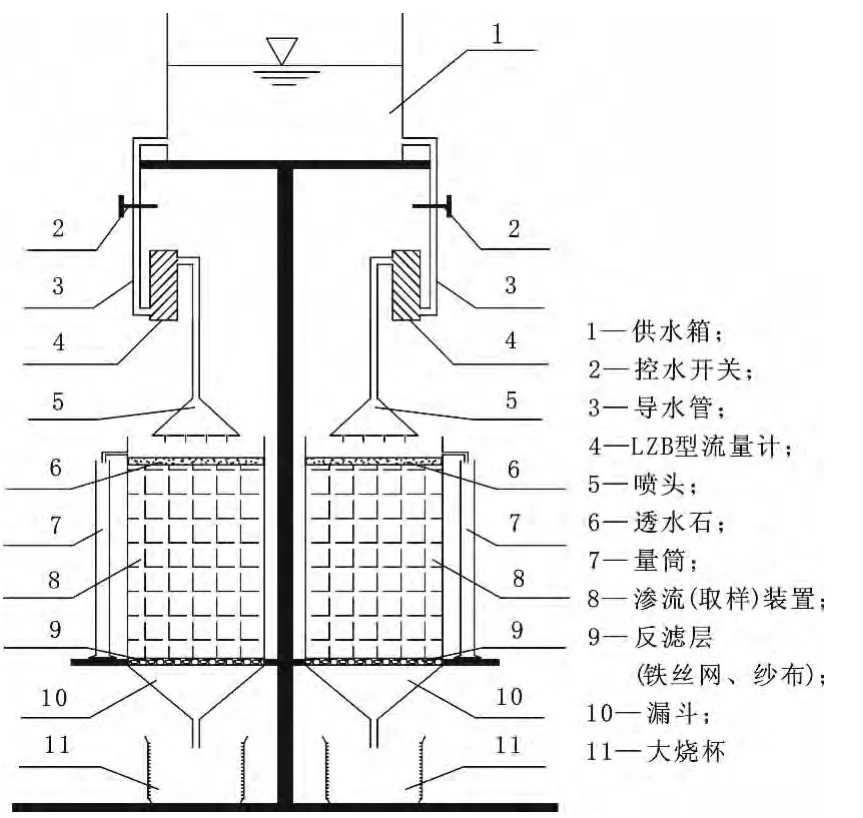
图1 渗透试验系统设计图

3 试验方案

利用上述试验系统，对不同雨强时湿润峰值位置、富集量等参数随时间的变化规律进行研究。考虑到小雨所需时间过长，加之小雨诱发灾害的可能性较小，笔者设计了三种不同强度的降雨，如表1所示。

表1 模拟降雨量等级参数

利用取样器取原状离石黄土3组(6个)，取样点为陕西省子长县安定镇，该地区地处陕北黄土高原，黄土覆盖厚度大，面积广，该区离石黄土颜色比较深，呈红褐色，垂直节理发育，组织较疏松，易被揉碎，具有典型代表性，以此区土样为研究对象能够代表大部分离石黄土。室内试验测得试样的基本物性指标如表2所示。

表2 土样基本物性指标

将上述试样安装在试验系统上，调节流量计微调开关至设定值开始试验，每隔一定时间测读入渗峰值的位置。当入渗峰值到达底部时，富集装置开始发挥作用，读取不同时刻烧杯中的积水值，即为富集量。一段时间后，当漏斗中的滴水匀速下落时，达到稳定富集状态，试验终止。

4 结果分析

4.1 入渗规律

图2为离石黄土入渗锋面时态曲线，t=10min时，雨强为15 mm时，下渗深度小于10 mm;雨强为50 mm时，下渗深度为28 mm;雨强为70 mm时，下渗深度为50 mm，说明雨强入渗速率与雨强呈正相关，即同一时刻雨强越大，入渗锋面位置越低。当下渗深度均达到60 mm时，雨强15 mm用时27 min，雨强50 mm用时26 min，雨强70 mm则用时10 min，说明对于同样的渗透深度，雨强越大，历时越短。对于第一个拐点用时，雨强越大，历时越短。

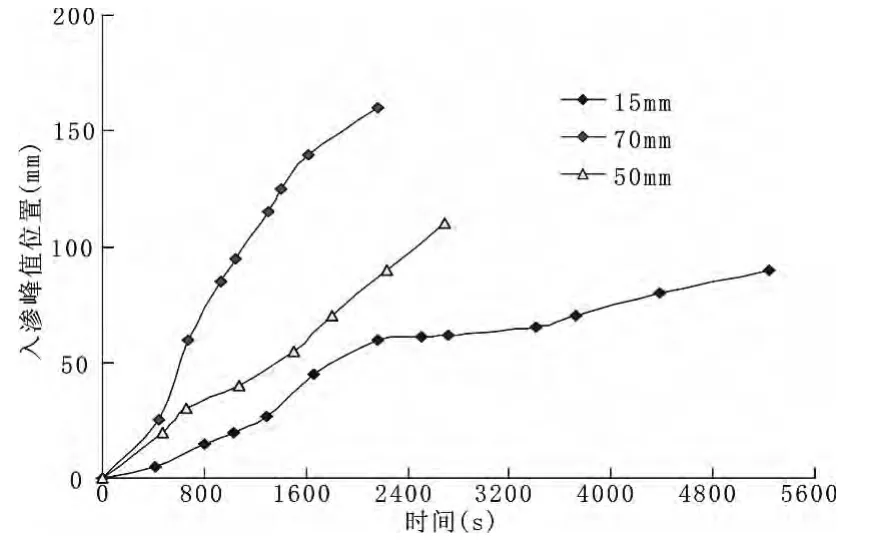
图2 离石黄土入渗锋面时态曲线

图3为离石黄土入渗速率时态曲线，随着时间的持续，入渗速率整体是呈减小的趋势的。0～15 min时，渗透速率迅速增长且15 min时增长至最大值，这是由于土样含水率较低，黄土具松散、垂直节理发育及大孔隙等性质，为雨水的入渗提供了良好的先决条件。15 min～20 min时，渗透速率呈减小趋势，这是由于随着含水量的增大，黄土中的部分结合水转变成自由水，土体被压密，在土体中形成了一层粘土壳，具一定的隔水性，阻碍的水的入渗，从图2可以看出达到第一个拐点。随着降水量的增加，土体由非饱和状态逐渐过渡为饱和状态，土体不再吸收水分而直接下渗至粘土壳，粘土壳由于不能承受上部土、水的共同重量而破坏，粘土壳的阻碍作用减弱，降水继续下渗，入渗速率最终趋于稳定。比较不同雨强可知，雨强越大入渗速率越大，这说明长持时大暴雨是产生滑坡灾害的重要因素。

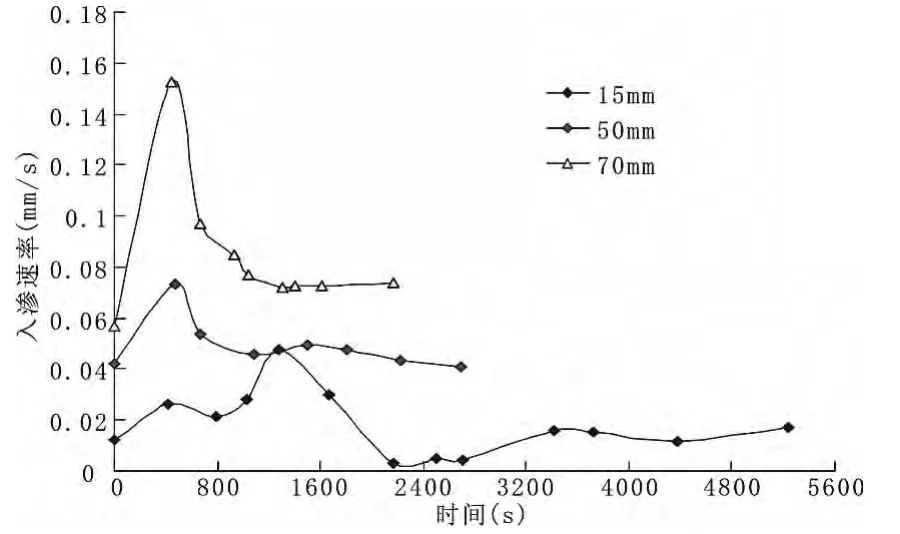
图3 离石黄土入渗速率时态曲线

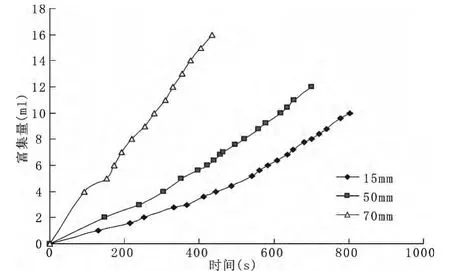
图4 离石黄土富集量时态曲线

4.2 富集规律

随着时间的持续，由于土体介质的差异性，当降水渗透整个离石黄土层至相对隔水层时便会富集，这是降雨型滑坡产生的主导因素。图4为离石黄土累积富集量时态曲线，前期曲线出现一定的波动，这是由于前期土样底部并未完全饱和，部分降水被土样吸收，随着时间的持续，最终呈标准线性曲线，达到稳定富集状态。达到稳定富集的时间与雨强呈负相关，即随着雨强等级的增加，达到稳定富集历时越短。

图5为离石黄土富集速率时态曲线，前期曲线据一定的波动性，后期与水平轴趋于平行，达到稳定富集状态。稳定富集速率与雨强等级呈正相关，即雨强等级越高，稳定富集速率越大。最终得出雨强分别为15 mm、50 mm、70 mm时的稳定富集速率分别为 0.014 ml/s、0.017 ml/s、0.035ml/s。

图5 离石黄土富集速率时态曲线

5 结论

基于黄土坡地地质灾害的认识，结合运动学理论与方法，设计了一套简易试验装置，对水在非饱和离石黄土中的入渗、富集规律进行了初步探讨，得出了如下结论:

(1)试验装置包括降雨、渗流、富集、径流等部分，具有简单、灵活、操作方便、精度高等特点，可用于模拟大气降水、灌溉水径流、下渗、富集的整个渗透过程;

(2)进行了雨强分别为15 mm、50 mm、70 mm时的非饱和离石黄土降雨入渗模拟试验，得出了一系列入渗(速率)、富集(速率)时态曲线。同一时刻，雨强等级越高，离石黄土的下渗深度越深，同一入渗深度，雨强等级越高，历时越短，雨强等级越高，平均入渗速率越大。不同雨强等级最终均达到稳定富集状态，稳定富集速率与雨强等级呈正相关，最终得出雨强分别为15 mm、50 mm、70 mm时的稳定富集速率分别为0.014 ml/s、0.017 ml/s、0.035 ml/s。

(3)非饱和离石黄土入渗过程是十分复杂的，影响因素亦十分多样，本研究仅是初步的，试验系统有待于进一步完善，但对于黄土坡地地质灾害致灾机理的研究提供了一种新思路、新途径，具有一定的启示意义。

[1]雷志栋，杨诗秀，谢森传.土壤水动力学[M].北京:清华大学出版社，1988.

[2]Philip J R.The theory of infiltration l:the infiltration equation and its solution[J].Soil Sci，1957，83(5):345 － 357.

[3]孙菽芬.降雨条件下土壤入渗的规律研究[J].土壤学报，1998，25(2):119－124.

[4]魏忠义，王治国，王春红，等.河沟流域水分入渗的数学模型[J].山西农业大学学报，2000，(01):59 －63.

[5]王文焰，汪志荣，王全九，等.黄土中Green－Ampt入渗模型的改进与验证[J].水力学报，2003，(05):30－34

[6]李亚娟，宋孝玉，李怀有，等.甘肃西峰南小河沟流域土壤入渗分布规律研究[J].西北农林科技大学学报(自然科学版)，2006，34(12):148－151.

[7]王念秦，刘晓玲，王建斌.非饱和土直渗仪的研制与应用[J].工程地质学报，2012，20(5):796－799.