体育综合评价中指标权重确定的理论与实践

沈梦英 赵书祥

(1. 河南科技大学，洛阳 471023;2. 北京体育大学体育统计与测量教研室，北京 100084)

1 前言

如何科学的评价体育应用领域中各种体育实践活动是进一步推动国家体育运动健康发展的保障和基础(赵书祥，2008)[1]。有研究者也认为体育活动的影响及效果是一个高度综合概括的评价范畴，因此无法用一句话或一个指标来表达清楚，必须通过在指标体系中选择一系列有代表性的评价指标从各个侧面反映，才能近似表达其影响效果(祁国鹰，徐明，2006)[2]。因此对体育活动的效果和影响因素进行评价时，采用综合评价的方法也是必然的。

近年来在体育领域中综合评价的方法得到了广泛的应用，积累了很多的研究成果，但也存在很多问题。徐明欣，高斌，李瑞年，鞠传进(2000)[3]从层次分析法的方法过程入手，重点介绍了“体育课程评估”和“体育教学质量评价”中构建评估指标体系和求解权重的方法步骤。任弘(2004)[4]在体质研究中人体适应能力的理论与实证研究中运用因子分析法确定了人体适应能力各指标的权重。祁国鹰，徐明(2006)[2]在体育统计简明教程中介绍了专家调查法确定权重的理论与方法。赵书祥(2007)[5]的研究重点阐述了层次分析法的应用。方强(2010)[6]采用主要采用层次分析法和问卷调查法对高等学校体育教学质量评价体系进行了研究。于万清(2010)[7]运用层次分析法对阳光体育背景下学生体育成绩进行了量化评定。赵书祥(2008)[1]通过文献资料法对国内近二十年来关于体育领域综合评价的研究进行了分析，研究显示目前国内体育综合评价应用研究中存在的主要问题之一就是体育综合评价研究中权重的计算方法也有误用现象。以上前人的研究中大多是仅涉及到综合评价中的一种权重(也称加权，它表示对某指标的重要性程度进行定量分配)的确定方法，如因子分析，层次分析法等。

综合评价的重要工作之一就是建立评价指标体系。评价指标体系是实现对评价对象识别的依据，其科学性是评价结果真实可靠的保证。因此要从研究目的出发，穷尽所有的可能因素，建立初选的指标体系，再经过科学的论证建立起综合评价的指标体系，在此基础上确定各指标的权重。体育科学研究中许多研究者面对众多的权重赋值方法时不知如何选择。针对此问题，有必要将一些综合评价中涉及的权重系数的问题给与详细阐述，并加以区分，以期对体育科研中指标体系综合评价工作提供理论指导。本研究目的是总结体育科研综合评价常用权重的确定方法，并结合实践将每种方法的适用条件和操作程序分别进行阐述。本研究将重点介绍利用专家调查法、因子分析法、层次分析法三种常用的体育综合评价中确定指标权重的方法。

2 研究方法

通过前人研究进行梳理并采用实例演示的方法，对体育科研中常用综合指标权重确定的方法如专家调查法、因子分析法、层次分析法等的适用条件、操作过程与方法进行总结与演示。

3 研究结果

3.1 专家调查法确定权重

3.1.1 适用条件

专家调查法实际上是一种经验确定指标体系和各指标权重的方法，根据相关研究领域的权威专家主观认为的重要性程度赋予相应的权重，即主观确定权重的方法。专家组的成员一般由15人左右组成为宜，问卷发放量和专家人数一致。

首先通过查阅文献及专家访谈等方法，建立某个考核评价体系的初选指标；然后针对初选指标对专家进行访谈及问卷调查，确定入选指标体系。评价指标确定后，后续的工作就是确定各个评价指标的权重系数。本研究就是在指标已经确定的基础上，采用专家调查法确定出各个指标的权重系数。

3.1.2 专家调查法确定指标权重的过程与方法

由于各个评价指标在整个考核评价中所处的地位和重要性不同，要根据其重要性和具体条件合理性确定各个指标的权重系数。首先选出精通于某研究领域的权威专家，组成专家组。让专家们按照其认为的各个指标的相对重要程度打分。打分的级数可以是0到10分共十一级，也可以是1到5分共5级。一般情况下我们运用0到10级的打分办法，给专家更大的选择空间，以便充分的发表意见。专家调查表如表1。

表1 专家调查中指标赋值情况

最后将专家组的打分信息进行汇总(见表2)，以用来确定出每个指标的权重系数。有的研究还需要最后建立起相应的考核评价标准。

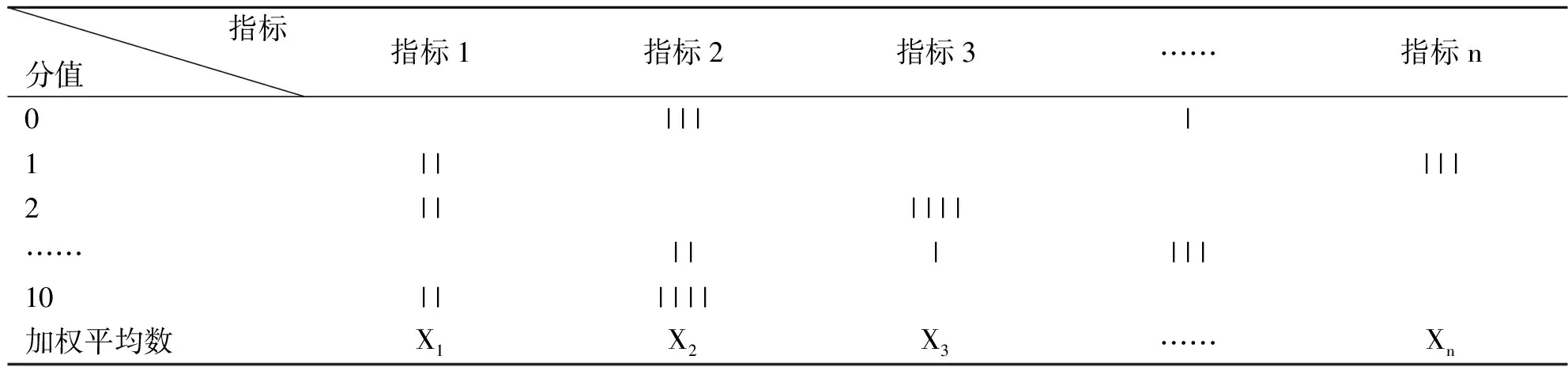
表2 专家调查资料汇总

注：“|”代表针对某指标所有专家选中某一分值的频数为1次。

3.1.3 应用举例

某项研究需要对篮球教练员的执教能力进行综合评价。一级指标有5个，分别是比赛成绩、职业道德、训练水平、合作关系及参赛能力。再如比赛成绩的二级指标分别是最终成绩、阶段性大赛成绩、训练成绩。研究共发放专家调查问卷18份，回收18份，有效问卷为18份，有效率为100%。一级指标的权重系数如下表3。

表3 各个一级指标权重系数

如比赛成绩指标的加权均数的计算为：所有专家选中9分的次数为4次，选中10分的次数为14次，即加权均数为(9×4+10×14) / (4+14) = 9.78。如果没有缺失值，那么所有专家对每一个指标的评分得分乘以次数相加后，都除以18即可(共18个专家)。其它指标的加权均数依次为7.50、9.00、7.00、8.89。所以一级指标加权均数之和为：9.78+7.50+9.00+7.00+8.89=42.17。

二级指标的权重系数的确定也采用同样的方法。如比赛成绩的二级指标分别是最终成绩、阶段性大赛成绩、训练成绩。其权重的计算如表4所示。

表4 比赛成绩的各个二级指标权重系数

注：本指标总的加权均数的和为22.5。

所以最终成绩指标的权重系数等于一级指标比赛成绩指标的权重系数(0.23)乘以二级指标下最终成绩指标的权重系数(0.44)计算得：0.23×0.44≈0.10，依次计算出阶段性大赛成绩指标的权重系数为0.07，训练成绩指标的权重系数为0.06。

3.2 因子分析法确定权重

3.2.1 适用条件

因子分析法这是一种客观确定指标权重的方法，是根据指标自身的作用和影响确定权重的方法，还有主成分分析法、聚类分析法、判别分析法等。适用于采用SPSS统计分析软件对指标体系中各变量进行因子分析，并根据因子的贡献率确定指标的权重。它要求问卷发放的量比较大，而且原则上越大越好。一般为指标变量数与样本量比例为1：5为宜，实际理想的样本量应该为指标变量数的10～25倍。5～10倍之间略显不足，但一般都能得到较好的结果(吴明隆，2010)[8]。应用的目的是一般是编制量表或建立某个研究项目的评价指标体系。

3.2.2 因子分析法确定指标权重的过程与方法

因子分析是检验评价量表信度与效度的常用手段。其特点是在现有数据的基础上，依靠观测变量之间的相关，提取较少因素就能反映大部分原始数据信息，从而起到简化变量、分清因素结构的作用。它的缺点是不能估计因变量和自变量的测量误差。本研究主要探讨采用因子分析法确定指标的权重。在根据一定的专业理论知识，建立了指标体系，编制问卷，并发放回收问卷。采用SPSS统计软件对指标体系进行因子分析。

使用因子分析的方法对参加评价的所有指标进行分析，首先要判断各个指标之间是否适合进行因子分析。KMO值与Bartlett球度检验是SPSS统计软件提供的判断各变量是否适合进行因子分析的统计检验方法。KMO在0-1之间，其值越接近1，表明变量间共同因素越多，越适合进行因子分析。因子分析要求变量间有较强的相关性，Bartlett球度检验是检验变量间相关系数矩阵是否为单位矩阵的方法，其检验结果呈现出统计显著性(如P≤ .05)，则说明变量间的相关系数矩阵不是单位矩阵，变量间有较强的相关性，适合进行因子分析，反之则不适合进行因子分析。其次，先将所有指标进行因子分析，根据因子提取的要求(如提取特征值>1)和一定的专业理论知识，采用方差最大正交旋转，提取特征值>1的因子；接着计算每个因子的权重，即用该因子的贡献率除以所有特征值大于1的因子的累计贡献率。最后，计算每个因子中各个指标的权重，方法是在因子内按照指标载荷的大小，按比例分割因子权重作为指标权重(任弘，2004)[4]。

3.2.3 应用举例

现将数据在SPSS统计软件进行录入，使用如下命令：Analyze / Data Reduction / Factor，进入因子分析的操作，具体步骤和说明详见有关SPSS统计软件的参考书。本例采用的数据资料是前人有关体质四因素(形态、机能、素质、社会适应)中各指标权重系数的计算，见表5。

本例在研究中根据特征值大于1提取原则，共提取五个公因子。表5中的权重系数是指该因子的载荷(方差贡献率)占特征值大于1的所有因子总载荷(累计贡献率)的百分比。如表5中因子1的权重等于第一因子的方差贡献率16.595除以5个因子累计方差贡献率65.509，即为0.25。其他四个因子照此法计算出的权重系数分别为0.246、0.194、0.155、0.151。

表5 体质四因素因子分析结果

数据引自2004年任弘博士论文《体质研究中人体适应能力的理论与实证研究》。

在表6中列出了5个因子中每个因子中包括的二级指标，每个因子的权重再由该因子中包含的指标的因子载荷按比例分担。具体计算方法：如因子1包括仰卧起坐、纵跳两个二级指标，其中仰卧起坐的权重系数为它在两个指标载荷之和中占的比例，再乘以因子1的权重系数0.25。即：[0.966 / (0.966+0.962)]×0.25=0.125259，调整为0.125。其他各个二级指标的权重系数我们以此法依次计算出来。

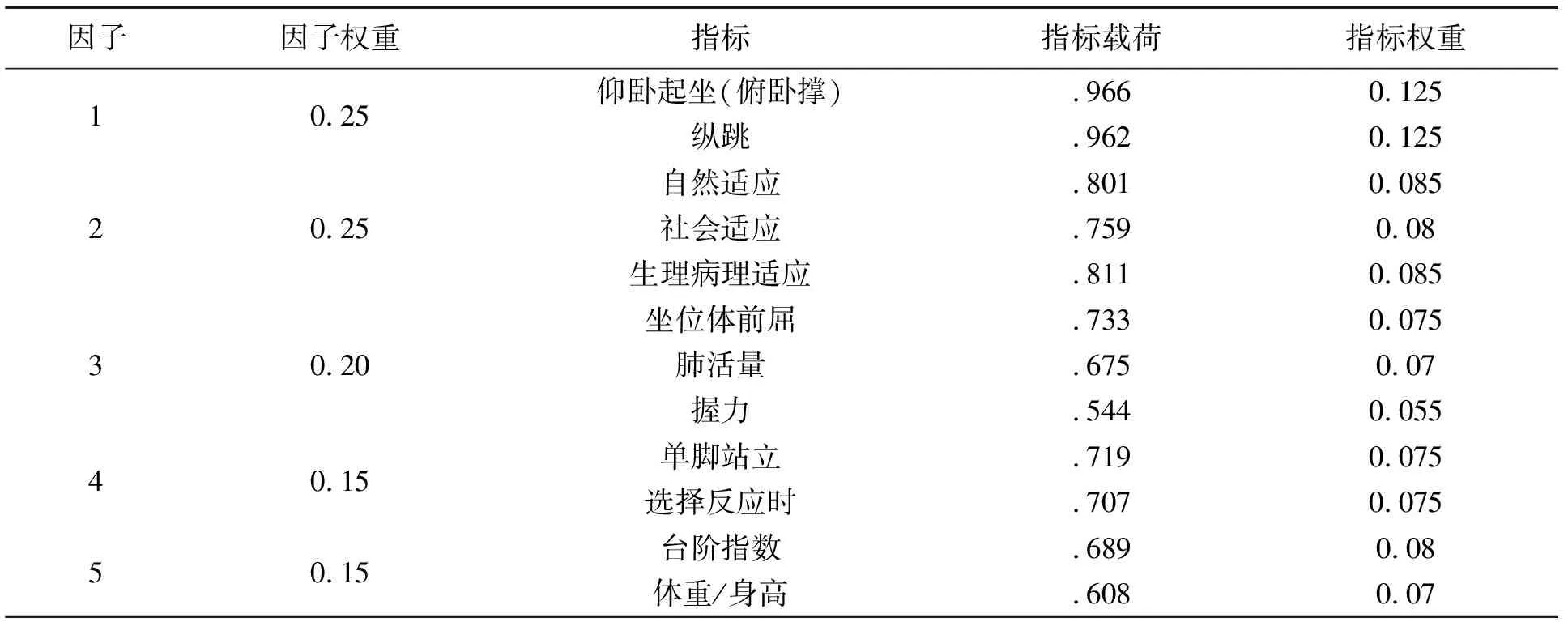
表6 体质综合评价指标权重(40岁以下)

数据引自2004年任弘博士论文《体质研究中人体适应能力的理论与实证研究》。

3.3 层次分析法确定权重

3.3.1 层次分析法的理论与适用条件

层次分析法简称AHP法，实际上也是一种定性与定量分析相结合的多准则确定权重的决策方法。对于复杂的综合评价问题，将专家的意见汇总后利用数学模型对实际问题进行抽象和简化。目的是为回避评估者和决策者的选择与判断所起的决定性作用。基本思想是把复杂的问题分解为各个组成因素，将这些因素按支配关系分组，使之形成有序的递阶层次结构。通过两两比较，确定层次中各因素的相对重要性，然后综合判断，将决策因素的相对重要性进行排序。此方法是先将研究的问题分为目标层、准则层、方案层三个层次。相对于目标层求出准则层各要素的相对权重。然后相对于准则层求出方案层各要素的相对权重。最后以准则层各要素的相对权重为权，求出方案层相对于目标层的组合权重。这个组合权重就是各个方案相对于总目标的重要程度。

适用条件是问卷的发放对象都是有关研究领域的权威或专家。层次分析法涉及到高等数学知识，要求使用者有一定的数学基础。另外这种方法涉及到的计算量较大，所以专家组的成员一般由10人左右组成为宜，不易过多。

3.3.2 层次分析法的确定指标权重的过程与方法

本研究采用层次分析法确定权重的方法是美国著名的运筹学专家萨迪(T.L.Satty)等人在研究人们的选择、判断与决策的思维规律的基础上提出来的。具体操作步骤如下(高洪军，2008；余涛，2009；方强，2010)[9,6,10]：

(1) 明确问题，建立层次结构

用层次分析法作系统分析，对决策问题要有明确的认识，根据问题的性质，各因素间的相互关系和隶属关系，把问题层次化，以形成一个多层次的分析结构模型同一层次的各元素作为准则对其下一层元素起支配作用，同时其本身亦受上一层元素的支配，这种自上而下的支配关系形成了一个递阶层次结构。

(2) 建立两两判断矩阵

在确定的递阶层次结构中，每一个元素和该元素支配的下一层元素构成一个子区域，对于子区域内的各元素采用专家调查法来构建若干个判断矩阵(每位专家给出一个判断矩阵)。设上一层次的元素A作为准则，对下一层次的元素C1、C2、Cn有联系，则判断矩阵A如表7。

表7 判别矩阵

然后把属于每一层次的评判因素逐对的进行比较判断，通常使用1～9比例标度法将相对重要性的逻辑判断数量化，其值由专家根据自己的综合判断结果给出。按其因素的重要程度，引用1～9的比例标度(见表8)。

表8 判断矩阵标度及其含义

(3) 计算判断矩阵的最大特征根和对应的特征向量可采用下面近似计算方法:

(4) 对判断矩阵计算最大特征根λmax。

一致性指标C.I.的值越小，表明判断矩阵的一致性越高：当C.I. < 0.1时，可认为判断矩阵是满意的，否则就需要对判断矩阵进行调整。

(6) 根据判断矩阵的阶数n，查找相应的平均随机一致性指标RI。对于1-10阶判断矩阵，RI值如表9所示。

表9 平均随机一致性指标

3.3.3 应用举例

以下是篮球运动员体能的评价指标体系，见表10。本例属于多人单准则下权重的计算，利用Excel软件分别求出每位专家判断矩阵的权重向量。

第一步，建立层次分析结构模型。

篮球运动员的体能分为形态、机能与素质三个维度。

表10 篮球运动员体能权重研究层次分析结构表

上表中形态指标包括身高、体重、上肢长、手长、肩宽等5个指标。素质指标包括100m、握力、3000m、反应时、坐位体前屈等5个指标。机能指标包括肺活量1个指标。目标层即篮球运动员体能；准则层为形态、机能与素质三个二级指标。方案层为所有的11个三级指标。

第二步，构造判别矩阵。目标层与准则层间权重的确定方法：选择4位专家，经过专家调查得到目标层与准则层间判别矩阵如下(见表11)：

表11 目标层判断矩阵表

第三步，相对权重的求法。根据每位专家的判别矩阵，求出最大特征根及其对应的特征向量，该向量的各分量就是判断距阵各要素相对于上一层次某要素的相对权重。可以用和积法或方根法求解，在此用方根法。

第一位专家的判别矩阵如下表12所示。其他专家的判别矩阵略。

表12 专家1的目标层判断矩阵

①计算第一位专家判别矩阵中的每一行元素的乘积的方根。

②对每一个方根作归一化处理，即为所求的权重系数。

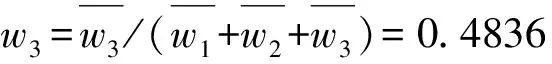
③计算λmax。

λ1= (1×0.1667 +1/3×0.3487 +1/2×0.4836) / 0.1667 = 3.1477

λ2= (3×0.1667+1×0.3487+1/2×0.4836) / 0.3487 = 3.127617

λ3= (2×0.1667 +2×0.3487 +1×0.4836) / 0.4836 = 3.131514

λmax=(λ1+λ2+λ3) / 3 = (3.1477+3.127617+3.131514) /3 = 3.1356

⑤计算C.R.。查平均随机一致性指标RI表得RI=0.58。

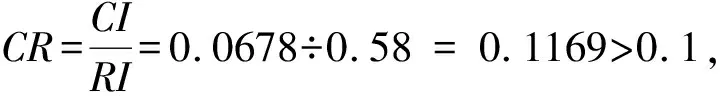
由以上①②③④⑤步依次计算其他三位专家的判断矩阵的权重系数及为

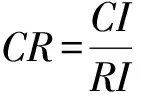
这里λl为满足一致性检验条件的专家的权，这里取λ1=λ2=λ3=1/3，经计算得：

所以准则层形态、机能、素质的权重系数分别为：

W1=0.1469/0.9947=0.1477,W2=0.4240/0.9947=0.4261,W3=0.4240/0.9947=0.4261

此例中，方案层的指标的权重系数的确定方法同准则层，这里略过。对于评价时选的专家人数较多，且指标较多，计算量较大，可以采用EXCEL软件进行编程计算。

4 结语

本研究介绍了体育综合评价中三种常用的指标权重的方法有主观评价法、因子分析法及层次分析法。通过对三种综合评价确定权重的方法的适用条件、理论基础及操作过程进行了梳理，并用实例进行演示，希望能够为体育科学研究者提供一些理论经验与捷径。但目前层次分析法可以通过EXCEL软件编制模板程序来实现。因子分析法对样本量要求比较高，要求样本量比较大，要求研究者能够熟悉因子分析法的基本原理并熟练掌握一些统计软件，例如SPSS。 实际科学研究中研究者要分清以上三种方法的使用条件，三种方法还可结合使用。层次分析法是一种定性与定量相结合的方法，一定程度上能够克服个人的主观判断的偏差。虽然在应用中难度比较大，但不失是一种好的方法，建议研究者们要大胆尝试。

参考文献：

[1] 赵书祥. 我国体育领域中综合评价理论与方法及实证的研究[D]. 北京体育大学博士学位论文, 2008.

[2] 祁国鹰, 徐明. 在体育统计简明教程[M]. 北京体育大学出版社, 2006.

[3] 徐明欣, 高斌, 李瑞年, 鞠传进. 我国普通高校体育课程评估方案的研制与实践[J]. 体育科学, 2000, 20(2): 15-18.

[4] 任弘. 体质研究中人体适应能力的理论与实证研究[D]. 北京体育大学博士学位论文, 2004.

[5] 赵书祥. 体质综合评价中层次分析法的应用研究[J]. 北京体育大学学报, 2007, 30(7): 938-940.

[6] 方强. 高等学校体育教学质量评价体系的层次分析研究[J]. 广州体育学院学报, 2010, 30(3): 109-112.

[7] 于万清. 阳光体育背景下学生体育成绩量化研究—运用层次分析法对体育成绩评定[J]. 体育科技文献通报, 2010, 18(4): 82-83.

[8] 吴明隆. 问卷统计分析实务—SPSS操作与应用[M]. 重庆大学出版社, 2010.

[9] 高洪军. 自学考试助学组织评价体系的研究及评价系统的实现[D]. 北体工业大学硕士学位论文, 2008.

[10] 余涛. 我国群众体育发展评价研究[D]. 北体体育大学博士学位论文, 2009.